Практикум по механике и молекулярной физике

С другой стороны, из рис. 3 видно, что угол α можно записать через длину дуги x и радиус ℓ: α = x/ℓ, т. е. сила, возвращающая маятник в положение

равновесия, является квазиупругой: Рt = − mgA x , где k = mgA – коэффици-

ент квазиупругой силы. Второй закон Ньютона в этом случае будет иметь

Период колебаний математического маятника при малых углах отклонения не зависит от амплитуды колебания и от его массы, а определяется длиной маятника и ускорением свободного падения g.

Физический маятник

Физическим маятником называется абсолютно твердое тело, которое может совершать колебания под действием силы тяжести

0вокруг горизонтальной оси О, перпендикулярной плоско-

асти рисунка и не проходящей через его центр тяжести. На рис.4 изображено сечение физического маятника плос-

Скостью, перпендикулярной к его оси вращения О и прохо-

них сил. В нашем случае момент внешних сил обусловлен действием силы тяжести. Очевидно, что на каждый элемент массы mi маятника действует сила тяжести mig, создающая определенный момент относительно оси О. Сумма моментов этих силы равна моменту равнодействующей сил тяжести, которая приложена к центру тяжести маятника (точка С).

Докажем, что маятник, выведенный из положения равновесия на малый угол φ, будет совершать гармонические колебания. Для этого равнодействующую сил тяжести P = mg разложим на две составляющие, одна из которых P2 уравновешивается реакцией опоры, а под действием другой составляющей P1=Psinφ маятник приходит в движение. Обозначим расстояние от точки подвеса О до центра тяжести С через a. Тогда уравнение дви-

21

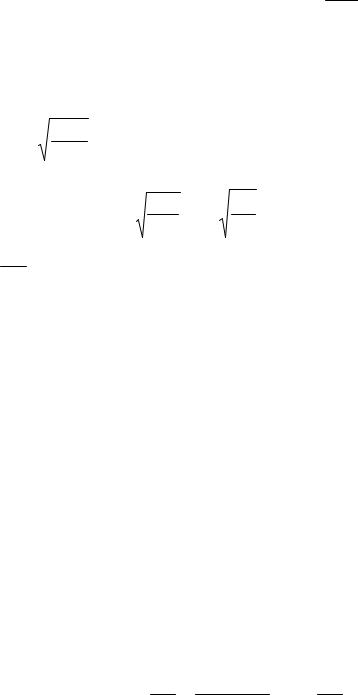
Знак минус показывает, что сила P1 направлена к положению равновесия и

приводит к уменьшению угла отклонения φ. Так как β = d 2ϕ , а для малых dt 2

углов φ можно принять sinφ ≈ φ, то уравнение (10) будет иметь вид:

Частным решением этого дифференциального уравнения является уравнение

Величина Anp = maJ называется приведенной длиной физического маятни-

ка, это есть длина эквивалентного математического маятника, имеющего тот же период колебаний, что и данный физический маятник.

Физическим маятником также можно воспользоваться для определения ускорения свободного падения.

Любой физический маятник обладает свойством сопряженности, которое заключается в том, что в нем можно найти такие две точки, что при последовательном подвешивании маятника за ту или иную из них период колебаний его остается одним и тем же. Расстояние между этими точками определяет собой приведенную длину физического маятника.

Разновидностью физического маятника является оборотный маятник, который обладает свойством сопряженности центра качания и точки подвеса. Центром качания называется точка, находящаяся на расстоянии приведенной длины Anp от оси вращения. Приведенная длина всегда

больше величины a (см. рис. 4), т. е. центр качания всегда лежит ниже центра тяжести. Действительно, по теореме Штейнера момент инерции маятника относительно оси вращения равен J = Jo + ma2, где Jo – момент инерции маятника относительно оси, проходящей через центр тяжести. Тогда

приведенная длина ℓпр равна Anp = maJ = J0 +mama2 = a + maJo , т. е. Anp > a.

22

23

тат фиксируется на световом индикаторе. Схема управления осуществляет синхронное включение и выключение счетчика колебаний и секундомера. Зная число колебаний маятника и время, за которое они совершаются, можно определить период колебания маятника.

Выполнение работы

Проверьте, заземлен ли прибор. Включите сетевой шнур в сеть 220 В. Нажмите выключатель «СЕТЬ», при этом индикаторы измерителя показывают нуль и горит лампочка фотоэлектрического датчика. Прибор готов к работе.

Упражнение 1. Изучение законов колебательного движения

математического маятника и определение ускорения свободного падения

Нижний кронштейн вместе с фотоэлектрическим датчиком установите на отметке 50 см. Затяните винт, фиксируя фотоэлектрический датчик

визбранном положении. С помощью верхнего кронштейна поместите над датчиком математический маятник. Вращая винт на верхнем кронштейне, опустите шарик математического маятника до нижнего кронштейна, обращая внимание на то, чтобы черта на шарике была продолжением черты на корпусе фотоэлектрического датчика. Таким образом устанавливается длина математического маятника.

1.Проверка зависимости периода колебаний от его длины и амплитуды.

Для этого приведите маятник в колебательное движение, отклонив шарик от положения равновесия на 4–50. Нажмите кнопку «СБРОС». После отсчета измерителем 15–20 полных колебаний нажмите кнопку «СТОП». Определите период колебаний маятника по формуле T = t/n, где n – число колебаний, t – показание электронного секундомера. Измерения периода проводятся не менее трех раз. Изменяя длину маятника на 2–3 см

водну и другую сторону, проведите аналогичные измерения для других длин маятника. Данные измерений занесите в таблицу.

1

2

3

Cp

Не меняя длину маятника, определите периоды колебания маятника при разных амплитудах колебания А. Измерения также проводятся не ме-

24

нее трех раз для каждой амплитуды. Составьте таблицу, аналогичную предыдущей, и все данные занесите в эту таблицу.

Сделайте вывод, как зависит период колебаний математического маятника от его длины и амплитуды.

2. Используя имеющиеся усредненные данные для периода колебаний, по формуле (8) определите ускорение свободного падения g.

С целью оценки погрешности g выведите формулу для расчета абсолютной и относительной ошибки измерения и определите их ( l = 2мм, аТберется из эксперимента).

Упражнение 2. Определение ускорения свободного падения при помощи оборотного маятника

Положение на стержне физического маятника чечевиц и одной из опорных призм П2 указывается преподавателем. Крепление всех деталей на стержне следует производить очень тщательно, добиваясь, чтобы зажимные винты входили в канавки на стержне. При изменении положения чечевицы или опорных призм маятник надо снять с кронштейна, положить на стол и провести перемещения чечевиц или призмы.

Установите маятник на призму П1. Нижний кронштейн вместе с фотоэлектрическим датчиком переместите таким образом, чтобы стержень маятника пересекал оптическую ось датчика.

Отклоните маятник на 4–50 от положения равновесия и дайте возможность ему совершать колебания.

Нажмите кнопку «СБРОС» и после подсчета измерителем 15–20 полных колебаний нажмите кнопку «СТОП». Определите период колебаний оборотного маятника по формуле T1 = t1/n1, где n1 – число колебаний, t1 – показание электронного секундомера. Результаты заносятся в таблицу.

Затем маятник снимается с кронштейна, переворачивается и устанавливается на призму П2. Снова определяются значения n2, t2 и вычисляются значения T2. Измеряется и вносится в таблицу расстояние l между опорными призмами маятника.

Переместите призму П2 на соседнее деление в таком направлении, чтобы Т2 по своему значению приближался к значению Т1. Определяют и заносят в таблицу новые значения l, n2, t2, T2. Эти измерения повторяются до 4–5 раз, пока значение периода Т1 не попадет в «вилку» полученных значений Т2 (значения Т1 и Т2 не должны отличаться более чем 0,5 %).

При равенстве Т1 и Т2 определите приведенную длину маятника как расстояние между ребрами опорных призм и вычислите ускорение свободного падения по формуле (12).

25

Используя соотношение (13), можно, зная lпр, массу маятника (m = 2,6 кг), определить момент инерции маятника J и величину а, т. е. положение центра тяжести мятника (см. рис. 4).

РАБОТА № 2–2 ПРОВЕРКА ЗАКОНОВ КОЛЕБАНИЯ МАТЕМАТИЧЕСКОГО

МАЯТНИКА И ОПРЕДЕЛЕНИЕ УСКОРЕНИЯ СВОБОДНОГО ПАДЕНИЯ

Приборы и принадлежности: математический маятник, секундомер, штангенциркуль.

Описание установки

В качестве математического маятника в работе используется тяжелый металлический шарик 1, подвешенный на длинной тонкой нити (рис. 6).

Длина нити может меняться путем перемещения крепящего кронштейна 2 вдоль нити и измеряется по шкале 3, амплитуда колебаний маятника измеряется по шкале 4.

При выполнении данной работы необходимо определение длины математического маятника и его периода колебаний.

Длина математического маятника ℓ находится как сумма длины нити ℓ1 от положения кронштейна до шарика (измерения проводятся по милли-

Для проверки этого соотношения кронштейном 2 установите длину маятника 140–150 см и определите его период колебаний. Затем, передвигая кронштейн, уменьшите длину маятника вдвое и опять определите период колебаний. Измерения проводятся не менее трех раз и данные заносятся в таблицу.

26

3. ЗАТУХАЮЩИЕ КОЛЕБАНИЯ

Простейшим видом колебательного движения является гармоническое, которое совершается по закону синуса или косинуса. Оно возникает в том случае, если на тело, выведенное из положения равновесия, непрерывно действует сила, направленная всегда к положению равновесия, а по величине пропорциональная смещению этого тела от положения равновесия.

Колебательные движения системы имеют особенно простой характер в случае малых колебаний, когда мало смещение системы от положения равновесия. Примером простейших колебательных систем может слу-

Рассмотрим такое колебательное движение шарика, подвешенного на упругой пружине (рис. 1).

После отклонения шарика от положения равновесия он будет совершать гармонические колебания. Если деформация пружины невелика, то можно считать справедливым закон Гука и записать выражение для возвращающей в равновесие шарик силы F в виде: F = −kx , (1) где k – коэффициент пропорциональности, зависящий от упругих свойств пружины, x – смещение относительного положения равновесия. Знак минус показывает, что сила направлена к положению равновесия, т. е. имеет знак, обратный знаку x. Под влиянием этой силы предоставленный самому

себе шарик начнет двигаться, приобретая скорость V = dxdt . При его движе-

нии возникает сила трения Fтр, направленная противоположно скорости. В первом приближении ее можно считать пропорциональной скорости ша-

где r – коэффициент пропорциональности, называемый коэффициентом сопротивления (коэффициент трения).

Если масса шарика невелика (это дает возможность пренебречь силой тяжести по сравнению с возникающими упругими силами), то второй

28

В формулу (5) входят два множителя, зависящие от времени. Один cos t – периодическая функция времени, другой е- t убывает с течением времени. Тогда, если коэффициент сопротивления мал, то величину А = А0е– t можно рассматривать как амплитуду, которая с течением времени уменьшается по экспоненциальному закону, окончательно решение уравнения зату-

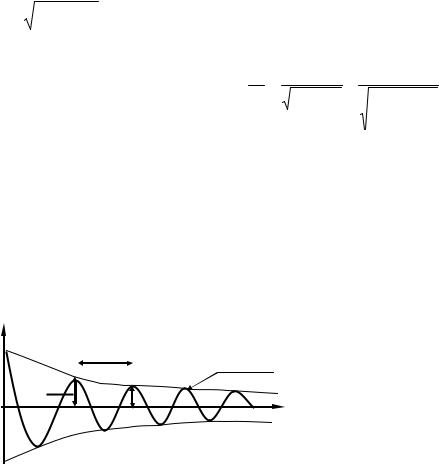
Затухающие колебания представляют собой непериодические колебания, так как в них никогда не повторяются, например, максимальные значения смещения, скорости и

A = A0 e−δ t , выражающей закон убывания амплитуды колебаний, можно

показать, что отношение амплитуд, отделенных друг относительно друга интервалом в один период Т, остается постоянным в течение всего процесса затухания.

Итак, возьмем отношение двух амплитуд Аn и An+1 (см. рис. 2)

29

Величина D называется декрементом затухания. Чем больше декремент затухания, тем скорее уменьшается амплитуда. Чаще затухающие колебания характеризуются логарифмическим декрементом затухания :

Таким образом, для характеристики затухающих колебаний вводятся две величины: коэффициент затухания и логарифмический декремент затухания . Поясним их физический смысл.

Обозначим через промежуток времени, за который амплитуда ко-

Следовательно, коэффициент затухания есть физическая величина обратная промежутку времени , в течение которого амплитуда убывает в е раз. Величина называется временем релаксации.

Если, например, = 102 с, то это значит, что амплитуда колебаний убывает в е раз за время 102 с.

Пусть n – число колебаний, после которых амплитуда уменьшается в е раз. Тогда = nT и = Т= 1/ = 1/n.

Следовательно, логарифмический декремент затухания есть физическая величина, обратная числу колебаний n, по истечении которого амплитуда убывает в е раз.

Если, например, = 0,01, то это значит, что амплитуда колебаний убывает в е раз по истечении 100 колебаний.

РАБОТА № 3–1

ОПРЕДЕЛЕНИЕ ЛОГАРИФМИЧЕСКОГО ДЕКРЕМЕНТА ЗАТУХАНИЯ И КОЭФФИЦИЕНТА ЗАТУХАНИЯ КРУТИЛЬНЫХ КОЛЕБАНИЙ

Приборы и принадлежности: прибор для наблюдения упругих (крутильных) колебаний, секундомер.

30