
Практикум по механике и молекулярной физике
.pdf
|
|
n |
|
квадратичная абсолютная погрешность: |
Nквадр = ± |
∑( Ni )2 |
. |
i=1 |
|||
|
|
n(n −1) |
|
(4)
Здесь n – число измерений, а ∑(∆Ni)2 есть сумма квадратов абсолютных ошибок отдельных измерений.
Погрешности косвенных измерений
В большинстве случаев для получения результата надо произвести ряд прямых измерений других величин, связанных между собой определенными формулами. Зная погрешности, допущенные при измерениях этих величин, входящих в формулу для определения искомого результата, необходимо определить и погрешность самого результата.
Для нахождения абсолютных и относительных погрешностей косвенных измерений удобно пользоваться следующими правилами:
1)средние абсолютные ошибки можно находить по правилам дифференцирования, заменив значок дифференцирования (d) значком ошибки ( ). Знаки (+ или –) при этом надо выбирать так, чтобы абсолютная ошибка была max;
2)относительную погрешность результата можно найти следующим образом: логарифмируем исходное выражение, а затем его дифференцируем, заменяя в конечном итоге значки d на значок . Знаки + и – опять-таки выбираем таким образом, чтобы абсолютная величина относительной ошибки была бы максимальной.
Проиллюстрируем нахождение N и Е косвенных измерений.
1. Измеряемая величина находится по формуле N = 2ab2 . Величины c3
а, b и c находятся прямыми измерениями, и для них рассчитываются а, b, c. Необходимо найти абсолютную и относительную ошибки величины N.
Найдем N. Для этого вначале продифференцируем все выражение для N:
dN = |
2ab2d(c3 ) + c3d(2ab2 ) |
= |
2ab3 3c2dc + c3 (2da b2 + 2a 2bdb) |
= |
||||||||||||
|
|
(c3 )2 |
|
|
|
|
|
c6 |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
затем |
|||
|
ab2 |
|
b2 |
|
ab |
|
|
|
|
|
|
|
|
|
||
= 6 |
dc + 2 |
da + 4 |
db; |
|
|
|
|
|
|
|
|
|||||
c4 |
c3 |
c3 |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
значки дифференцирования заменяем на |
и получаем абсолютную |
|||||||||||||||
ошибку N: |
|
|
|
|
|
b2 |
|
|
|
|
|
|
||||
|
|
|
|
|
ΔΝ = 2 |
a + 4 |
ab |
b + 6 |
ab |
c. |
|
|||||
|
|
|
|
|
c3 |
c3 |
c4 |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Теперь найдем Е, исходя из значения |
N. |
|
|
|
||||||||||||
11

Ε = |
ΔΝ |
= 2b 2 ac 3 |
+ 4 ab bc 3 |
+ 6 |
ab 2 c |
c 3 = |
a |
+ 2 |
b |
+ 3 |
c . |
|
Ν |
c 4 2 ab 2 |
a |
b |
|||||||||
|
c 3 2 ab 2 |
c 3 2 ab 2 |
|
|
|
|
c |
Из этого примера видно, что здесь проще было бы найти относительную ошибку, а затем абсолютную. Скажем сразу, что во всех тех случаях, когда искомая величина есть произведение и дробь величин, измеренных непосредственно на опыте, удобнее и легче находить в первую очередь относительную погрешность, а затем абсолютную. В самом деле:
N = |
2ab2 |
, lnN = ln2 + lna + 2lnb – 3lnc, после дифференцирования, |
||||
|
c3 |
|
|
|
|
|
замены значков дифференцирования на |
и изменения знаков так, чтобы |
|||||
ошибка была максимальная, получаем E = |
ΔΝ = |
a + 2 |
b |
+ 3 c . |
||
|
|
|
Ν |
a |
b |
c |
А теперь, если нужно, можно найти и |
N, зная, что |
N = Е · N. |
||||
|
1.3. ИЗУЧЕНИЕ ИЗМЕРИТЕЛЬНЫХ ПРИБОРОВ |
|||||
|
|
Нониусы |
|
|
|
|
Часто при измерении длины какого-либо тела длина его не уклады- |
||||||
вается в целое число делений масштаба. Для того чтобы можно было поручиться при линейных измерениях и за десятые доли масштаба (а иногда и за сотые), пользуются нониусом.
Нониус – это дополнительная шкала к основному масштабу (линейному или круговому), позволяющая повысить точность измерения с дан-
ным масштабом в 10, 20 и более число раз. |
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
Нониусы бывают линейные и круговые, прямые и обратные, нерас- |
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
тянутые и растянутые. |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Линейный |
нониус пред- |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ставляет собой небольшую ли- |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
нейку (шкалу), скользящую вдоль |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
большей |
масштабной |
линейки |
|
0 |
10 |
20 |
|
30 |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
(рис.2). Как видно из рис.1, 10 де- |
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
лений нониуса |
соответствуют 9 |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
делениям |
основного |
масштаба. |
|
В случае прямого нерастянутого нониуса, который мы рассматриваем, одно деление нониуса короче одного деления масштаба на величину , которая называется точностью нониуса. Точность нониуса является разностью длин делений основного масштаба и нониуса и легко может быть определена, если мы знаем число делений нониуса n и длину наименьшего деления масштаба αm
= 1n αm .
12

Длина отрезка, измеряемая при помощи нониуса, будет равна числу целых делений масштаба до нуля нониуса плюс точность нониуса, умно-
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
женная на номер его деления, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
совпадающего с некоторым де- |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
лением масштаба. На рис. 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
длина тела равна13,3, так как |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
совпадает с делениями мас- |
|
|
0 |
10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
20 |
30 |
|
|
|
|
|
|
|
штаба 3-е деление нониуса. |
|||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 3 |
|
Погрешность, |
которая |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
может возникнуть |
при таком |
методе отсчета, будет обуславливаться неточным совпадение деления нониуса с одним из делений масштаба, и величина ее не будет превышать,
очевидно, |
1 |
. Таким образом, можно сказать, что погрешность нониуса |
|
2 |
|||
|
|
равна половине его точности.
Чтобы легче было заметить, какое деление нониуса совпадает с ка- ким-либо делением основной шкалы, на практике делают нониусы растянутыми. Прямой растянутый нониус получится, если длина одного деления нониуса будет короче не одного наименьшего деления масштаба (как мы полагали до сих пор), а двух, трех и т. д. наименьших делений его.
Точность нониуса в этом случае определяется по той же формуле. Круговой нониус в принципе ничем не отличается от линейного.
Он представляет собой небольшую дуговую линейку, скользящую вдоль круга лимба, разделенного на градусы или на доли градуса (рис. 4). Точность кругового нониуса обычно выражается в минутах. Часто круговые
нониусы в приборах, в которых не- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
обходимо отсчитать углы в обоих |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
направлениях (по часовой стрелке |
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
или против нее), состоят из двух |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10 |
|
|
|
|
|
|
|
|||
|
|
|
|
|
20 |
30 |
|
|
||||||
совершенно одинаковых шкал, рас- |
|
|
|
|
|
|
||||||||
170 |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
положенныхпообестороныотнуля. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Очень часто в круговых но- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
175 |
|
|
|
|
|
|
|
|
|
|
||
ниусах αм = 0,5о = 30 минут , а n рав- |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
185 |
||||
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
180 |
|
||||||||
но 15 или 30, в таком случае точ- |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|||
ность нониуса, соответственно равна |
|
|
|
|
|
Рис. 4 |
|
|
|
|
||||
двум минутам или одной минуте. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
В лабораторной практике для измерения длин, площадей и объемов наиболее распространенными приборами являются штангенциркуль и микрометр.
13

|
Штангенциркуль |
4 |
1 |
|
0 |
1 |
2 |
15 |
|
|||
|
|
0.1 |
|
|
|
мм |
5 |
|
|
|
|
|
|
2 |
|
|
3 |
Рис. 5 |
|
Штангенциркуль (рис. 5) служит для линейных измерений, не требующих высокой точности.
Отсчетным приспособлением у всех конструкций штангенциркулей служит основная масштабная шкала штанги 1, цена деления которой 1 мм, и линейный нониус на подвижной рамке 2. Он представляет собой небольшую линейку, скользящую вдоль основного масштаба. На этой линейке нанесена маленькая шкала, состоящая из m делений.
При нулевом показании инструмента нуль нониуса совпадает с нулевым штрихом основной шкалы. При измерении подвижная рамка с нониусом смещается и предмет зажимается губками 3 штангенциркуля. Так как цена деления нониуса не равна цене деления масштаба, то обязательно найдется на нем такое деление, которое будет ближе всего подходить к ка- кому-то делению масштаба.
Правило отсчета можно сформулировать следующим образом: длина предмета, измеряемого при помощи нониуса, равна числу целых делений масштаба плюс точность нониуса, умноженная на номер деления нониуса, совпадающего с некоторым делением масштаба. В лабораторной практике обычно используются штангенциркули с точностью 0,1 и 0,05 мм, которая указывается на приборе.
Для измерения внутренних размеров тел служат обычно верхние заостренные ножки 4. Если же штангенциркуль не имеет верхних ножек, то измерение внутренних размеров производится теми же ножками, которые служат для обмера наружных размеров тела; в этом случае необходимо учитывать толщину ножек штангенциркуля, которая указывается на самом инструменте. Некоторые штангенциркули снабжаются линейкой 5, служащей для измерения глубин.
В лабораторной практике широко используются также круговые нониусы в различных приборах для измерения углов.
14

Микрометр
Микрометр (рис. 6) служит для измерений диаметров проволок, небольших толщин пластинок и т.п. Он имеет вид тисков и при измерении пред-
мет |
зажимается |
между |
|
|
|
|
неподвижным стержнем 1 |
|
|
|
|
||
и |
подвижным |
торцом |
|
|
0 |
|
микрометрического винта |
1 |
2 |
4 |
3 |
||
2. |
Микровинт вращают, |
|||||
держась за трещетку 3. На |
|
0.01 мм |
5 |
|
||
стержне микровинта ук- |
|
Рис.6 |
|
|||
реплен барабан 4, с нане- |
|
0 – |
|
|||
|
|
|
||||
сенной на нем |
шкалой, |
|
|
|
|
|
имеющей 50 делений. Отсчет ведется по горизонтальной шкале 5 и по шкале барабана. Ход винта (поступательное перемещение барабана и стержня 2 при совершении одного оборота винта) равен 0,5 мм. Это означает, что цена деления барабана 0,01 мм. Следует обратить внимание, что выше основной миллиметровой шкалы имеется дополнительная линейная шкала, смещенная относительноосновнойна0,5 мм.
Прежде чем пользоваться микрометром, необходимо убедиться, что микрометр исправлен – нули его шкал совпадают. Измеряемый предмет помещают между стержнем
|
|
|
|
|
|
|
|
|
|
20 |
|
|
|
|
|
|
|
|
|
|
|
20 |
1 и винтом 2. Затем, вращая |
|
|
|
|
|
|
|
|
|
|
|
15 |
|
|
|
|
|
|
|
|
|
|
|
15 |
винт за головку 3, доводят |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
0 5 |
|
|
|
|
|
0 5 |
|
|
|
его до |
соприкосновения с |
||||||||||||
|
|
|
10 |
|
|
|
|
10 |
предметом. Момент зажатия |
|||||||||||||||
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
Рис. 7 |
|
|
фиксируется треском. После |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
этого |
треска дальнейшее |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
вращение головки 3 бесполезно, а барабана 4 недопустимо. Отсчет производят по шкалам: миллиметры по основной линейной шкале, доли миллиметра по шкале на барабане. При отсчете необходимо учитывать, появилась ли половинка деления верхней шкалы после последнего перед краем барабана деления нижней основной шкалы или нет. На рис. 7 крупным планом показаны шкалы микрометра. Как видно из рис. 7 (слева), когда край барабана перешел нижнюю риску, соответствующую 6,00 мм, а риска верхней шкалы не видна, то длина измеряемого предмета равна 6,15 мм. Когда же край барабана перешел верхнюю риску (рис. 7, справа), соответствующую 6,50 мм, то длина измеряемого предмета равна 6,65 мм. Нетрудно понять, что цена деления барабана, равная 0,01 мм, и является точностью прибора, которая указывается на микрометре.
15
1.4. ОПРЕДЕЛЕНИЕ ПЛОТНОСТИ ТВЕРДЫХ ТЕЛ, ИМЕЮЩИХ ПРАВИЛЬНУЮ ГЕОМЕТРИЧЕСКУЮ ФОРМУ
Приборы и принадлежности: исследуемые тела, штангенциркуль или микрометр, технические весы с разновесами.
Плотностью вещества ρ называется физическая величина, измеряе-
мая отношением массы вещества к его объему, т. е. |
ρ = |
m |
, |
|
|||
|
V |
|
|
где m – масса вещества, V – его объем.
Для определения ρ надо знать эти две величины. Масса твердого тела находится при помощи рычажных весов. Объем тела правильной геометрической формы вычисляется по формулам геометрии. Измерение линейных размеров тела производится при помощи штангенциркуля или микрометра.
Рассмотрим два примера.
1. Тело имеет форму прямоугольного параллелепипеда. Пусть a, b, c – длины его ребер. Тогда объем параллелепипеда будет равен V = a · d · c. Измерение линейных размеров тела производится с помощью штангенциркуля, точность которого 0,05 мм. Масса тела находится на технических весах, точность которых определяется наименьшим разновесом, который используется при взвешивании (обычно m = 10 мг = 0,01 г).
Пусть линейные размеры тела определяются по три раза в разных местах, а масса – один раз. Как следует из теории погрешностей, при небольшом числе измерений можно ограничиться нахождением средней арифметической абсолютной ошибки измерений и соответствующей ей относительной ошибки. Данные измерений рекомендуется записать в табл. 1.
Таблица 1
№ |
а, |
| a|, |
b, |
| b|, |
с, |
| с|, |
m, |
m, |
п/п |
мм |
мм |
мм |
мм |
мм |
мм |
г |
|
|
|
|
|
|
|
|
|
г |
1 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
Ср |
|
|
|
|
|
|
|
|
Расчет ρср производится по средним значениям измеряемых величин,
т.е. по формуле |
ρср = |
m |
. |
|
|||
|
|
abc |
|
Все вычисления необходимо проводить в одной системе единиц: в ед. СИ (кг, м) или в системе СГС (г, см).
Оценим теперь погрешности измерений. В нашем случае проще сначала вычислить относительную ошибку измерений, а затем уже абсолютную. Тогда, пользуясь табл. 1, находим
|
ρ |
|
m |
|
a |
|
b |
|
c |
||
Ε = ± |
|
100 % = ± |
m |
+ |
a |
+ |
b |
+ |
c |
100 %. |
|
ρср |
|||||||||||
|
|
|
|
|
|
||||||
16

Откуда |
ρ = |
|
Ε |
ρср. |
|
100 |
|||||
|
|
|
|||
После вычисления ошибок необходимо сопоставить приборные ошибки и расчетную среднюю абсолютную ошибку результата. Результат эксперимента следует записать в виде ρ = (ρср ± ρ) г/см3.
2. Тело имеет форму цилиндра, диаметр которого равен d, а высота Н.
Тогда объем тела равен V = 14 πd 2H. Измерение линейных размеров ци-
линдра производится с помощью микрометра, точность которого 0,01 мм. Масса цилиндра определяется на технических весах с точностью 0,01 г. Пусть масса тела определяется один раз, а размеры не менее пяти раз. Для такого количества измерений, как следует из теории погрешностей, целесообразнее вычислить средние квадратичные ошибки измерений σ. Данные измерений записываются в табл. 2.
|
|
|
|
|
|
|
Таблица 2 |
|
№ d, |
| d|, |
( d)2, |
Н, |
| Н|, |
( Н)2, |
m, |
m, |
|
п/п мм |
мм |
мм |
мм |
мм |
мм |
г |
г |
|
1
2
3
4
5
Ср
Расчет ρср производится по средним значениям измеряемых величин
по формуле |
ρср = |
4m |
. |
|
|||
|
|
πd 2H |
|
Средние квадратичные ошибки σd и σН находятся по формуле (5). В данном примере, как и в предыдущем, удобнее сначала вычислить относительную ошибку результата. Пользуясь табл. 2, находим
Ε = ± |
σρ |
100 % = ± |
|
m 2 |
|
σ |
2 |
σ |
|
2 |
|
ρср |
|
|
+ 2 |
|
d |
+ |
|
H |
100 %. |
||
|
|
|
m |
|
d |
|
H |
|
|||
Отсюда средняя квадратичная погрешность измерения плотности
σρ = 100Ε ρср.
Окончательный результат вычисления плотности тела записывается в виде ρ = (ρср ± σρ) г/см3.
17
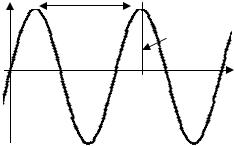
2. ГАРМОНИЧЕСКИЕ КОЛЕБАНИЯ
Колебательным движением (колебанием) называется процесс, при котором система, многократно отклоняясь от своего состояния равновесия, каждый раз вновь возвращается к нему. Если этот процесс совершается через равные промежутки времени, то колебание называется периодиче-
ским.
Несмотря на большое разнообразие колебательных процессов как по физической природе, так и по степени сложности, все они совершаются по некоторым общим закономерностям и могут быть сведены к совокупности простейших периодических колебаний, называемых гармоническими, которые совершаются по закону синуса (или косинуса).
Предположим, что они описываются законом
x = Αcosφ = Αcos(ωt +φ0 ), |
(1) |
здесь x – смещение (отклонение) колеблющейся системы от положения равновесия; А – амплитуда, т. е. максимальное смещение от положения равновесия, (ωt +ϕ0 ) – фаза колебаний. Физический смысл фазы в том,
что она определяет смещение х в данный момент времени, φо – начальная фаза колебания (при t = 0); t – время колебаний; ω – круговая частота (или угловая скорость) колебаний. ω связана с частотой колебания ν и периодом колебания Т:
ω = 2πν = |
2π |
, |
(2) |
Τ |
|||
Т – период - время одного полного колебания. |
φо = 0, то график зависи- |
||
Если в уравнении (1) положить начальную фазу |
|||
мости смещения х от времени или график гармонического колебания будет
x |
|
иметь вид, представленный на рис. 1. |
T |
Систему, закон движения которой |
|
|
A |
имеет вид (1), называют одномерным |
|
классическим гармоническим осцилля- |
|
|
|
|
|
|
тором. |
|
t |
Хорошо известным примером гар- |
|
монического осциллятора является тело |
|
|
Рис.1 |
(шарик), подвешенное на упругой пружи- |
|
не. По закону Гука при растяжении или |
сжатии пружины возникает противодействующая сила, пропорциональная растяжению или сжатию х, т. е. тело будет совершать гармонические колебания под действием силы упругости пружины F = –kx. Однако гармонические колебания возникают под действием не только упругих, но и других сил, по природе не упругих, но для которых остается справедливым закон F = –kx. Такие силы получили на-
звание квазиупругих.
18

Как известно, движение системы под действием силы описывается вторым законом Ньютона: ma = F, где a – ускорение колеблющейся системы. Для гармонических колебаний F = –kx. Тогда второй закон Ньютона будет иметь вид неполного дифференциального уравнения второго порядка
m |
d 2 x |
+ kx = 0 , |
(3) |
|
dt |
2 |
|||
|
|
|
|
|
или уравнение движения классического осциллятора, где a = ddt2 2x .
Решением данного уравнения (3) является выражение (1), что нетрудно проверить, дифференцируя дважды (1) по времени и подставляя в уравнение (3). При этом получим, что
ω2 = |
k |
. |
(4) |
|
|||
|
m |
|
|
Для упрощения записи в дальнейшем можно положить начальную фа-
зу нулю (φо = 0), тогда уравнение (1) будет иметь вид
(1΄)
x = Αcosωt.
Скорость гармонически колеблющегося тела можно найти, дифференцируя по времени уравнение (1΄):
x,v,a |
|
|
|
|
dx |
= −Αωsinωt |
||||
|
|
|
|
υ = dt |
||||||
|
|
|
|
|
|
|
|
π |
|
|
|
|
|
x |
или υ = Αωcos ωt + |
2 |
. |
|
|||
|
|
|
(5) |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
v t |
Видно, что |
скорость |
при |
||||
|
|
|
гармонических |
колебаниях |
тоже |
|||||
|
|
|
a |
изменяется |
по |
гармоническому |
||||
|
|
|
закону, но |
опережает смещение |
||||||
|
|
|
Рис.2 |
по фазе на |
π (по времени на Т/4). |
|||||
|
|
|
Рис. 2 |
|||||||
Ускорение |
|
|
2 |
|
|
|
|
|
||
тела при гармонических |
колебаниях |
равно: |
||||||||
a = dυ |
= d 2 x |
= d |
(Αωsinωt), или |
|
|
|
|
|
|
|
dt |
dt 2 |
dt |
a = −Αω2 cosωt = +Αω2 cos(ωt +π). |
|
|
|
|
|||
|
|
|
|
|
|
(6) |
||||
Сравнение этого выражения (6) с (1) показывает, что ускорение и смещение находятся в противофазе (рис. 2). Это означает, что в тот момент, когда смещение достигает наибольшего положительного значения, ускорение достигает наибольшего по величине отрицательного значения, и наоборот.
19

Кинетическая энергия осциллятора при гармоническом колебании
с учетом (4) и (5) имеет вид |
|
|
mυ2 |
|
1 |
2 2 |
|
2 |
|
Εk |
= |
|
= |
|
mA ω |
sin |
|
ωt. |
|
2 |
2 |
|
|||||||
|
|
|
|
|
|
|
|
Потенциальная энергия: Εn = 12 kx2 = 12 kA2 cos2 ωt , а так как «k»
связано с собственной частотой колебания осциллятора (ω2 = mk ), то
Εn = 12ω2mA2 cos2 ωt.
Полная энергия гармонического осциллятора в процессе колебаний не меняется. Действительно:
Ε = Εk + Εn = 12 mA2ω2 (sin2 ωt + cos2 ωt)= 12 mA2ω2 = const.
Из последнего выражения видно, что полная механическая энергия осциллятора пропорциональна квадрату амплитуды и не зависит от времени. Кинетическая и потенциальная энергии изменяются по гармоническо-
му закону, как sin2 (ωt) и cos2 (ωt), но когда одна из них увеличивается, дру-
гая уменьшается. Это означает, что процесс колебаний связан с периодическим переходом энергии из потенциальной в кинетическую и обратно.
Рассмотрим некоторые из классических гармонических осцилляторов.
|
|
|
|
Математический маятник |
||
|
Математическим маятником называют систему, состоящую из неве- |
|||||
|
|
|
|
сомой и нерастяжимой нити, на которой подвешен ша- |
||
|
|
|
|
|||
|
α |
|
рик, |
масса шарика сосредоточена в одной точке |
||
|
|
(рис. 3). В положении равновесия на шарик действуют |
||||
NG |
A |
две силы: сила тяжести P=mg и сила натяжения нити |
||||
N – равные по величине и направленные в противопо- |
||||||
|
|
N |
||||
|
|
ложные стороны. |
||||
|
|
|
G |
|
Если маятник отклонить от положения равнове- |
|
|
Pt |
сия на небольшой угол α, то он начнет совершать коле- |
||||
|
||||||
|
αPn |
бания в вертикальной плоскости под действием состав- |
||||
P |
P |
ляющей силы тяжести Pt, которую называют тангенци- |
||||
альной составляющей (нормальная составляющая силы |
||||||
|
||||||
|
Рис.3 |
|
тяжести Pn будет уравновешиваться силой натяжения |
|||
|
|
|
|
нити N). |
||
|
Из рис. 3 видно, |
что тангенциальная составляющая силы тяжести |
||||
Ρt =−Ρsinα.
Знак минус показывает, что сила, вызывающая колебательное движение, направлена в сторону уменьшения угла α. Если угол α мал, то синус можно
заменить самим углом, тогда |
Ρt = −Ρα = −mgα . |
20
