spez_fiz_pr_zachita

электронов на аноде ФЭУ, которое вызвано одним электроном, испущенным фотокатодом, и дисперсию числа электронов, испускаемых фотокатодом за время t :

малых размеров, используемых без световодов, так как в этом случае членом Dt 2 можно пренебречь.

Вреальных случаях при оценке минимального значения D t

необходимо принимать N 110, так как из-за термоэмиссии имеется высокий фон импульсов с малыми амплитудами. Лучшее разрешающее время схем

совпадений с жидкими сцинтилляторами: 3 10–9 с. Вдвое больше у стильбена: 6 10–9 с, для кристалла NaI(Tl)– около 2 10–8 с. Эти данные

приведены для схем совпадений, работающих в области 100% – ной эффективности регистрации совпадений.

4.4.3. Энергетическое разрешение сцинтилляционного детектора

Амплитуда импульса пропорциональна числу электронов, приходящих на анод ФЭУ и равных Ne Np M, где N – среднее число фотонов,

испущенных сцинтиллятором; M – средний коэффициент усиления ФЭУ; p – вероятность того, что фотон, образовавшийся в сцинтилляторе, приведет

к появлению электрона на первом диноде ФЭУ. Последняя величина – это произведение вероятности фотона попасть на фотокатод на вероятность фотоэффекта на фотокатоде и на вероятность попадания электрона на первый динод ФЭУ. Относительная среднеквадратическая флуктуация в импульсе

испускаемых сцинтиллятором, равно 1N . Величину Dp / p2 вряд ли можно

оценить, поскольку она зависит от конкретных свойств ФЭУ и сцинтиллятора. Особенно от того, насколько одинакова конверсионная эффективность фотокатода в различных точках, насколько однороден кристалл (его прозрачность, его конверсионная эффективность), какова однородность оптического контакта сцинтиллятора с фотокатодом и т. д.

Величину Dp / p2 для каждого конкретного сцинтилляционного счетчика можно измерить.

121

Дисперсия коэффициента усиления ФЭУ здесь определена как дисперсия в числе электронов на аноде ФЭУ, если на его первый динод попадает заданное (не флуктуирующее) число электронов (в данном случае pN ).

Расчеты показывают, что основной вклад в дисперсию числа электронов на аноде вносит дисперсия коэффициента вторичной электронной эмиссии на первых динодах, а дисперсия коэффициента усиления ФЭУ оказывается обратно пропорциональной числу электронов, попадающих на первый динод, и не зависит от числа динодов в фотоумножителе.

Окончательное выражение для относительного значения дисперсии амплитуд импульсов имеет следующий вид [2]:

где – коэффициент вторичной электронной эмиссии с динодов.

Первый член в (4.27) обратно пропорционален числу фотонов, возникающих в сцинтилляторе, т. е. энергии излучения, а второй не зависит от энергии излучения и определяется качеством изготовления сцинтиллятора и фотоумножителя. Распределение амплитуд импульсов около своего среднего значения хорошо аппроксимируется распределением Гаусса. Тогда, полагая, что энергия частицы и амплитуда импульса пропорциональны, выразим энергетическое разрешение сцинтилляционного счетчика через

эффективность сцинтиллятора.

Полученная зависимость энергетического разрешения сцинтилляционных счетчиков от энергии заряженных частиц достаточно хорошо подтверждается на опыте. Оценим постоянную C1 . Для кристаллов

NaI(Tl) на создание одного фотона сцинтилляций заряженная частица (электрон) затрачивает 30–50 эВ. Величина p по порядку величин составляет

около 5% (конверсионная эффективность фотокатода не лучше 0,1 потери света; потери электронов при сборе на первый динод). Принимая e 5,

122

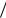
При таких значениях C1 и % 2 энергетическое разрешение 3 для

энергии 1 МэВ приблизительно равно 4,5%. При регистрации -квантов зависимость энергетического разрешения от энергии в виде (4.28) имеет место в области энергий около 2 МэВ.

В области больших энергий -квантов флуктуации в числе фотонов люминесценции и флуктуации в коэффициенте усиления умножителя не имеют уже основного значения. Здесь становится существенной утечка излучения из кристалла: при регистрации -квантов электроны могут образовываться вблизи поверхности кристалла и выходить из него, теряя часть своей энергии вне сцинтиллятора. Это приведет к появлению импульсов меньших амплитуд. Такой эффект имеет особенно большое значение в тех случаях, когда фотон поглощается в кристалле в результате многих последовательных взаимодействий с электронами. Этот эффект оказывается существенным даже для кристаллов больших размеров. Например, в кристалле диаметром 125 и длиной 200 мм при энергии-квантов около 4 МэВ вклад в энергетическое разрешение за счет утечек

излучения из кристалла составляет около 5%, а при энергии -квантов, равной 10 МэВ, этот вклад равен примерно 8%. В то же время статистические флуктуации для указанных энергий равны, соответственно, 4 и 2%.

Энергетическое разрешение сцинтилляционных счетчиков не является хорошим. С лучшим по световыходу кристаллом NaI(Tl) можно получать

3 14% при энергиях электронов около 100–150 кэВ. В области энергий

выше 2–4 МэВ лучшее полученное энергетическое разрешение составляет около 4–5%. Для других кристаллов энергетическое разрешение будет хуже, поскольку их конверсионная эффективность меньше. В стильбене, например, при регистрации протонов энергетическое разрешение можно оценить, используя соотношение 3 ~ 15Ep %, где Ep энергия протонов, МэВ.

4.4.4. Эффективность сцинтилляционных детекторов

Эффективность сцинтилляционных детекторов можно рассчитать сравнительно просто и с достаточной для многих приложений точностью. Рассмотрим сцинтиллятор в виде цилиндра, на продолжении оси которого находится источник моноэнергетических -квантов. По определению эффективность есть отношение числа зарегистрированных импульсов к числу частиц, попавших в детектор. Число квантов, попавших в кристалл,

испускаемых источником изотропно по всем направлениям. Вероятность регистрации фотона, движущегося в направлении − , равна Ι1 exp( l(−) ))ϑ,

где l – путь -кванта в сцинтилляторе; ) полный линейный коэффициент

123

ослабления -квантов в веществе сцинтиллятора. Очевидно, что для указанной геометрии эффективность запишется в следующем виде:

Полученное значение эффективности справедливо в том случае, если регистрируется каждый импульс, появившийся в результате взаимодействия

-кванта с кристаллом. Если у регистрирующей системы есть порог срабатывания VB , то эффективность регистрации [2]

произвести всегда достаточно уверенно, поскольку величины ) E известны

с погрешностью 1 1,5%, а размеры кристалла и его плотность также можно определить с необходимой точностью, то расчет функции отклика G(E,V )

оказывается сложной задачей. Расчет эффективности регистрации нейтронов по ядрам отдачи водорода проводится аналогичным образом.

При регистрации -квантов сцинтилляционными счетчиками с неорганическими кристаллами часто используют понятие эффективности по фотопику. Функция G(E,V ) для

где Ф – эффективность по фотопику.

124

Эффективность регистрации сцинтилляционным счетчиком -квантов и нейтронов довольно большая. Так, для кристалла NaI(Tl) диаметром и

такого кристалла при энергии -квантов 4,5 МэВ составляет примерно 0,2, а при энергии 0,66 МэВ – около 0,5. Эффективность регистрации нейтронов с энергией 10 МэВ кристаллом стильбена высотой и диаметром 30 мм составляет около 10%. При энергии нейтронов 1 МэВ d 0,45.

5. ИЗЛУЧЕНИЕ ВАВИЛОВА—ЧЕРЕНКОВА

Свечение чистых жидкостей под действием ионизирующих излучений наблюдалось со времен Марии и Пьера Кюри. Однако до опытов П.А. Черенкова не было доказательств того, что это свечение имеет природу,

опыты с тушением заведомо флуоресцирующих растворов, проводившиеся параллельно и в тех же условиях, во всех случаях обнаруживали заметный эффект тушения. Эти результаты исключали возможность люминесценции. В 1936 г. было открыто новое наиболее замечательное свойство излучения – его направленность. Оказалось, что свечение обладает резко выраженной пространственной асимметрией. Оно испускается только вперед в

направлении, образующем некоторый угол с направлением возбуждающего пучка частиц. Открытие этого фундаментального свойства

излучения позволило установить истинную природу излучения и создать его теорию. Согласно теории, созданной И.М. Франком и И.Е. Таммом, свечение интерпретируется как свечение равномерно движущихся в среде электронов со скоростью, превышающей фазовую скорость света в этой среде. Интересно отметить, что на возможность излучения частицей, движущейся со сверхсветовой скоростью, обратил внимание еще Кельвин. Несколько позднее (в 1904 г.) Зоммерфельд рассмотрел гипотетический случай движения электрона в вакууме со сверхсветовой скоростью. Появление теории относительности, согласно которой частицы не могут двигаться со скоростью большей скорости света, сделало выводы Зоммерфельда мало актуальными. Однако при движении в веществе возможны скорости,

125

превышающие скорость света. Это связано с тем, что скорость распространения света в среде с показателем преломления n равна v cn .

Так, как для видимого света n 1, то скорость распространения световых волн в среде будет меньше скорости света в пустоте.

Простое качественное рассмотрение позволяет получить условия возникновения излучения и установить некоторые его весьма важные свойства. Пусть электрон равномерно движется в среде в направлении оси x

выходящих из различных точек траектории электрона в некотором направлении − , не приводила к их взаимному гашению, необходимо время прохождения частицей пути АБ приравнять времени прохождения светом пути АВ. Поскольку АБ>АВ, то v cn . Отсюда получаем [1]

В направлении, определяемом выражением (5.1), будет происходить излучение.

Отметим, что формула (5.1) для угла излучения была получена еще в 1888 г. английским физиком и математиком О. Хэвисайдом. Это излучение имеет в акустике свой аналог в виде ударной волны, образуемой летящим со сверхзвуковой скоростью телом. Двумерным аналогом является хорошо всем известная носовая волна корабля.

Из равенства (5.1), которое является одним из важнейших результатов теории И.М. Франка и И.Е. Тамма, следует, что излучение возможно только при условии n 1, т. е. если скорость частицы v cn . Таким образом,

равенство n 1 определяет энергетический порог излучения. Значение

энергии E этого порога зависит от коэффициента преломления n . Поскольку в условия, определяющие этот порог, входит непосредственно не энергия, а скорость частицы , то очевидно, что E зависит от массы частицы. В табл.

5.1 приведены значения пороговой энергии E для электронов, -мезонов и протонов при трех значениях n .

126

Обычно показатель преломления среды n для синих лучей больше, чем

красного к фиолетовому (рис. 5.2). Такие фотографии были получены на пучке протонов 660 МэВ на ускорителе в Объединенном институте ядерных исследований.

Потери энергии на излучение Вавилова – Черенкова не зависят от заряда атомов среды. При большой скорости частицы потери энергии достигают практически постоянного значения. Практически достигает постоянного значения и угол, под которым направлено излучение. Поэтому для ультрарелятивистских частиц использовать излучение Вавилова – Черенкова для идентификации частиц затруднительно. С этой точки зрения значительный интерес представляет переходное излучение.

5.1. Длительность световой вспышки

Длительность вспышки излучения Вавилова–Черенкова практически определяется временем пролета частицы через радиатор. Для излучателя длиной несколько сантиметров и скорости частицы, близкой к скорости света, длительность вспышки составляет 10–10 с. Минимальная длительность вспышки определяется дисперсией. В недиспергирующей среде волновой фронт имеет бесконечно малую толщину, и поэтому длительность световой вспышки в этом случае бесконечно мала. Если среда обладает дисперсией, то угол излучения будет разным для различных длин волн.

Тогда длительность светового импульса t , измеряемая вдоль прямой,

параллельной направлению движения частицы на расстоянии r от ее траектории, определяется выражением [1]

127

числа электронов составляют в этом случае 2%. При этом полагаем, что

N 1 N .

Как известно, в тонком сцинтилляторе (потеря энергии частицей мала по сравнению с кинетической энергией частицы) распределение потерь энергии описывается распределением Ландау. Полная ширина этого распределения на половине высоты составляет около 20–30% наиболее вероятного значения потерь энергии. Это связано с тем, что значительная часть света, испускаемого в сцинтилляторе, возбуждается %-электронами малой энергии.

В черенковском детекторе условия оказываются совершенно иными, так как большая часть света испускается непосредственно самой частицей. Некоторая часть черенковского излучения может быть обусловлена

небольшим числом %-электронов с энергиями, превышающими пороговую, например, 260 кэВ в случае воды. Доля света, обусловленная %-электронами, зависит, во-первых, от того, насколько энергия частицы превышает пороговую энергию, во-вторых, от максимально передаваемой энергии E и, в-третьих, от энергетического распределения %-электронов.

Энергетическое разрешение черенковского детектора определяется, в основном, флуктуациями числа фотоэлектронов и для рассмотренного примера (радиатор толщиной 2 см) составляет 14%, т. е. примерно в 2 раза меньше полуширины распределения, полученного для сцинтиллятора той же толщины.

Заметим, что относительная интенсивность черенковского и тормозного излучений составляет для электрона с энергией 100 МэВ, движущегося через

5.4. Детекторы излучения Вавилова – Черенкова

Детектор состоит из радиатора, в котором генерируется излучение, и приемника, который это излучение регистрирует. Излучение возникает в радиаторе только при условии, что скорость заряженной частицы, проходящей через радиатор, превышает фазовую скорость света в

веществе радиатора. На этом основан принцип действия пороговых детекторов. Сигнал на выходе детектора возникает только в том случае, если скорость заряженной частицы превышает определенную величину. Пороговый детектор можно сконструировать и таким образом, что он будет регистрировать частицы, энергия которых не превышает определенного значения.

Другой класс детекторов излучения Вавилова – Черенкова позволяет не только регистрировать частицы, скорость которых лежит в определенных пределах, но и непосредственно определять эту скорость. В этом случае детектор является спектрометром частиц высокой энергии.

129

Таким образом, существуют два типа детекторов: пороговые детекторы и детекторы с фокусировкой, которые позволяют определять скорость частицы.

Подчеркнем основные свойства излучения Вавилова – Черенкова. Излучение наблюдается у всех чистых прозрачных материалов; излучение поляризовано с преимущественной ориентацией вектора напряженности электрического поля вдоль направления первичного пучка частиц (лежит в плоскости, проходящей через луч и направление движения частицы). В отличие от люминесценции не наблюдается ни температурного, ни примесного тушения излучения.

Условие, при котором возникает излучение Вавилова – Черенкова,n 1 начинает выполняться для электронов уже при энергиях порядка

105 эВ, а для протона при энергиях порядка 1010 эВ.

Детекторы, основанные на регистрации этого излучения, позволяют определять непосредственно скорость частицы.

Излучение Вавилова – Черенкова в радиаторе небольшой длины или с изменяющимся по длине показателем преломления сопровождается переходным изучением, возникающим при прохождении частицы через

преломления среды n соотношением cos− 1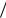 n . Число испускаемых

фотонов на единицы пути частицы, например, в плексигласе в видимой области света для частиц со скоростью, близкой к скорости света, составляет около 250 фотонов на 1 см.

5.4.1. Радиаторы

Для регистрации частиц не очень большой скорости в качестве радиатора применяют жидкости и твердые тела. Коэффициент преломления радиатора зависит от природы вещества. Так, например, показатель преломления может изменяться от n 1,276 (фторохимикат FC-75, C8 F16O ) до

используемые в качестве радиаторов черенковского излучения, и их

значению скорости частицы.

С помощью пороговых детекторов с жидкими и твердыми радиаторами можно разделить между собой частицы со скоростью 0,95 0,96

( -мезоны с импульсом до 0,5 ГэВ/с, )-мезоны с импульсом до 0,35 ГэВ/с, K-мезоны с импульсом до 1,6 ГэВ/с, протоны до 3,0 ГэВ/с).

130