matmod

Л.2. Типы математических моделей

Пример 3 (продолжение). Проверка закона сохранения энергии E.

Дискретная модель. 0 6 i 6 N, u0(t) = uN (t) = 0.

Л.2. Типы математических моделей

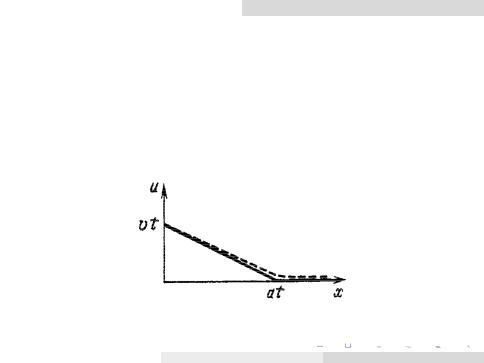
Пример 3 (продолжение).

Отличия между решениями уравнений в непрерывной и дискретной моделях.

Скорость распространения любых деформаций согласно непрерывной модели равна a

Для дискретной модели влияние внешних воздействий распространяется с формально бесконечной скоростью

Адекватность можно восстановить, если пренебречь слишком малыми значениями смещений: u(xi ) 6 ǫ → u(xi ) ≡ 0.

2014 32 / 74

Л.3. Типы математических моделей

Лекция 3. Типы математических моделей (продолжение)

Л.3. Типы математических моделей

Линейные и нелинейные модели

Линейная зависимость одной величины от другой – это пропорциональность их приращений, т.е.

z = ax + by + c z = a x + b y

Типичные линейные зависимости между физическими величинами – закон Гука,

закон Ома, закон теплопрового расширения и т.д.

Понятие линейной модели.

Применяется для моделей объектов, рассматриваемых как преобразователи (операторы), для которых каждому входу соответствует некоторый выход.

Пусть начала отсчета входа и выхода выбраны так, что нулевому входу отвечает нулевой выход.

Модель называется линейной, если в ней выполнен принцип суперпозиции (наложения), т. е. при сложении входов складываются и выходы, а при умножении входа на любое число выход умножается на то же число. Если этот принцип не выполнен, модель называется нелинейной.

Л.3. Типы математических моделей

Линейные модели обычно описываются линейными неоднородными уравнениями – алгебраическими, дифференциальными и т.д., в которых неоднородный член отвечает входу, а решение выходу. Примеры:

1. Краевая задача о малом поперечном прогибе стержня с шарнирно закрепленными концами x = a, x = b:

q(x) – вход, y(x) – выход.

2. Задача Коши для осциллятора под действием внешней силы F (t) (вход). Координата x – выход.

mx¨ + kx = F (t) (0 6 t < ∞), x(0) = 0, x˙ (0) = 0.

Л.3. Типы математических моделей

Линеаризация

Линеаризация – приближенная замена нелинейной модели на линейную.

Применяется в случаях:

1)эксперимент показывает, что отклонение от линейности в рассматриваемых диапазонах изменения переменных невелико и несущественно,

2)эти диапазоны малы и мы заменяем приращения переменных на их дифференциалы, отбрасывая члены высшего порядка малости.

(Во втором случае применяется также линейное интерполирование.)

Л.3. Типы математических моделей

Линеаризация. Примеры.

1.Пусть величины х, у, z связаны уравнением

x3 + xy + e2z + 5 = 0.

y3 − xz

Это уравнение удовлетворяется при x = 2, y = −1, z = 0. Пусть ξ, η, ζ – малые изменения x, y, z соответствено:

x = 2 + ξ, y = −1 + η, z = ζ.

Требуется найти линейное соотношение между ξ, η, ζ, справедливое с точностью до членов высшего порядка малости.

Продифференцируем обе части исходного уравнения:

и подставим x = 2, y = −1, z = 0 и dx = ξ, dy = η, dz = ζ (пренебрегаем величинами высшего порядка малости).

2014 37 / 74

Л.3. Типы математических моделей

(11ξ + 2η)(−1) − 6(3η − 2ζ) + 2ζ = 0 11ξ + 20η − 14ζ = 0.

Или в переменных x, y, z:

11x + 20y − 14z = 0.

Геометрический смысл: получили уравнение касательной плоскости к заданной поверхности в точке (x, y, z) = (2, −1, 0).

Л.3. Типы математических моделей

2. Рассмотрим дифференциальное уравнение

y′′ + (1 + y2) sin y′ + y = 1,

имеющее частное решение y0(x) = 1.

Задача получить линеаризованное уравнение для функции η(x), определеящей близкое решение y(x) = 1 + η(x).

Варьируем исходное уравнение и подставляем y = y0 = 1, δy = η:

(δy)′′ + 2y(δy) sin y′ + (1 + y2)(cos y′)(δy)′ + δy = 0,

η′′ + 2η′ + η = 0.

Л.3. Типы математических моделей

На последовательной линеаризации основан один из самых эффективных методов приближенного решения нелинейных уравнений различных типов – метод Ньютона.