Формула Байеса

Теорема 4. Пусть имеется полная группа несовместных событий B₁, B₂,..., B_n. Известны Р(B_i), . Событие А, для которого Р(А)>0 может произойти толь с одним из. Известны Р(А/B_i), . Тогда апостериорная вероятность Р(B_k/А) определяется формулой:

(2)

Доказательство По определению

На основе формулы полной вероятности получаем:

.‹

2. - формула Байеса.

Вероятности Р(B_k) называются априорными (a priori - до опыта) вероятностями; Р(B_k/А) - апостериорными (a posteriori - после опыта). События B_i часто называют гипотезами.

Пример. В урне лежит шар неизвестного цвета, с равной вероятностью белый или черный. В урну кладут белый шар, перемешивают и вынимают наудачу шар. Он оказался белым. Какова вероятность того, что в урне остался белый шар?

Решение: Обозначим событие А={вынут белый шар}

B₁={в урне остался белый шар}={в урне был белый шар}; B₂={в урне черный шар}. Очевидно, Р(B₁)=Р(B₂)=1/2; P(A/ B₁)=1; P(A/ B₂)=1/2. Необходимо найти Р(B₁/А).

По формуле Байеса:

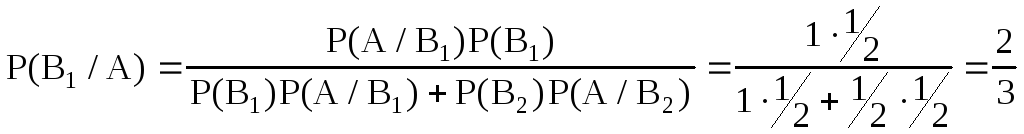
Ответ: Р(B₁/А)=2/3

Таким образом, апостериорная вероятность события B₁ существенно больше априорной.

Схема независимых испытаний Бернулли

Независимость опытов (испытаний, экспериментов). Пусть имеется два произвольных опыта G₁ и G₂ и соответствующие им вероятностные пространства: <W₁,F₁,P₁> и <W₂,F₂,P₂> . Рассмотрим составной эксперимент G с вероятностным пространством <W,F,P>, где W=W₁´W₂ - прямое произведение W₁ и W₂, а s-алгебра F порождена событиями ВÎF, где В=В₁´В₂, В₁ÎF₁, В₂ÎF₂ .

Замечание: Прямым произведением W=W₁´W₂ называется множество W, элементами которого являются упорядоченные пары элементов пространств W₁ и W₂; т.е. если W₁={w_i⁽¹⁾}, a W₂={w_j⁽²⁾}, то W={w_i⁽¹⁾ w_j⁽²⁾}, где w_i⁽¹⁾ и w_j⁽²⁾ - любой элемент W₁ и W₂ соответственно.

Испытания G₁ и G₂ независимы, если для любых В=В₁´В₂ выполняется равенство: Р(В)=Р₁(В₁)Р₂(В₂).

Последовательность n испытаний G₁, G₂,..., G_n называется независимой, если Р(В)=Р₁(В₁)Р₂(В₂)...Р_n(В_n), где В=В₁´В₂´...´В_n , В_к ÎF_к, <W_к,F_к,P_к> - вероятностное пространство, соответствующее k-му эксперименту.

Схема независимых испытаний Бернулли: Рассмотрим n независимых испытаний G_k, . В каждом из этих испытаний событие А может появиться с одной и той же вероятностью Р(А)=р и не появиться с вероятностью q=1-p=P(). Такая совокупность испытаний называется схемой независимых испытаний Бернулли.

Вероятность появления в n испытаниях события А m раз. Рассмотрим вероятностное пространство отдельного эксперимента <W_к,F_к,P_к>, где W_к={A, } - пространство элементарных событий. Совокупность n - испытаний представляет собой составной эксперимент с вероятностным пространством <W,F,P>, где W={w_i}- пространство элементарных событий, элементы которого w_i -и упорядоченные совокупности из n элементов А и :

, , и т.д.

Так как эксперименты независимы, то

Р (АА...А)=рр...р=рⁿ – вероятность того, что n раз появится событие А.

Р(...)=qq...q=qⁿ – вероятность того, что А не появится ни разу.

–вероятность того, что в первых m событиях А появится, а в (n-m) - не появится.

Нас интересует вероятность события В_m={А появилось в n испытаниях m раз} независимо от порядка их появления:

Обозначим Р(В_м)=Р_n(m), тогда

(1)

где .

Формула (1) - формула Бернулли или биномиальный закон распределения вероятностей.

События В_m , m=0..n составляют полную группу несовместных событий, поэтому

(2)

Вероятность того, что событие А при n испытаниях произойдет не более k раз:

(3)

Вероятность того, что при n испытаниях событие А произойдет более k раз

(4)

Пример. В группе 10 студентов. Вероятность присутствия на занятии каждого из них Р(А)=0.9. Какова вероятность того, что на занятиях будет присутствовать 7 человек?

Решение:

P₁₀(m>7)=P₁₀(8)+P₁₀(9)+P₁₀(10)

P₁₀(8)==0.194

P₁₀(9)= =0.387

P₁₀(10)= =0.349

P₁₀(m>7)=0.194+0.387+0.349=0.932