Аксиомы вероятности (аксиомы Колмогорова)

• Аксиома №1 (аксиома неотрицательности):

Р(А)³0 , для любого АÎ E или АÎF

Каждому событию А соответствует неотрицательное число – вероятность этого события.

• Аксиома №2 (аксиома нормировки):

Р(W)=1.

Вероятность достоверного события равна 1.

• Аксиома №3 (аксиома аддитивности):

Если заданы события такие, что при i¹j, то

(*)

Вероятность суммы несовместных событий равна сумме вероятностей.

Замечание: Функции множеств, обладающие свойством (*) при n< называются аддитивными мерами, а при n= – счетно-аддитивными мерами.

Определение: Вероятность – неотрицательная, нормированная к единице мера, заданная на измеримом пространстве событий, характеризующая степень возможности появления событий.

Соответствие между событиями и их вероятностями называется распределением вероятности.

Таким образом, Р(А), как функция множеств АÎF, (E) определяет распределение вероятностей на F,( E). Пространство элементарных событий W с заданной на нем алгеброй E (или s-алгеброй F) подмножеств и определенной на E (F) вероятностью Р называется вероятностным пространством.

Обозначение вероятностного пространства: (W,E,Р) или (W,F,Р). Вероятностное пространство определяет вероятностную модель рассматриваемого случайного явления.

Свойства вероятностей (следствия из аксиом)

1. Вероятность невозможного события равна нулю: Р(Æ)=0

Доказательство: Так как невозможное событие Æ несовместно с любым другим событием А, АÆ=Æ, то из аксиомы 3 следует, что Р(АÈÆ)=Р(А)+Р(Æ). С другой стороны, так как АÈÆ=А (добавление невозможного события не изменяет события А), то Р(АÈÆ)=Р(А). Следовательно, Р(Æ)=0.ð

2. Р()=1-Р(А)

Доказательство: Из А+=W, А=Æ и аксиом 2,3 следует:

P(A)+P()=P(W), P()=1-P(A) —

3. Если АÌВ, то Р(А)£Р(В)

Доказательство: Разложим В на два несовместных события: В=А+. Получим в силу аксиомы 3: Р(В)=Р(А)+Р(), откуда следует, что Р(В)³Р(А).ž

Таким образом, если событие А может произойти только вместе с событием В, то вероятность события А не может быть больше вероятности события В.

4. Р(А)£1 для любого А.

Доказательство: Из того, что любое событие А может произойти только с достоверным событием: А=АWÌW, а также из свойства 3 и аксиомы 2 следует Р(А)£Р(W)=1.˜

5. Теорема сложения вероятностей. Для любых А и В справедливо

Р(АÈВ)=Р(А)+Р(В)-Р(АВ)

Доказательство: AÈB=A+B,

P(AÈB)=P(A)+P(B) (1)

C другой стороны, любое событие можно разложить на два несовместных события:

B=AB+B,

P(B)=P(AB)+P(B), откуда

P(B)=P(B)-P(AB).

Подставляя это выражение для Р(В) в (1) получаем:

Р(АÈВ)=Р(А)+Р(В)-Р(АВ) —

6. Теорема сложения вероятностей для n событий:

Доказательство: Методом математической индукции. При n=2 теорема доказана. Пусть она верна для (n-1) события; покажем, что при этом она верна для n событий. Обозначим В=, тогда

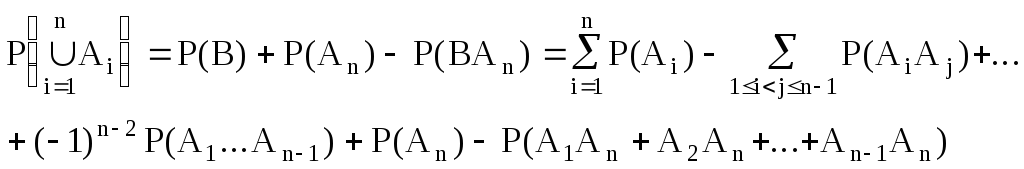(2)

В свою очередь для (n-1) событий вида имеем:

(3)

Подставляем (3) в (2) и получаем утверждение теоремы. †

7. Если ВÌА, то Р(А-В)=Р(А)-Р(В)

Доказательство:

А=В+(А-В);

Р(А)=Р(В)+Р(А-В); а это влечет:

Р(А-В)=Р(А)-Р(В). ƒ

8. Аксиома непрерывности.

Функция множеств Р(А) - непрерывна. Если А_n есть монотонно возрастающая последовательность множеств: A₁ÌA₂ÌA₃...ÌA_nÌ... и , , тогда

Доказательство: Согласно определению:

Если А₀=Æ

—

Определение вероятности, как меры измеримого пространства событий, позволяет по заданным (или определенным из эксперимента) вероятностям одних событий находить вероятности других более сложных событий, используя действия над событиями и свойства вероятности. Однако, данное определение не задает конкретную величину вероятности событий. Её можно определить теоретически лишь в некоторых частных случаях, и в общем случае - оценить экспериментально. Рассмотрим частные случаи, в которых вероятности событий можно рассчитать теоретически.