Теория Информации - Методичка (1 семестр)

Код называют совершенным, если для него сферы некоторого одинакового радиуса вокруг кодовых слов, не пересекаясь, покрывают все пространство.

Квазисовершенный код – это код, у которого сферы радиусом t вокруг каждого кодового слова не пересекаются и все слова, не лежащие внутри сфер, лежат на расстоянии t+1 хотя бы от одного кодового слова.

Основными параметрами блочного кода задаваемого отображением (4.1) являются: размерность кода k (т.е. длина информационных слов), длина кода n (длина кодовых слов) и минимальное кодовое расстояние dmin. Код с указанными параметрами кратко

называют: (n,k)-код или (n,k,dmin)-код. Отношение n/k называют из-

быточностью, а отношение k/n – скоростью кода.

4.3. Базовые оценки

Как узнать существует ли линейный (n,k)-код С, исправляющий t ошибок? В теории информации известен ряд оценок существования кода.

Рассмотрим здесь и далее блочный линейный помехоустойчивый (n,k)-код, заданный над конечным полем Fq, q=pm, где p – простое число. В этом случае Fqn можно рассматривать как n-мерное пространство над полем Fq. Наиболее частым является случай, когда q = 2.

Найти пределы возможных значений параметров произвольного линейного блокового кода можно с использованием границы Хемминга, называемую также границей сферической упаковки. Коды,

достигающие границы Хэмминга, называют совершенными или

плотноупакованными:

Значение в левой части неравенства оценивает число исправляемых комбинаций ошибок.

79

Оценка Варшамова–Гилберта. Линейный код над полем Fq

длиной n, размерностью k и минимальным кодовым расстоянием d существует, если параметры n, d, k удовлетворяют условию:

Если произвольным образом выбрать параметры кода и эти значения будут удовлетворять оценке Варшамова–Гилберта, то линейный код с такими параметрами существует. Если для выбранных параметров не выполняется граница Хемминга, то кода с такими параметрами не существует. А если для выбранных значений оценка Варшамова-Гилберта не выполняется, а граница Хемминга выполняется? Для параметров из указанного диапазона есть ряд частных результатов, однако в целом ответа на этот вопрос нет.

Оценка Синглтона. Для линейного (n, k, d)-кода, заданного над полем 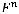имеет место оценка

Коды, для которых достигается оценка Синглтона, называются кодами с максимальным расстоянием (или MDR-кодами).

Оценка Грайсмера применима к двоичным кодам. Обозначим через N(k,d) минимальную длину линейного двоичного кода размерностью k и минимальным расстоянием d:

Краткие итоги

Основная идея помехоустойчивого кодирования состоит во внесении в данные специальным образом организованной избыточности.

Существует большое количество параметров, по которым классифицируют помехоустойчивые коды.

Известные оценки не всегда могут дать однозначный ответ о существовании линейного блочного кода с заданными параметрами.

80

Рекомендуемая литература

1.Сидельников В.М. Теория кодирования / В.М. Сидельников. – М.: Физматлит, 2008. – 324 с.

2.Ромащенко А.Е. Заметки по теории кодирования / А.Е. Ромащенко, А.Ю. Румянцев, А. Шень. – М.: МЦНМО, 2011. – 80 с.

3.Морелос-Сарагоса Р. Искусство помехоустойчивого кодирования. Методы, алгоритмы, применение / Р. Морелос-Сарагоса. – М.: Техносфера, 2005. – 320 с.

4.Блейхут Р. Теория и практика кодов, контролирующих ошибки / Р. Блейхут. – М.: Мир, 1986. – 576 с.

5.Мак-Вильямс Ф. Дж. Теория кодов, исправляющих ошибки

/Ф. Дж. Мак-Вильямс, Н. Дж. А. Слоэн.– М.: Связь, 1979. – 744 с.

Набор для практики по теме «Введение в теорию помехоустойчивого кодирования»

Проверьте уровень освоения материала по теме «Введение в теорию помехоустойчивого кодирования», используя предложенные тесты.

Индивидуальное задание

Изобразите границы Хемминга и Варшамова–Гилберта некоторого (n, k, d)-кода С на одном графике. Рекомендации: ограничьтесь ситуацией q=2 и воспользуйтесь формулами приближенного вычисления биномиальных коэффициентов. В качестве осей графика можно выбрать значения k/n и d/n. Графики можно построить для конкретного значения t или для t, вычисленного как доля от одного из параметров кода.

81

Упражнения

Проверьте, возможно ли существование (n,k,d)-кода, заданного над полем Fq с указанными в задании параметрами. Выполняются ли для этого кода известные Вам оценки. Сделайте вывод по результатам вычисления.

82

Тесты

Вариант 1

1. Двоичный блочный код задан множеством своих кодовых слов: {00001, 10101, 10010, 10001}. Чему равно минимальное кодовое расстояние этого кода?

а) 1; б) 2; в) 2; г) 3.

2. Дан двоичный (n,k,d)-код. Сколько кодовых слов в этом

коде?

а) n2; б) 2n; в) 2k; г) n.

3. Код, рассмотренный в примере 4.1, является:

Вариант 2

1. Двоичный блочный код задан множеством своих кодовых слов: {00000, 10111, 10110, 10010}. Чему равно минимальное кодо-

2. Дан двоичный (7,4,3)-код. Сколько кодовых слов в этом

коде?

а) 72; б) 27; в) 24; г) 7.

83

3. Код, рассмотренный в примере 4.1, является:

4. Один и тот же код одновременно может быть:

Вариант 3

1. Двоичный блочный код задан множеством своих кодовых слов: {0000, 1111, 1110, 0010}. Чему равно минимальное кодовое

84

5. МАТРИЧНОЕ ОПИСАНИЕ ЛИНЕЙНЫХ БЛОЧНЫХ КОДОВ

Эта глава посвящена изучению матричного подхода к описанию линейных блочных кодов. Изложен способ построения универсальных кодера и декодера для любого блочного линейного кода, а также рассмотрены специальные кодер и декодер двоичных кодов Хемминга.

Ключевые слова: порождающая и проверочная матрицы; связь проверочной и порождающей матриц; дуальный код; вес Хемминга; лемма о минимальном кодовом расстоянии; теорема о кодовом слове веса w; теорема о минимальном весе кода; теорема о систематическом виде порождающей матрицы; понятие эквивалентных порождающих матриц; эквивалентные коды; синдром; смежный класс; лидер смежного класса; лидерное декодирование; самодуальные коды; код Хемминга.

В гл. 4 дано определение коду, как отображению из пространства Xk в пространство Xn. Очевидно, что для построения такого отображения достаточно просто векторам одного пространства поставить в соответствие векторы другого пространства. Например:

Но наиболее естественным способом построения соответствия между информационными и кодовыми словами является применение некоторой линейной операции: с=F(i). В качестве функции F часто выбирают умножение на матрицу. Рассмотрим такой способ построения кодов подробнее.

85

5.1. Порождающая и проверочная матрицы

Итак, любой линейный код С образует подпространство в Fqn. Любое множество базисных векторов в этом подпространстве может быть использовано для построения (n k)-матрицы G, которая называется порождающей матрицей кода. Тогда любое кодовое слово из C может быть представлено как линейная комбинация строк из G. Множество из qk кодовых слов (каждое из них длиной n) называется (n,k)-кодом. Любой вектор из С можно представить в виде:

где с – кодовое слово; i – информационное слово; G – порождающая матрица кода C.

Если воспользоваться известными из алгебры сведениями о количестве невырожденных матриц, которые можно построить над конечным полем

Fq, то можно показать, что линейный код имеет

(qk–1)(qk–q)(qk–q2)…(qk–qk-1)

различных порождающих матриц.

Так как код С – это подпространство, то для него можно построить ортогональное дополнение С , которое также будет являться подпространством и само может рассматриваться как код.

Код С , образованный всеми векторами, которые являются ортогональными ко всем векторам кода С, называется дуальным (или двойственным) к коду С.

Теорема о дуальном коде. Код Сявляется линейным кодом над полем Fq и имеет размерность n–k, где k=dim С.

Порождающая матрица дуального кода С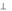является прове-

рочной матрицей кода С.

Очевидно, что для заданного кода С, его порождающая матрица G и проверочная матрица H связаны равенством:

GHт=0. (5.2)

Это равенство легко доказать, используя факт о том, что строки этих матриц есть базисы двух ортогональных пространств.

86

Пример 5.1. Рассмотрим (5,3) код С, заданный над полем F2. Пусть для него заданы порождающая и проверочная матрицы:

Очевидно, что для заданных матриц выполняется равенство (5.2). Построим множество всех кодовых векторов кода С [используем формулу (5.1)].

В гл. 4 мы обсуждали, как оценить число исправляемых кодом ошибок, используя минимальное кодовое расстояние dmin, и даже рассмотрели способ его вычисления. Однако существует более простой способ вычисления dmin.

Функция wt(а), равная числу отличных от нуля координат вектора а, называется весом Хемминга вектора а, или просто весом вектора.

Лемма о вычислении минимального кодового расстояния

Минимальное кодовое расстояние dmin кода С, заданного над Fq, равно минимальному весу ненулевого кодового слова кода С:

dmin=min{wt(a)| a C, a 0}.

Доказательство. Очевидно, что

d(a1,a2)=d(a1+a2,0)= wt(a1+a2).

87

Из свойств линейности кода имеем, что a1+a2 С. Отсюда следует, что минимальное расстояние может быть вычислено как минимальный вес по всем qk–1 ненулевым кодовым словам.

Задача вычисления dmin через веса кодовых слов значительно легче, чем задача вычисления их через перебор по всем парам кодовых слов.

Минимальное кодовое расстояние это очень важный параметр кода. Чем больше dmin, тем больше ошибок код может обнаружить и исправить. Двоичный линейный (n,k)-код С с минимальным расстоянием Хемминга dmin 2t+1 может обнаружить dmin–1 ошибок и исправить t ошибок.

5.2. Теоремы о проверочной и порождающей матрицах кода С

Пусть дан линейный блочный (n,k,dmin)-код С, заданный над полем Fq и определенный матрицами G и H. Рассмотрим несколько

теорем, необходимых для дальнейшего изложения материала.

Теорема о кодовом слове веса w. Код С содержит ненулевое кодовое слово веса Хемминга не более w тогда и только тогда, когда Н содержит множество из w линейно зависимых столбцов.

Доказательство.

Для любого кодового слова с выполняется равенство сHт=0. Пусть wt(c)=w. Исключим из рассмотрения нулевые компоненты вектора с. Полученное равенство будет соотношением линейной зависимости w столбцов из Н. Следовательно, Н содержит множество из w линейно зависимых столбцов.

И наоборот, если Н содержит множество из w линейно зависимых столбцов, то найдется равная нулю линейная комбинация, составленная не более чем из w столбцов. Соответствующие w ненулевых коэффициентов определяют вектор веса не более w, для кото-

рого сHт=0.

88