
Теория Информации - Методичка (1 семестр)
.pdf
Теорема о минимальном весе кода. Код С имеет минималь-
ный вес w тогда и только тогда, когда каждое множество из w–1 столбцов матрицы Н линейно независимы. 
Из этой теоремы следует: чтобы найти (n,k)-код с минимальным расстоянием d, достаточно найти (n-k) n-матрицу Н, в которой d любых столбцов независимы.
Из данного (n,k)-кода можно получить новый код, если выбрать две позиции в кодовом слове и переставить в каждом кодовом слове символы на этих позициях. Этот новый код будет отличаться от исходного только видом кодовых слов, а все параметры кода сохранятся. Говорят, что такой код эквивалентен исходному.
Порождающие матрицы G1 и G2 эквивалентных кодов могут быть получены друг из друга с помощью элементарных операций над строками и перестановкой столбцов. Каждая порождающая матрица G эквивалентна некоторой матрице канонического ступенчатого вида. Легко показать, что если порождающие матрицы содержат линейно независимые векторы, то и в матрице канонического вида все строки будут ненулевыми.
Эквивалентную матрицу можно записать в виде:
(5.3)
где 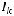 – единичная подматрица с размера-
– единичная подматрица с размера-
ми k k; 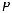 – проверочная подматрица с размерами k (n–k).
– проверочная подматрица с размерами k (n–k).
Если порождающая матрица представлена в виде (5.3), то ее называют порождающей матрицей в систематическом виде. Естественно определить проверочную матрицу в систематическом виде:
|
|
|
H |
Pò I |
n |
k |
, |
(5.4) |
|
|
|
|
|
|
|
||
где |
|
|
– транспонированная подматрица из выражения (5.3), |
|||||
|
|
|
– единичная подматрица с размерами (n–k) |
(n–k). |
||||
|
Очевидно, что если код задан с помощью матриц в система- |
|||||||
тическом виде, то и сам код будет систематическим. |
|
|||||||
89
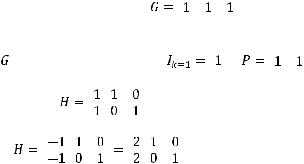
Пример 5.2. По заданной матрице |
|
кода С по- |
строить проверочную матрицу, считая, что код С а) задан над F2, |
||
б) задан над F3. |
|
|
Матрицу составляют подматрицы |
и |
. |
Тогда для двоичного случая: |
|
|
,
для случая F3:
.
Теорема о систематическом виде порождающей матрицы.
Каждый линейный код эквивалентен систематическому линейному коду.
5.3. Синдромы и смежные классы
Умножение верного кодового слова с на транспонированную проверочную матрицу дает в результате ноль:
сHт=0.
Что произойдет, если заменить верное кодовое слово с на слово, со-
держащее ошибку v=c+e, где e – вектор ошибки: s=vHт=(c+e)Hт=eHт.
Результирующий вектор s=eHт будет содержать в закодированном виде информацию об ошибках, которые повредили верное кодовое слово. Этот вектор принято называть синдромом по аналогии с медицинским термином, который позволяет определить болезнь пациента. Синдром в теории информации позволяет найти ошибку (болезнь) вектора, полученного из канала связи.
Если синдром равен нулю, то можно сделать вывод, что из канала получено верное кодовое слово, или это слово было так повреждено в канале, что превратилось в другое верное кодовое слово. В таких ситуациях декодер принимает решение о том, что получено верное кодовое слово. Если же синдром не равен нулю, то необхо-
90

димо по искаженному кодовому слову попытаться найти верное кодовое слово.
Будем говорить, что все кодовые слова сi C, поврежденные одним и тем же вектором ошибок, лежат в одном смежном классе.
Теорема о смежных классах. Все векторы из одного смежного класса имеют одинаковый синдром, присущий только этому смежному классу.
Доказательство.
Если векторы v1 и v2 (v1 v2) лежат в одном смежном классе, то для них справедливо v1=сi+e, v2=cj+e для некоторого вектора ошибок e и кодовых слов сi, сj. Для каждого кодового слова выполняется сHт=0, отсюда: s1=v1Hт= eHт, s2=v2Hт= eHт, следовательно s1=s2.
Обратное, если s1=s2, тогда (v1–v2)Hт=0, следовательно, разность (v1–v2) является кодовым словом и значит, что v1 и v2 принадлежат одному смежному классу.
Вектор минимального веса в смежном классе называют ли-
дером класса.
Пример 5.3. Рассмотрим код из примера 5.1. Для вектора ошибок, е=10000, построим смежный класс. Для этого все кодовые векторы
{00000, 00111, 01001, 01110, 10010, 10101, 11011, 11100}
просуммируем с вектором ошибок по модулю 2:
{10000, 10111, 11001, 11110, 00010, 00101, 01011, 01100}.
Легко проверить, что всем искаженным векторам соответствует один и тот же синдром s=10. Таким образом, мы построили смежный класс. Лидером этого класса будет вектор минимального веса: 10000, wt(10000)=1. Обратите внимание, что лидером класса является вектор ошибок.
Сколько же существует различных смежных классов? Ровно столько же сколько существует различных синдромов. А сколько существует синдромов? Можно посчитать. Синдром получают в результате умножения вектора на матрицу s=vHт. Исходя из размерно-
91
сти используемых величин видно, что синдром – это вектор длиной n–k. Следовательно, общее число синдромов и общее число смежных классов qn–k, где q – мощность кодового алфавита.
Итак, для кодов, заданных в матричном виде, мы можем кодировать информационные слова, умножая их на порождающую матрицу, умеем с помощью проверочной матрицы определять, является ли вектор, принятый из канала связи, верным кодовым словом. Что нужно делать дальше, чтобы декодировать всю принятую последовательность? Существуют два подхода к построению декодера. Первый – построение универсального декодера, который подходит для работы с произвольными кодами рассматриваемого класса кодов. Второй – построение специального декодера, который учитывает особенности кода и декодирует его либо быстрее универсального, либо с меньшими техническими затратами. Рассмотрим алгоритм работы универсального лидерного декодера блочных линейных кодов.
5.4. Лидерное декодирование
Рассмотрим (n,k)-код, заданный над полем F2 и определенный матрицами G и H. Создадим таблицы, необходимые для работы декодера (табл. 5.1 и 5.2).
Табл. 5.1 кодовых слов состоит из двух столбцов и 2k строк. В первом столбце запишем все информационные слова кода, а во втором – кодовые слова, соответствующие информационным словам. Для получения кодовых слов используем формулу c=iG.
Табл. 5.2 синдромов и лидеров классов содержит 2n–k строк и два столбца. В первом столбце запишем все возможные синдромы, а во втором – соответствующие им лидеры смежных классов, или (что то же самое) векторы ошибок, вызывающие появление соответствующего синдрома.
92
|
Таблица 5.1 |
Кодовые слова |
|
|
|
i F2k (информаци- |
c F2n, (кодовые |
онные слова) |
слова) |
|
|
i1 |
c1 |
i2 |
c2 |
… |
… |
|
|
i2k |
c2k |
|
|
Таблица 5.2 Синдромы и лидеры классов
s=vHт |
V (векторы |
(синдромы) |
ошибок) |
|
|
s1 |
v1 |
s2 |
v2 |
… |
… |
|
|
s2n k |
v2n k |
|
|
Алгоритм декодирования полученного из канала слова v представлен на рис. 5.1.
Шаг 1
Шаг 2
Шаг 3
•Вычислить синдром s=vHт
•Если s=0, то с=v и переход на шаг 3.
•Если s 0, то найти этот синдром в столбце синдромов таблицы синдромов и лидеров классов.
•Просуммировать полученный из канала вектор v и вектор ошибок e, соответствующий синдрому (из таблицы синдромов) с=v+e.
•Считаем слово c верным кодовым словом, находим его во втором столбце таблицы кодовых слов. Соответствующее ему информационное слово (из первого столбца этой таблицы) и будет результатом декодирования.
Рис. 5.1. Алгоритм декодирования кодового слова
Рассмотрим примеры помехоустойчивого кодирования и декодирования с помощью матричного описания кодов.
Пример 5.4. Код С над полем F2 задан порождающей матри-
цей:
93
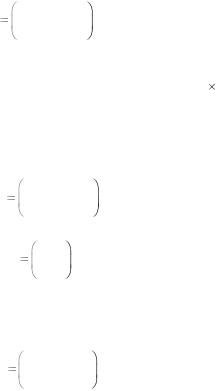
G |
1 |
1 |
1 |
0 . |
|
0 |
0 |
1 |
1 |
Определить основные параметры эквивалентного систематического кода и декодировать слово 0101.
Известно, что генерирующая матрица имеет размер k n, где k – число строк матрицы, а n – число столбцов. Скорость кода вычисляется как отношение k/n. Следовательно, в задании рассматривается (4,2)-код, скорость которого равна 2/4=1/2.
Преобразуем матрицу G в систематический вид Gsys=(I|P), для чего переставим второй и четвертый столбцы:
Gsys |
1 |
0 |
1 |
1 . |
|
0 |
1 |
1 |
0 |
Таким образом, проверочная подматрица
Ð |
1 |
1 . |
|
1 |
0 |
Отметим, что в данном случае выполняется соотношение Р=Рт. Коды, у которых выполняется такое соотношение, называются самодуальными. Согласно формуле Нsys=(–Pт|I), запишем проверочную матрицу:
Í sys |
1 |
1 |
1 |
0 . |
|
1 |
0 |
0 |
1 |
Для построения декодера составим матрицы кодовых слов и матрицы синдромов. Информационными словами i являются все возможные двоичные слова длиной k=2. Кодовые слова c вычислим, используя формулу c=iG. Отметим, что в зависимости от того, в систематическом или несистематическом виде использовать порождающую матрицу, одному и тому же информационному слову могут соответствовать различные кодовые слова. Но так как для декодирования мы будем использовать матрицу Н в систематическом виде, то и матрицу G нужно использовать систематическую. Для используемых матриц должно выполняться равенство GHт=0. Построим таблицу кодовых слов.
Информационные слова |
Кодовые слова в систематической форме |
94
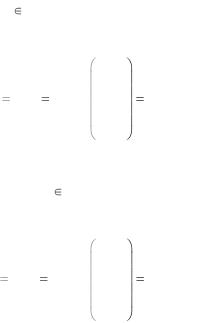
00 |
0000 |
01 |
0110 |
10 |
1011 |
11 |
1101 |
Построим таблицу синдромов и лидеров классов. Для этого организуем таблицу из двух столбцов и 2n–k=24–2=22=4 строк. Найдем произвольное слово e1 F2n минимального веса Хемминга, не являющееся кодовым и не включенное в предыдущие строки таблицы. Пусть e1=1000, вычисляем синдром этого вектора по формуле:
|
1 |
1 |
|
s eH ò (1000) |
1 |
0 |
(11) . |
|
1 |
0 |
|
|
0 |
1 |
|
Запишем полученный синдром s1=11 в первый столбец таблицы, а во второй столбец запишем вектор e1=1000. Далее находим новое произвольное слово e2 F2 минимального веса Хемминга, не являющееся кодовым и не включенное в предыдущие строки таблицы синдромов. Пусть e2=0100, вычисляем синдром этого вектора:
|
1 |
1 |
|
s eH ò (0100) |
1 |
0 |
(10) . |
|
1 |
0 |
|
|
0 |
1 |
|
Запишем полученный синдром s2=10 и соответствующий ему вектор ошибок во вторую строку таблицы синдромов. Продолжим аналогично до полного заполнения всех 2n–k строк таблицы
Синдромы s |
Лидеры классов (векторы ошибок) e |
|
|
00 |
0000 |
|
|
11 |
1000 |
|
|
10 |
0100 |
|
|
01 |
0001 |
|
|
95
Итак, у рассматриваемого кода 4 смежных класса, лидерами которых являются: e0=0000, e1=1000, e2=0100, e3=0001.
При построении таблицы в качестве вектора ошибок не был выбран вектор e=0010. Причина этого в том, что синдром вектора е=0100 совпадает с синдромом вектора e2=0100, что, в свою очередь, происходит из-за того, что данный код является кодом с неравной защитой от ошибок, т. е. число исправляемых ошибок зависит от местоположения ошибок. Из таблицы видно, что есть векторы ошибок весом 1, которые данный код не может исправить. Заранее оценить корректирующую способность кода, можно используя значение минимального кодового расстояния.
Согласно заданию, из канала получено v=0101. Если сравнить его со списком кодовых слов, то видно, что в смысле расстояния Хемминга, полученное слово ближе всего к кодовому слову 1101, т. е. можно предположить, что информационным словом, соответствующим полученному из канала v=0101, будет i=11. Проверим это предположение по алгоритму декодирования.
Вычислим синдром s=11. В таблице синдромов этому синдрому соответствует вектор ошибок e=1000. Суммируем вектор ошибок и вектор, полученный из канала связи: v+e=0101+1000=1101. Находим вектор 1101 в таблице кодовых слов (вектор находится в последней строке таблицы). Соответствующий информационный вектор i=11 и является результатом декодирования.
Оценим теперь корректирующие способности этого кода. Для чего вычислим минимальное расстояние Хемминга для данного кода, как минимум хемминговых весов ненулевых кодовых слов кода С. Веса Хемминга кодовых слов: wth(0110)=2, wth(1011)=3, wth(1101)=2. Минимальное расстояние Хемминга: dmin=min{2, 3, 2}=2 и означает, что рассматриваемый код гарантированно обнаруживает 1 ошибку, а исправляет 0 ошибок.
Пример 5.5. Код С над F2 задан проверочной матрицей:
96
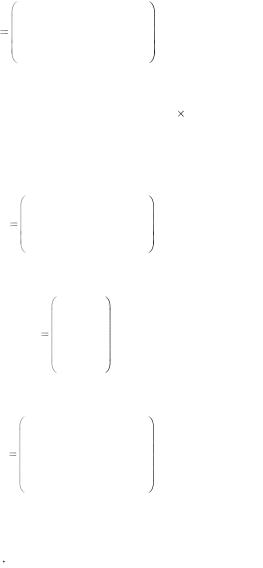
|
1 |
1 |
1 |
0 |
1 |
0 |
0 |
H |
0 |
1 |
1 |
1 |
0 |
1 |
0 . |
|
0 |
0 |
1 |
1 |
1 |
0 |
1 |
Определить основные параметры эквивалентного систематического кода и декодировать слова 001011 и 0111111.
Проверочная матрица Н имеет размер (n–k) n. Следовательно, длина кода n=7, размерность кода k=n–(n–k)=7–3=4, скорость кода равна 4/7.
Приведем матрицу H к систематическому виду. Переставим местами столбцы 2 и 6, 3 и 7.
|
|
1 |
0 |
0 |
0 |
1 |
1 |
1 |
H |
sys |
0 |
1 |
0 |
1 |
0 |
1 |
1 . |
|
|
|
|
|
|
|
|
|
|
|
0 |
0 |
1 |
1 |
1 |
0 |
1 |
Правые четыре столбца матрицы Hsys представляют собой транспонированную проверочную подматрицу Р:
|
0 |
1 |
1 |
Ð |
1 |
0 |
1 . |
|
1 |
1 |
0 |
|
1 |
1 |
1 |
Согласно формуле Gsys=(Ik|P), запишем порождающую матрицу в систематическом виде:
|
1 |
0 |
0 |
0 |
0 |
1 |
1 |
|
Gsys |
0 |
1 |
0 |
0 |
1 |
0 |
1 . |
|
0 |
0 |
1 |
0 |
1 |
1 |
0 |
||
|
||||||||
|
0 |
0 |
0 |
1 |
1 |
1 |
1 |
Построим таблицу кодовых слов. Число кодовых слов определяется как 2k=24=16. Информационными словами i являются все возможные двоичные слова длиной k=4. Кодовые слова c вычислим, используя формулу c=i G и используя матрицу Gsys.
i i |
ci |
i i |
ci |
i i |
ci |
0000 |
0000000 |
0110 |
0110011 |
1100 |
1100110 |
97

0001 |
0001111 |
0111 |
0111100 |
1101 |
1101001 |
0010 |
0010110 |
1000 |
1000011 |
1110 |
1110000 |
0011 |
0011001 |
1001 |
1001100 |
1111 |
1111111 |
0100 |
0100101 |
1010 |
1010101 |
– |
– |
0101 |
0101010 |
1011 |
1011010 |
– |
– |
Построим таблицу синдромов. Используем число различных синдромов этого кода 2n–k=27–4=8. У рассматриваемого кода 8 смежных классов, лидерами которых являются: e0=0000000, e1=0000001, e2=0000010, e3=0000100, e4=0001000, e5=0010000, e6=0100000, e7=1000000.
Синдромы s |
Лидеры классов |
|
(векторы ошибок) e |
|
|
000 |
0000000 |
|
|
111 |
0000001 |
|
|
110 |
0000010 |
|
|
101 |
0000100 |
|
|
011 |
0001000 |
|
|
001 |
0010000 |
|
|
010 |
0100000 |
|
|
100 |
1000000 |
Декодируем слово 001011. Вычислим синдром s=0. Нулевой синдром говорит о том, что кодовое слово не содержит ошибок. Найдем его в таблице кодовых слов. Результатом декодирования будет соответствующее ему информационное слово 0010.
Декодируем слово 0111111. Вычислим синдром s = 100. Этому синдрому соответствует вектор ошибок 1000000. Следовательно, верное кодовое слово с=0111111+1000000=1111111. Вектору с соответствует информационное слово 1111.
Оценим корректирующие способности этого кода. Минимальное расстояние Хемминга этого кода найдем как минимум хем-
минговых весов dmin=min{wth(0001111)=4, wth(0010110)=3, wth(0011001)=3, wth(0100101)=3, wth(0101010)=3, wth(0110011)=4, wth(0111100)=4, wth(1000011)=3, wth(1001100)=3, wth(1010101)=4,
98
