Теория Информации - Методичка (1 семестр)

6.О МОДИФИКАЦИИ КОДОВ, ДЕКОДЕРОВ

ИНОВЫХ ОБЛАСТЯХ ПРИМЕНЕНИЯ КОДОВ

Вэтой главе рассмотрены возможности модификации параметров известных кодов в целях получения кодов с заданными параметрами; возможности модификации декодеров с целью получить коды с большими возможностями по исправлению ошибок, чем гарантируется минимальным кодовым расстоянием, а также возможности использования помехоустойчивых кодов в задачах защиты данных не от помех, а от несанкционированного доступа к ним.

Ключевые слова: модификация кодов, комбинирование кодов, укорочение, расширение, перфорация, пополнение, удлинение кодов; модификация кодов выбрасыванием кодовых слов; универсальные и специальные декодеры; списочные, детерминированные, вероятностные, мягкие, жесткие декодеры; критерии сравнения декодеров; помехоустойчивые коды в криптографии; криптосистема Мак-Элиса; криптосистема Нидеррайтера.

В предыдущих главах объяснено как определять, существует ли код с заданными характеристиками и как узнавать корректирующие способности конкретного кода. Кроме этого, показано, что в реальных системах помехоустойчивой защиты не используются универсальные декодеры, а строятся декодеры, основанные на алгебраической специфике конкретных кодов, что позволяет декодировать быстро и с минимальными техническими затратами.

Теперь изучим, как можно модифицировать известный код, с хорошими корректирующими способностями в случае, когда он не подходит для конкретного практического приложения по таким параметрам, как длина кода, размерность или минимальное кодовое расстояние.

Рассмотрим особые виды декодеров, а также несколько вариантов применения помехоустойчивого кодирования в задачах, отличных от исправления случайных ошибок в каналах связи.

108

6.1. Методы модификации помехоустойчивых блочных кодов

Новый код с требуемыми характеристиками можно получить на основе известного кода с помощью одного из методов модификации или комбинирования кодов. Обычно модификацией кода называют изменения, вносимые в один код, а в случае, когда новый код формируется из нескольких известных кодов, говорят о комбинировании кодов. Далее будем рассматривать только методы модификации кодов.

Для всех рассмотренных кодов длину и размерность нового модифицированного кода можно определить заранее, а априорное вычисление минимального кодового расстояния либо затруднительно, либо невозможно.

Обозначим через С линейный блочный (n, k, d)-код над полем Fq с порождающей матрицей G и проверочной матрицей H, где n – длина кода, k – размерность кода, d – минимальное кодовое расстояние.

Укорочение кода С заключается в уменьшении числа информационных символов кода. Пусть порождающая матрица G кода С задана в систематическом виде, тогда порождающая матрица Gs укороченного (n-s, k-s, ds)-кода Cs строится из G удалением s (0<s<k) столбцов единичной подматрицы Ik и s строк, соответствующих ненулевым элементам удаляемых столбцов. Связь минимальных расстояний исходного и модифицированного кода определяется не-

равенством: ds d.

Важное свойство укороченных циклических кодов Сs состоит в том, что для них могут быть использованы те же самые кодеры и декодеры, как и для исходных кодов, хотя укороченные коды и не сохраняют устойчивость к циклическому сдвигу. Для компьютерного моделирования гораздо проще дополнять слова нулями на старших позициях и использовать те же самые алгоритмы кодирования и декодирования.

109

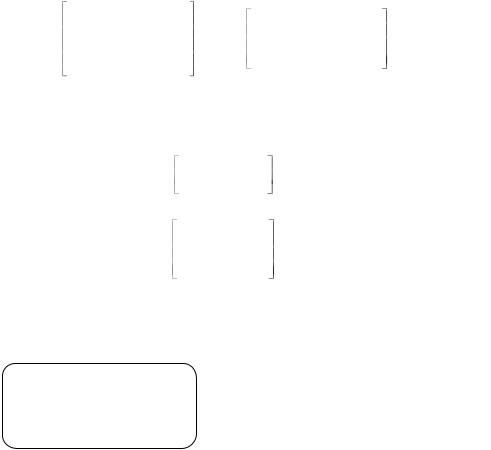
Пример 6.1. Рассмотрим (7,4,3)-код Хемминга. Этот код задан порождающими матрицами:

Для построения укороченного (5, 2, 3)-кода можно удалить любые два из четырех левых столбцов матрицы G. Удалим первую и вторую строки матрицы G. Оставшиеся элементы образуют порождающую матрицу:

а проверочная матрица укороченного кода имеет вид:

Из множества кодовых слов укороченного кода {00000, 10110, 01011, 11101} видно, что ds=3.

Используем алгоритм Хемминга для кодирования и декоди-

алгоритму Хемминга: b=(1,0,1,1,0). Предположим, что после передачи слова по каналу мы полу-

чили вектор v=(1,1,1,1,0).

Вычисляем синдром s=(0,1,1). Делаем вывод, что слово искажено ошибкой. По синдрому вычисляем (0,1,1)2=210 и делаем предположение, что неправильно принят второй бит.

Следовательно, b=(1,0,1,1,0) и результат декодирования 10.

110

Итак, полученный после укорочения (5, 2, 3)-код перестал быть циклическим, количество проверочных символов осталось таким же, а информационных символов на два меньше.

Расширение кода С состоит в добавлении 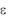проверочных символов. Расширенный (n+ , k, dext)-код Сext имеет минимальное расстояние dext d. Расширенная проверочная матрица Нext размером (n–k+ )×(n+ ) получается из проверочной матрицы исходного кода С добавлением столбцов и строк:

Расширение кода с помощью добавления проверки на четность можно выполнить следующим образом:

Известно, что в общем случае коды, расширенные проверкой на четность, обладают минимальным расстоянием dext на единицу превышающем минимальное расстояние исходного кода dmin, если значение dmin – нечетное, и dext совпадает с dmin в случае четного зна-

чения dmin.

Пример 6.2. Расширим (7,4,3)-код из примера 1 проверкой на четность:

111

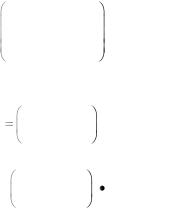
Тогда информационному слову 1010 будет соответствовать кодовое слово (0,1,1,1,0,1,0,0).

Предположим, что после передачи слова по каналу получен вектор v=(0,1,0,1,0,1,0,0). Синдром s=(1,1,1,1) показывает ошибку в третьем бите. Следовательно, верное кодовое слово – (0,1,1,1,0,1,0,0), а соответствующее ему информационное – 1010.

Полученный расширенный код имеет большую избыточность, чем (7, 4, 3)-код Хемминга и, следовательно, он может исправлять большее число комбинаций ошибок.

Перфорация линейных блочных кодов состоит в удалении проверочных символов, что приводит к блочному (n–р, k, dр)-коду Ср с минимальным расстоянием dp<d. Для проведения перфорации используется матрица Н в систематическом виде. Проверочная матрица Нр перфорированного кода Ср получается удалением р столбцов единичной подматрицы In–k матрицы H и р строк матрицы Н исходного кода, соответствующих ненулевым элементам удаляемых столбцов.

Помехоустойчивый код, к которому применили перфорирование, называется перфорированным или выколотым кодом.

Пример 6.3. Рассмотрим (5,2,3)-код, заданный проверочной матрицей:

0 1 1 0 0 H = 1 1 0 1 0 .

1 0 0 0 1

Удаление третьего столбца и верхней строки дает проверочную матрицу Hр перфорированного (4, 2, 2)-кода Cр,

порождающая матрица этого кода имеет вид:

112

Пополнение кода состоит в добавлении новых кодовых слов к исходному коду. Простым способом выполнения этой модификации при сохранении линейности кода является добавление линейно независимых строк в порождающую матрицу. Построенный

таким образом код Cadd имеет параметры (n, k+δ, dadd), где δ – число добавленных строк. Минимальное расстояние Cadd есть dadd < d. По-

рождающая матрица пополненного кода выглядит следующим образом:

G

где pi – это векторы длиной n, которыми пополняют код С. Общеизвестным способом пополнения линейного блокового

(n, k, d)-кода С является добавление кодового слова из всех единиц (если таковое уже не принадлежит коду).

Модификация кода выбрасыванием кодовых слов состоит в удалении некоторых кодовых слов из кода из всего множества кодовых слов. В общем случае это приводит к нелинейному коду. Способ, сохраняющий линейность, состоит в удалении строк порождающей матрицы G исходного кода. В результате получается код Сехр с параметрами (n, k–l, dехр), dехр ≥ d. Для систематического кода операции выбрасывания и укорочения совпадают.

Операция удлинения кода выполняется добавлением j столбцов и j строк к порождающей матрице, т.е. добавляются j проверочных и j информационных символов. Обычный способ удлинения состоит из последовательного выполнения двух операций: пополнения кода путем добавления единичного вектора и расширения его с помощью общей проверки на четность. В результате этих операций число информационных символов увеличивается на единицу.

113

6.2. Классификация декодеров линейных кодов

Рассмотрим классификацию декодеров, опираясь на понятия, использованные в литературе, связанной с помехоустойчивым кодированием.

Декодеры по логике работы можно разделить на ряд групп. В зависимости от возможности их применения к различным кодам декодеры делят на специальные и универсальные. Специальные декодеры позволяют декодировать кодовые слова только определенных кодов, а в некоторых случаях только кодов с параметрами из определенного диапазона значений. Универсальные декодеры позволяют декодировать произвольные коды из определенного класса, например, как было рассмотрено, лидерный декодер подходит для всех блочных линейных кодов.

Рассмотренные примеры декодеров всегда выдавали на выходе точно одно информационное слово. Однако так действуют не все декодеры. По количеству кодовых слов, получаемых на выходе декодера, разделяют списочные и не списочные декодеры. Списочные декодеры возвращают список наиболее вероятных слов, при этом длина списка определяется параметрами алгоритма. Верное кодовое слово может и не содержаться в списке, возвращаемом декодером. Обычно это возникает при большом числе ошибок в канале связи. Несписочные декодеры всегда возвращают одно кодовое слово.

По числу исправляемых ошибок разделяют детерминированные и вероятностные декодеры. Детерминированные декодеры всегда правильно восстанавливают кодовое слово, если число ошибок не превосходит количество гарантированно исправляемых ошибок кода t. Если число ошибок даже незначительно превышает t, то вероятность верного декодирования резко стремится к нулю. Вероятностные декодеры всегда правильно восстанавливают кодовое слово, если число ошибок не превосходит t. Если число ошибок превышает количество гарантированно исправляемых ошибок кода t, то

114

декодер продолжает работать с высокой эффективностью, но правильность декодирования не является стопроцентной.

По взаимосвязи с демодулятором, разделяют декодеры с мягкими решениями и декодеры с жесткими решениями. Мягкие декодеры (декодеры мягких решений) объединяются с демодулятором и оперируют входными вещественными данными. Жесткие декодеры (декодеры жестких решений) оперируют целыми входными данными, заданными над некоторым фиксированным полем.

Один и тот же декодер может входить в несколько групп. Например, для кодов Рида–Маллера известны списочный декодер мягких решений, вероятностный, мягкий декодер и списочный декодер жестких решений.

В силу того, что для декодирования одних и тех же кодов применяются различные специальные декодеры, а также декодеры универсального типа, то необходимы критерии сравнения декодеров. Такими критериями могут быть количество ошибок, гарантированно исправляемых декодером в пределах одного кодового слова; вероятность правильного восстановления кодового слова при числе ошибок, превышающем число t; время работы декодера при фиксированных параметрах; объем памяти требуемой для работы; а также зависимость вероятности правильного декодирования от типа накладываемых ошибок.

6.3.Применение кодов, корректирующих ошибки,

взадачах криптографической защиты информации

Область применения помехоустойчивого кодирования не

ограничивается только исправлением ошибок. Существует ряд криптографических задач, для решения которых используют помехоустойчивые коды. Например, существуют системы по защите легально тиражируемой цифровой продукции от несанкционированного копирования, в основе которых лежат известные помехоустойчивые коды Рида–Соломона. Известны интересные решения реализации протоколов открытого распределения ключей с использованием

115

помехоустойчивых кодов с высокой плотностью проверок. Рассмотрим подробнее два варианта построения шифросистем на основе помехоустойчивых кодов.

Начнем рассмотрение с классического варианта широко известной асимметричной шифросистемы Мак-Элиса (McEliece R.J.). Пусть С – линейный (n,k,d)-код с порождающей матрицей G над полем Fq, гарантированно исправляющий t ошибок. Назовем этот код базовым кодом шифросистемы. Секретным ключом в этой шифросистеме являются случайная невырожденная матрица S с размерами k k и перестановочная матрица P с размерами n n. В качестве открытого ключа выступает произведение матриц E=SGP.

Рассмотрим протокол взаимодействия двух абонентов. Абонент Х хочет получить от абонента Y зашифрованное сообщение. Для этого X создает открытый и закрытый ключи и передает свой открытый ключ абоненту Y по общедо-

ступному каналу, т.е. в открытом виде. В системе Мак-Элиса зашифрованная информация, которую абонент Y передает абоненту X, представляет собой вектор:

b=aE+e,

где а – вектор длины k, содержащий секретную информацию; е – секретный вектор ошибок, который случайно и равновероятно выбирается абонентом Y среди всех векторов веса не выше t; E – открытый ключ.

Абонент Х, получив вектор b, строит вектор b =bP–1, который отличается от кодового вектора не более чем в t разрядах. Затем с помощью любого алгоритма декодирования кода С абонент X находит вектор а , который удовлетворяет условию: b =а G+e при этом wt(e ) t. Секретная информация, посланная абонентом Y восстанавливается в виде а= а S–1.

116

Близкой к шифросистеме Мак-Элиса является шифросистема Нидеррайтера (Niederreiter H.), особенность которой заключается в том, что конфиденциальная информация передается в искусственных векторах ошибок.

Пусть С – линейный (n,k,d)-код, гарантированно исправляющий t ошибок, заданный порождающей матрицей G. Тогда секретным ключом в этой шифросистеме так же, как и в шифросистеме Мак-Элиса, являются случайная невырожденная матрица S с размерами k k и перестановочная матрица P с размерами n n. В качестве открытого ключа выступает матрица E=SGP, где G – кодирующая матрица кода С.

В системе Нидеррайтера зашифрованная информация, которую абонент Y передает абоненту X, представляет собой вектор длины n–k вида s=eНт, где Н – некоторая проверочная матрица с размерами (n–k) n, такая, что EHт=0, е – секретный вектор ошибок веса wt(e)≤ t, содержащий секретную информацию. Вектор s по сути является синдромом. Абонент Х, получив вектор s, сначала находит какой-либо вектор b, который является решением уравнения xНт=s. Для этого требуется привести матрицу H к систематическому виду (In–k, Z), где In–k – единичная матрица с размерами (n–k) (n–k), а Z – матрица проверок с размерами (n–k) k. Очевидно, вектор b является вектором вида b=aE+e при некотором неизвестном a. Затем абонент Х декодирует вектор bP–1=b =a G+e , находит вектор e , а затем и вектор e=e P. В приведенном алгоритме декодирования не участвует матрица S, но ее необходимость обусловлена маскировкой матрицы H. Так как матрицы H и E связаны соотношением EHт=0, то в качестве открытого ключа можно рассматривать и матрицу H.

Стойкость рассмотренных систем во многом зависит от используемого помехоустойчивого кода, особенности которого могут быть использованы при реализации атак на шифросистемы.

117