
Теория Информации - Методичка (1 семестр)
.pdf
wth(1011010)=4, wth(1100110)=4, wth(1101001)=4, wth(1110000)=3, wth(1111111)=8}=3. Следовательно, рассматриваемый код гарантированно обнаруживает две, а исправляет 1 ошибку. 
5.5. Код Хемминга
Рассмотрим пример семейства известных блочных линейных кодов с минимальным расстоянием 3, т. е. кодов, способных исправлять одну или обнаруживать две ошибки в пределах одного кодового слова. Это коды Хемминга, известные с 1950 г. Их задают над произвольными полями, однако в данной главе мы ограничимся полем F2. Коды Хемминга являются совершенными.
Для кодов Хемминга рассмотрим специальные алгоритмы кодирования и декодирования. Идея построения простого декодера для этих кодов состоит в том, что код может быть представлен в таком виде, что значение синдрома будет равно номеру позиции, в которой произошла ошибка.
Итак, коды Хемминга представляют собой однопараметрическое семейство блочных бинарных кодов с параметром r = 2, 3, 4, … . Характеристики кода: длина n=2r –1, размерность k=2r–1–r, число проверочных символов r=n–k, минимальное кодовое расстояние d=3, количество гарантированно исправляемых ошибок на блок t=1. Проверочная матрица Нr,n кода Хемминга представляет собой (r n)-матрицу, столбцами которой являются все ненулевые двоичные векторы длиной n, записанные в естественном лексикографическом порядке.
Алгоритм кодирования кодом Хемминга заключается в сле-
дующем.
Выберем параметр r и вычислим значения n и k. Рассмотрим
сообщение à (à ,...à ) |
GFk(2). |
|
|
|
|||
1 |
k |
|
|
|
|
|
|
Построим |
вспомогательную матрицу |
Мn,r=(Hr,n)т |
порядка |
||||
(2r–1) r . |
|
|
|
|
|
|
|
|
|
|
|
F2n сле- |
|||
Структура искомого кодового слова b |
(b ,...,b ) |
||||||
|
|
|
|
|
1 |
n |
|
дующая: символы, индексы которых являются степенью двойки, т. е.
99
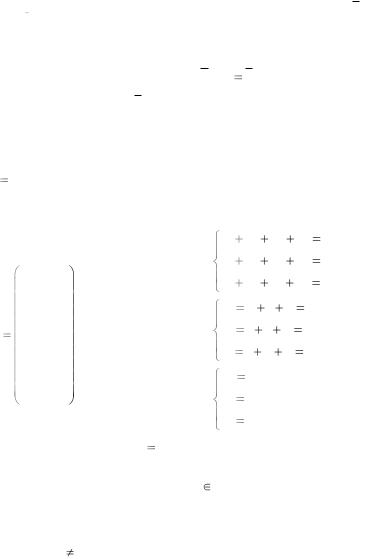
b20 ,b21 ,...,b2r 1 , – проверочные, а остальные символы вектора b
совпадают с буквами сообщения à , записанными в естественном порядке.
Рассмотрим систему уравнений bHn,r 0 и, используя из-
вестные координаты вектора b , вычислим значения r=n–k проверочных символов. В каждое из уравнений входит только один проверочный символ.
Пример 5.6. Рассмотрим случай r=3, n=7, k=4. Закодируем слово a 1010 . Для этого построим вспомогательную матрицу Н7,3, вычислим b3=1, b5=0, b6=1, b7=0, запишем и решим систему уравнений:
|
|
|
|
|
|
|
|
|
|
b4 |
b5 |
b6 |
|
b7 |
0, |
|
|
0 |
0 |
1 |
|
|
|
|
|
b2 |
b3 |
b6 |
|
b7 |
0, |
||
|
|
|
|
|
|
b1 |
b3 |
b5 |
|
b7 |
0, |
|||||
|
0 |
1 |
0 |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
0 |
1 |
1 |
|
|
|
|
|
b4 |
0 |
1 |
0 |
1, |
|
||
H7,3 1 |
0 |
0 |
|
|
|
|
|
b2 |
1 |
1 |
0 |
0, |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
1 |
0 |
1 |
|
|
|
|
|
b1 |
1 |
0 |
0 |
1, |
|
||
|
1 |
1 |
0 |
|
|
|
|
|
b4 |
1, |
|
|
|
|
||
|
1 |
1 |
1 |
|
|
|
|
|
b2 |
0, |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
b1 |
1. |
|
|
|
|
|
|
Отсюда получаем, что b 1011010 . |
|
|
|
|
|
||||||||||
|
Алгоритм декодирования можно представить в следующем |
|||||||||||||||
виде. Для полученного по каналу слова ñ |
Fn(2) вычислим: |
|
||||||||||||||
|
|
|
|
|
|
ñ Нn,r= ñ (Hr,n)т. |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|||||||
Если |
ñ Hn,r= 0 , |
то делаем вывод, что ñ = b – |
правильное кодовое |
|||||||||||||
|
|
|
|
|
|
с |
|
|||||||||
слово. |
Если |
ñ Мn,r 0 , то делаем вывод, |
что слово |
содержит |
||||||||||||
ошибку. Так как предполагается, что на блок попадает не более од-
100

ной ошибки, то вектор ошибок имеет вид: ei |
(0,0,...,1, ...,0,0) (1 – на |
|||||||||||||
i-м месте). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
В силу равенства ñ Hn,r=( b ei )Hn,r= ei |
Hn,r, |
делаем вывод, |
|||||||||||
что вектор |
ñ Hn,r представляет собой двоичную запись |
номера i, |
||||||||||||
указывающего на позицию ошибки. Вычисляем |
вектор ошибки |
|||||||||||||
e |
ei . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
Вычисляем правильное кодовое слово: b |
c |
e . |
|
||||||||||
|
|
|
|
|
|
|||||||||
|
По правильному кодовому слову b |
восстанавливаем сооб- |
||||||||||||
|
|
|
|
|
|
|||||||||
щение a , удаляя из b |
проверочные символы. |
|
|
|
||||||||||
|
Пример 5.7. Рассмотрим случай r=3, n=7, k=4. Предположим, |
|||||||||||||
на |
входе |
получено |
слово |
с =1010010. |
Вычисляем |
синдром |
||||||||
ñÌ |
7,3 (1,0,0) . Делаем вывод, |
что ошибка есть. По синдрому вычис- |
||||||||||||
ляем (1,0,0)2 |
410 и делаем предположение, что неправильно принят |
|||||||||||||
четвертый символ. Следовательно, b (1011010) , a (1010) .
Краткие итоги
Естественным способом построения множества кодовых слов является применение к информационным словам некоторой линейной операции: с=F(i).
Строки порождающей и проверочной матрицы содержат базисные векторы ортогональных пространств.
Универсальный декодер блочных линейных кодов основан на разбиении пространства Fqn на qn–k смежных классов.
Декодер кодов Хемминга проще универсального и основан на использовании возможности его особого представления таким образом, что значение синдрома равно номеру позиции, в которой произошла ошибка.
101
102
Рекомендуемая литература
1.Морелос-Сарагоса Р. Искусство помехоустойчивого кодирования. Методы, алгоритмы, применение / Р. Морелос-Сарагоса. –
М.: Техносфера, 2005. – 320 с.
2.Деундяк В.М. Семейство кодов Рида–Маллера и коды Хэмминга: метод. указания по курсу «Теория информации» / В.М. Деундяк, Н.С. Могилевская, Е.А. Степанюченко. – Ростов н/Д: Издательский центр ДГТУ, 2004. – 11 с.
3.Сидельников В.М. Теория кодирования / В.М. Сидельников. – М.: Физматлит, 2008. – 324 с.
4.Блейхут Р. Теория и практика кодов, контролирующих ошибки / Р. Блейхут. – М.: Мир, 2006. – 576 с.
5.Мак-Вильямс Ф. Дж. Теория кодов исправляющих ошибки / Ф. Дж. Мак-Вильямс, Н. Дж. Слоэн. – М.: Связь, 1979. – 744 с.
Набор для практики по теме «Матричное описание линейных блочных кодов»
Проверьте уровень освоения материала по теме «Матричное описание линейных блочных кодов», используя предложенные тесты.
Упражнения
Согласно выданному преподавателем варианту, дважды выполните типовое контрольное задание (см. ниже): один раз считая заданную матрицу М порождающей, другой раз – проверочной.
Выполнить описанные действия для двоичного линейного блочного кода, обладающего заданной порождающей (или проверочной) матрицей.
A.Вычислить длину, размерность и скорость кода.
B.Вычислить количество кодовых слов.
C.Найти порождающую и проверочную матрицы в систематическом виде заданного или эквивалентного кода.
103

D.Построить две таблицы, необходимые для работы лидерного декодера.
E.Рассчитать синдром для принятого из зашумленного канала вектора с и декодировать его, используя стандартную таблицу.
F.Выяснить способности рассматриваемого кода по исправлению и обнаружению ошибок.
|
|
1 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
|
1 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1) |
M= 0 1 1 1 0 1 0 0 ; |
5) M= 0 1 0 1 0 1 0 1 ; |
||||||||||||||||
|
|
0 |
0 |
1 |
1 |
1 |
0 |
1 |
0 |
|
0 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
|
|
0 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
|
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
2) |
M= |
1 |
0 |
|
1 |
1 |
0 |
|
; |
|
1 |
0 |
|
0 |
1 |
1 |
1 |
0 |
0 1 0 1 1 |
|
6) M= |
0 1 0 0 1 1 1 . |
|||||||||||||||
|
|
1 |
1 |
0 |
0 |
1 |
1 |
0 |
|
0 |
0 |
|
1 |
1 |
0 |
1 |
1 |
|
3) |
M= |
0 1 1 1 1 0 0 ; |
|
1 0 1 0 0 |
|
|
||||||||||||
|
|
0 1 1 0 0 1 1 |
7) M= |
1 1 0 1 0 |
|
|
||||||||||||
|
|
1 |
1 |
|
0 |
1 |
0 |
|
|
|
0 |
1 |
|
0 |
0 |
1 |
|
|
4) |
M= |
0 |
0 |
|
1 |
0 |
0 |
; |
|
|
1 |
0 |
|
1 |
1 . |
|
|
|
|
|
0 |
1 |
|
0 |
1 |
1 |
|
|
8) M= |
|
|
|
|||||
|
|
|
|
|
|
0 |
1 |
|
1 |
0 |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
Тесты |
|
|
|
|
|
|
|
|
|
|
Вариант 1 |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
1. Чему равно расстояние Хемминга между векторами |
||||||||||||||||
0011010101 и 1010010001? |
|
|
|
|
|
|
|
|
|
|||||||||
|
|
а) 3; |
|
|
б) 4; |
|
|
в) 10; |
г) невозможно определить. |
|
||||||||
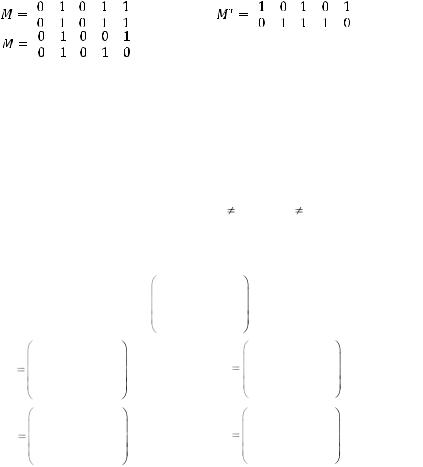
2. Какая из представленных матриц не может быть порождающей матрицей двоичного (4,2)-кода?
а) |
в) |
б) |
г) нет подходящей матрицы |
|
104

3. Код задан множеством кодовых слов {00000, 11111, 01110, 11000, 01111}. Чему равно минимальное кодовое расстояние этого кода?
а) 1; б) 0; в) 2; г) 3.
4. Выберите утверждение, верное для произвольного самодуального кода, заданного порождающее матрицей G = (I|P)?
а) I=P; б) P=Pт; в) I=Pт; |
г) P=Iт. |
||||||
5. Какая из представленных матриц не является эквивалент- |
|||||||
ной для порождающей матрицы: |
|
|
|
|
|
||
|
1 |
0 |
0 |
0 |
1 |
1 |
1 |
G |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
|
0 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
|
1 |
|
1 |
|
0 |
а) G 0 |
1 0 1 0 1 1 |
в) G 1 0 1 |
0 |
1 |
0 |
1 |
||||||||||
0 |
0 |
1 |
0 |
0 |
0 0 |
1 |
1 |
1 |
1 |
|
0 |
|
0 |
|
0 |
|
1 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
|||
б) G 1 1 |
0 |
1 |
0 |
1 |
0 |
г) G 0 |
1 |
0 1 0 1 1 |
||||||||
1 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
|||
6. Сколько кодовых слов в троичном коде, заданном проверочной матрицей
|
1 |
0 |
0 |
0 |
1 |
1 |
1 |
H |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
|
0 |
0 |
1 |
1 |
1 |
0 |
1 |
а) 16; б) 81; в) 27; г) 8.
7. Сколько ошибок может исправить код, заданный матрицей:
G = 1 |
0 |
1 |
1 |
0 |
? |
0 |
1 |
0 |
1 |
1 |
|
а) 0; б) 1; |
|
в) 1,5; |
|
г) 2. |
|
104
Вариант 2
1. Чему равно расстояние Хемминга между векторами
02100120 и 01100100? |
|
а) 2; б) невозможно определить; в) 3; |
г) 8. |
2. Какая из представленных матриц yt может быть порождающей матрицей двоичного (5,2)-кода?
а) |
в) |
б) |
г) нет подходящей матрицы |
|
3. Код задан множеством кодовых слов {00000, 11111, 01110, 11001}. Чему равна скорость этого кода?
а) 2/5; б) невозможно определить; в) 4/5; г) 5/2.
4. При выполнении какого из утверждений код, заданный порождающей матрицей G=(I|P) гарантированно не будет самодуальным?
а) I=P; б) P=Pт; в) I Pт; г) P Pт.
5. Какая из представленных матриц не является эквивалентной для порождающей матрицы:
1 |
0 |
1 |
0 |
0 |
|
G= 1 |
1 |
0 |
1 |
0 |
? |
0 |
1 |
0 |
0 |
1 |
|
0 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
а) G 1 |
1 |
0 |
1 |
0 |
в) G 0 1 0 1 0 |
||||
1 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
б) G 1 0 0 1 1 |
г) G 0 |
1 |
1 |
1 |
0 |
||||
0 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
105

6. Сколько кодовых слов в троичном коде, заданном проверочной матрицей:
1 |
0 |
1 |
0 |
0 |
|
H= 1 |
1 |
0 |
1 |
0 |
? |
0 |
1 |
0 |
0 |
1 |
|
а) 16; б) 81; в) 27; г) 8.
7. Сколько ошибок может исправить код, заданный матрицей
|
1 |
0 |
1 |
0 |
0 |
|
G = |
1 |
1 |
0 |
1 |
0 |
? |
|
0 |
1 |
0 |
0 |
1 |
|
а) 0; |
б) 1; |
в) 1,5; |
г) 2. |
|||
Вариант 3
1. Чему равно расстояние Хемминга между векторами
02100120 и 011001000?
а) 3; б) невозможно определить; в) 2; г) 4.
2. Какая из представленных матриц может быть проверочной
матрицей двоичного (5,3)-кода? |
|
а) |
в) |
|
|
б) |
г) нет подходящей матрицы |
|
3. Код задан множеством кодовых слов {00000, 11111, 01110, 11001}. Чему равна избыточность этого кода?
а) 2/5; б) невозможно определить; в) 5/4; г) 5/2.
106

4. При выполнении какого из равенств двоичный код, заданный порождающей матрицей H=(Pт|I) гарантированно не будет самодуальным?
а) I=P; б) P=Pт; в) I Pт; г) P=Iт.
5. Известно, что код С задан порождающей матрицей:
H= |
1 |
1 |
0 . |
|
1 |
0 |
1 |
Какое из утверждений является верным при любых значениях других параметров кода?
а) это двоичный код |
|
|
в) этот код исправляет ошибки |
|||
б) это (3,1)-код |
|
|
г) это самодуальный код |
|||
6. Сколько кодовых слов в троичном коде, заданном прове- |
||||||
рочной матрицей: |
|
|
|
|
|
|
H= |
1 |
1 |
0 |
0 |
1 |
? |
|
1 |
0 |
1 |
0 |
0 |
|
а) 8; |
б) 4; |
в) 27; |
г) 9. |
|||
7. Сколько ошибок может исправить код, заданный матри- |
||||||
цей: |
|
|
|
|
|
|
G = |
1 |
1 |
0 |
1 |
0 |
? |
|
1 |
1 |
0 |
1 |
0 |
|
а) 1 |
|
|
в) 1,5 |
|
|
|
б) ни одной |
|
|
г) эта матрица не может быть по- |
|||
|
|
|
рождающей матрицей кода |
|||
107
