
Теория Информации - Методичка (1 семестр)
.pdfОтметим, что согласованные пары кодеров-декодеров принято называть кодеками. Система передачи оптимальна, если кодер источника осуществляет максимальное сжатие с допустимым уровнем потерь в качестве, а цифровой канал обеспечивает максимальную скорость достоверной передачи при известных характеристиках помех. В этом случае уменьшение избыточности входного сообщения осуществляется кодеком источника, а уменьшение вероятности ошибки в полученном по каналу сообщении – кодеком канала. Таким образом, для создания эффективной и экономичной системы связи необходимо уметь согласовывать характеристики возможных помех в канале и выбор кодеков источника и канала. Подробнее методы подбора помехоустойчивых кодеков к каналам с известными характеристиками приведены в учебном пособии [3].
Уточним еще раз используемые термины. Так, кодом называют правило (алгоритм) по которому каждому конкретному информационному сообщению ставится в соответствие строго определенная комбинация символов (знаков). Кодом также называется отдельная последовательность таких символов (знаков) – кодовое слово.
Процесс преобразования информационного сообщения в кодовое слово в соответствии с кодом называется кодированием, процесс восстановления сообщения из кодового слова называется декодированием.
Далее будут рассмотрены материалы, связанные с выделенными в схеме (см. рис. 1.1) элементами системы связи. В этой главе мы рассмотрим источники сообщений и научимся оценивать количество информации независимых событий.
1.2. Дискретный источник сообщений
Введем некоторые необходимые обозначения и определения. Пусть 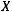 – некоторое дискретное множество, содержащее конечное множество элементов
– некоторое дискретное множество, содержащее конечное множество элементов 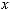

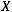 . Элементы
. Элементы 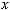
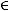
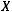 назовем элементарными событиями. Запись
назовем элементарными событиями. Запись 
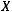
 будем использовать для обозначения мощности множества
будем использовать для обозначения мощности множества  , т.е. для обозначения количества
, т.е. для обозначения количества
9
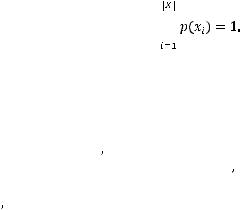
символов, которые алфавит  содержит. Пусть
содержит. Пусть 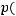
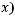 обозначает вероятность появления события
обозначает вероятность появления события  . Тогда множество чисел {
. Тогда множество чисел { 
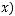 }, где
}, где 
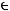
 , задает распределение вероятностей на дискретном множестве
, задает распределение вероятностей на дискретном множестве  , если все числа
, если все числа 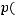
 неотрицательны и для них справедливо следующее условие:
неотрицательны и для них справедливо следующее условие:
В теории информации часто используется следующая терминология: множество  называют алфавитом, а его элементы – символами или буквами алфавита. Последовательности букв алфавита, записанные друг за другом, принято называть словами.
называют алфавитом, а его элементы – символами или буквами алфавита. Последовательности букв алфавита, записанные друг за другом, принято называть словами.
Алфавит 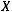 в совокупности с распределением вероятностей
в совокупности с распределением вероятностей
{ 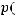
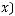 }, где
}, где 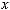
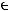
 называется вероятностной схемой или дискретным вероятностным ансамблем
называется вероятностной схемой или дискретным вероятностным ансамблем 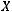

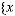
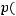
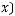
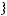 .
.
Назовем простейшим дискретным источником без памяти
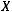 некоторое устройство, которое в каждый фиксированный момент времени
некоторое устройство, которое в каждый фиксированный момент времени 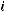 выдает некоторый символ
выдает некоторый символ 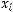
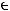
 из конечного алфавита
из конечного алфавита 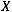 с вероятностью
с вероятностью 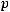


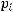
 Выборки символов производятся независимо друг от друга.
Выборки символов производятся независимо друг от друга.
Поясним основные термины этого определения. Так слово «простейший» указывает на чрезвычайную простоту источника, слово «дискретный» подчеркивает факт работы с конечным дискретным алфавитом 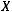 . А выражение «без памяти» говорит о том, что в каждый момент времени
. А выражение «без памяти» говорит о том, что в каждый момент времени 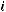 источник выдает новый символ
источник выдает новый символ 
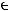
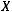 независимо от тех символов, которые он выдал ранее, т. е. говоря простыми словами, источник не помнит, что он выдал нам раньше.
независимо от тех символов, которые он выдал ранее, т. е. говоря простыми словами, источник не помнит, что он выдал нам раньше.
Пример 1.1. Рассмотрим в качестве двоичного источника сообщений результаты подбрасывания «честной» монеты (т.е. монеты для которой выпадение орла или решки равновероятно). Обозначим х0 событие «орел», а х1 – «решка». Тогда Х={х0, х1}, p0=p1=0,5. 
Существуют ли более сложные источники сообщений? Конечно да. Но на данном этапе, нам вполне достаточно такого представления об источнике сообщений.
10
Пример 1.2. Рассмотрим одиночные события. Повседневный опыт подсказывает, что часто происходящие события так же, как и их вероятности, дают нам мало информации. Возьмем, например, сообщение «Человека укусила собака». Это довольно-таки привычное известие привлекло бы к себе мало внимания, в то время как сообщение «Человек укусил собаку» газеты написали бы крупным шрифтом. Или, «вершина горы Чигета 1 июля покрыта снегом» – обычное событие, «1 июля в Ростове-на-Дону лежит снег» – необычное явление, дающее нам большое количество информации.
Из рассмотренного примера можно сделать вывод, что информация и вероятность находятся в обратной пропорциональной зависимости.
1.3. Количество информации, энтропия
Очевидно, что в качестве строгого научного понятия, информацию нужно рассматривать как измеряемую величину (как длину в метрах, время в секундах). Введем понятие количества информации как измеряемой величины на основании трех аксиом, которые впервые ввел Клод Шеннон.
Аксиомы для определения количества информации:
– информация одиночного события
, |
происходящего |
с |
вероят- |
|
|
|
|
|
|
|
|
|
|
Шеннон |
не |
только |
|||||||||
ностью |
имеет неотрицательное значе- |
|
||||||||||
положил начало |
теории |
|||||||||||
ние |
|
|
|
информации, |
это |
|
|
чело- |
||||
|
|
|
век, который придумал |
|||||||||
– совместная информация двух не- |
||||||||||||
бит. |
|
|
|
|
|
|
||||||
зависимых событий |
с совместной |
|
Он |
определил |
ос- |
|||||||
новную единицу количе- |
||||||||||||
вероятностью |
|
рав- |
||||||||||
|
ства |
информации |
как |
|||||||||
на сумме |
их информаций: |
|
сообщение, |
представля- |
||||||||
|
ющее один из двух вари- |
|||||||||||
|
|
|
|
|||||||||
|
|
|
|
антов, |
|
например, |
||||||
– информация является непре- |
0 или 1, «да» или «нет». |
|||||||||||
Название bit |
произошло |
|||||||||||
рывной функцией от вероятности собы- |
от слов binary digit. |
|
|
|||||||||
|
|
|
|
|
|
|
|
|||||
тия.
11

Из аксиом видно, что информация нескольких событий взаимно не уничтожается; аксиома о совместной информации показывает, что информация события определяется как логарифмическая
функция вероятности. |
|
Информация события хi, происходящего с вероятностью |
|
. |
(1.1) |
В формуле (11) не указано основание логарифма. Значение основания логарифма влияет на единицу измерения информации. Так, при использовании логарифма по основанию 2 единицей информации будет бит, при использовании натурального основания единицей измерения будет нат. Десятичный логарифм даст нам – дит или Хартли. Далее, если не будет указано иное, будем считать, что информация измеряется в битах.
|
Формально верной записью для информации будет |
|
, однако для краткости обычно используют запись |
или |
Кроме этого, заметим, что формально в определении [см. |
формулу (1.1)] нужно говорить не об информации события, а о количестве информации, которое мы получаем, когда происходит указанное событие.
Пример 1.3. Пусть Х={a, b, c}, вероятности появления событий: p(a)=1/2, p(b)=1/4, p(c)=1/4. Вычислим количество информации в этих событиях: I(a)=1 бит, I(b)=I(c)=2 бит.
Еще одной мерой, связанной с информацией является энтропия. Не прибегая к точной формулировке, можно сказать, что энтропия показывает, насколько трудно верно угадать результат како- го-либо события. Рассмотрим несколько ситуаций. Представьте, что Вам нужно угадать, кем будет первый встреченный Вами человек на улице: левшой или правшой? Чаще всего Вы будете угадывать верно. Если Вам нужно будет сказать, окажется ли этот человек мужчиной или женщиной, то угадывать Вы будете реже, чем в предыдущем случае. Еще реже Вы будете верно угадывать цвет волос и уж совсем редко верно сможете назвать размер ноги этого человека.
12

А уж если перейти к угадыванию верных комбинаций в лотерейных билетах, то шансы на верный ответ практически стремятся к нулю.
Для практики важно уметь количественно оценивать степень неопределенности различных событий, чтобы уметь сравнивать их между собой. В теории информации для определения меры неопределенности используется энтропия.
Энтропия |
простейшего |
источника без памяти с алфави- |
том |
и |
соответствующими вероятностям |
появления символов алфавита
Как и в случае определения количества информации, основание логарифма влияет на единицу измерения энтропии. Энтропию можно рассматривать как количественную меру неосведомленности о том, какое сообщение будет порождено источником сообщений. Чем значение энтропии больше, тем сложнее угадать, какое событие произойдет, и наоборот.
Пример 1.4. Пусть источник сообщений Х выдает символы из алфавита Х={a, b, c} с вероятностями: p(a)=1/2, p(b)=1/4, p(c)=1/4.
Вычислим энтропию этого источника:
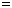
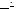


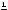

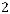

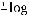
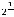

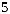 бит.
бит. 
1.4. Аксиоматическое определение энтропии
Многие исследователи определяют энтропию с аксиоматических позиций. Обычно различные системы аксиом практически эквивалентны друг другу. Согласно образовательному стандарту, нам нужно рассмотреть аксиомы Хинчина и Фаддеева.
13

А.Я. Хинчин показал, что энтропия конечной вероятностной схемы может быть однозначно определена с точностью до постоянного множителя при задании следующей системы аксиом.
|
|
Аксиомы Хинчина |
|
|
|
|
|
|
|
1. |
|
– ненулевая непрерывная функция веро- |
|||||||
|
|
ятностей |
|
при этом |
и |
||||
Функция |
называется |
|
|
|
|
|
|
|
|
симметрической, если |
2. |
|
|
|
– симметрическая |
||||
x, y : f(x,y) = f(y,x). |
|
|
|
||||||
по переменным |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
||
3. |
|
|
|
|
|
|
|
|
|
4. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5. |
|
|
|
|
|
|
. |
|
|
|
|
||||||
Система аксиом Фаддеева эквивалентна системе аксиом |
||||||||
Хинчина и позволяет получить тот же результат. |
|
|||||||
|
|
|
Аксиомы Фаддеева |
|
||||
1. |
|
|
непрерывна при |
и положительна |
||||
|
|
|||||||
хотя бы в одной точке. |
|
|
|
|
|
|
||
2. |
|
|
– симметрическая |
по переменным |
||||
3. При 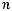
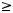
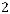
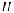
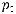
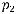

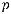
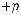
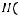
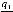
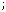
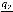
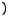 , где
, где 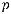
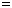
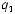

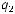

Альтернативная формулировка аксиомы 3 Фаддеева и 4 Хинчина может звучать так: способ выбора событий не изменяет энтропию.
14
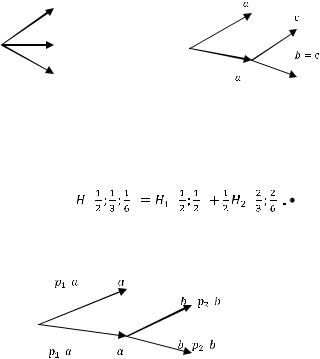
Рассмотрим пример, иллюстрирующий постоянство значения энтропии вне зависимости от способа выбора событий, а затем в общем виде докажем справедливость альтернативной формулировки аксиом о постоянстве энтропии.
Пример 1.5. Пусть необходимо выбрать один символ из алфавита {a, b, c} c вероятностями 1/2, 1/3 и 1/6. Один символ можно выбрать различными способами. Например, за один шаг (рис. 1.2, а) или за два шага, сначала отбросить один из символов, а затем выбрать один из двух оставшихся (рис. 1.2, б).
|
a |
1/2 |
|
1/2 |
2/3 |
||
|
|||
1/3 |
b |
|
|
|
|
||
1/6 |
|
1/3 |
|
c |
|
||
|
1/2 |
||
|
|
||
а) |
|
б) |
Рис. 1.2. Примеры способов выбора события из множества
Согласно рассматриваемым аксиомам, должно выполняться равенство:
Покажем в общем виде, что определение энтропии удовлетворяет этой аксиоме (рис. 1.3).
Рис. 1.3. Разложение процедуры выбора события на ряд двоичных решений
15

Для разложенной энтропии получаем:
очевидно, что выполняются следующие равенства:
Подставляя указанные равенства в формулу энтропии, полу-
чаем:
После упрощения:
Пятая аксиома Хинчина
показывает, что энтропия достигает максимума в случае равновероятных событий. Рассмотрим теорему, подтверждающую эту аксиому.
Теорема о максимальной емкости источника. Энтропия простейшего источника без памяти Х максимальна, если все события, в нем содержащиеся, имеют одинаковую вероятность. В этом случае энтропия равна логарифму событий

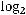
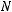 , где
, где 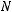

16
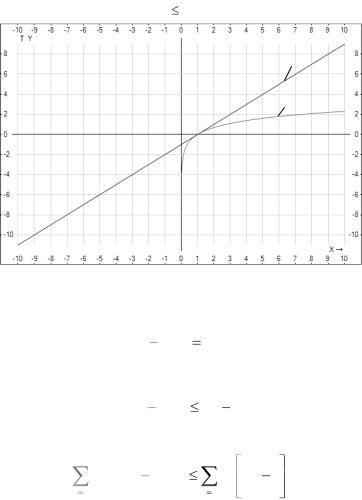
Доказательство.
Рассмотрим два дискретных источника без памяти Р и Q, таких, что |P|=|Q|=N, pi=qi=1/N, где pi, qi – вероятности событий источников P и Q соответственно. Используем известную логарифмическую оценку (рис. 1.4):
ln x x – 1.
2
1
Рис. 1.4. Графики функций: 1 – f = lnx; 2 – g = x – 1
Используя известное логарифмическое равенство, запишем:
ln q |
ln p |
ln |
qi |
, |
|
|
|||||
i |
i |
|
pi |
||
|
|
|
|||
следовательно, |
|
|
|
|
|
ln qi |
ln pi |
qi |
1. |
||
pi |
|||||
|
|
|
|
||
Умножим обе части неравенства на pi и просуммируем по всем i:
N |
N |
qi |
|
|
pi ln qi ln pi |
pi |
1 . |
||
pi |
||||
i 1 |
i 1 |
|
17
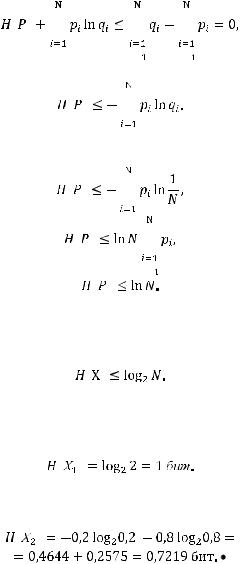
Упростим выражение:
перенесем сумму вправо:
Пусть источник  содержит только равновероятные события, тогда
содержит только равновероятные события, тогда
Так как в ходе доказательства на источник  не было наложено каких-либо ограничений, то данное доказательство действительно для любого дискретного источника без памяти, содержащего
не было наложено каких-либо ограничений, то данное доказательство действительно для любого дискретного источника без памяти, содержащего 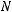 событий
событий
Неравенство превращается в равенство, если все события в 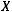 равновероятны.
равновероятны.
Пример 1.6. Вычислим энтропию двоичного источника 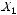 , в случае равновероятных событий:
, в случае равновероятных событий:
Вычислим энтропию двоичного источника 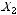 , в случае если события алфавита происходят с вероятностями 0,2 и 0,8 равновероятных событий:
, в случае если события алфавита происходят с вероятностями 0,2 и 0,8 равновероятных событий:
18
