- •Раздел I. Физические основы механики.
- •I закон Ньютона
- •II закон Ньютона
- •III закон Ньютона
- •II. Типы деформаций. Основные характеристики деформаций.
- •III. Напряжение. Связь между деформацией и напряжением. Закон Гука.
- •Раздел II. Основы молекулярной физики и термодинамики.
- •Раздел III. Электрическое поле.
- •Раздел IV. Магнитное поле.
- •1. 2. Графическое изображение магнитного поля. Поток вектора магнитной индукции
- •1. 3. Закон Био-Савара-Лапласа и его применение
- •1. 4. Циркуляция вектора индукции магнитного поля по замкнутому контуру. Вихревой характер магнитного поля
- •1. 5 Теорема Остроградского-Гаусса для магнитного поля
- •1. 6 Действие магнитного поля на токи и заряды
I закон Ньютона
Существуют такие системы отсчета, которые называются инерциальными, относительно которых тела сохраняют свою скорость неизменной, если на них не действуют другие тела или действие других сил скомпенсировано.
Тело (материальная точка), не подверженное внешним воздействиям, либо находится в покое, либо движется прямолинейно и равномерно. Такое тело называют свободным. Движение такого тела называется свободным движением или движением по инерции.
Существует система отсчета, в которой все свободные тела движутся прямолинейно и равномерно.
ИЛИ
Существуют такие системы отсчёта, называемые инерциальными, относительно которых материальная точка при отсутствии внешних воздействий сохраняет величину и направление своей скорости неограниченно долго.
Такие системы называется инерциальными системами отсчета (Первый закон Ньютона).
Неинерциальная система отсчёта — система отсчёта, в которой не применим первый закон Ньютона — «закон инерции», говорящий о том, что каждое тело, в отсутствие действующих на него сил, движется по прямой и с постоянной скоростью. Всякая система отсчета, движущаяся с ускорением или поворачивающаяся относительно инерциальной, является неинерциальной.
II закон Ньютона
Ускорение
тела прямо пропорционально равнодействующей
сил, приложенных к телу, и обратно
пропорционально его массе:
![]()
Физическая величина, равная произведению массы тела на скорость его движения, называется импульсом тела (или количеством движения). Импульс тела – векторная величина. Единицей измерения импульса в СИ является килограмм-метр в секунду (кг·м/с).Физическая величина, равная произведению силы на время ее действия, называется импульсом силы. Импульс силы также является векторной величиной. Второй закон Ньютона может быть сформулирован следующим образом: изменение импульса тела (количества движения) равно импульсу силы. Обозначив импульс тела буквой p второй закон Ньютона можно записать в виде
|
Масса является мерой инертности тела. Чем меньше ускорение, которое получает тело, тем больше его масса, т.е. ускорения тел обратно пропорциональны их массам. Приняв какую-либо массу за эталон, с помощью этого соотношения можно измерять любую массу.
III закон Ньютона
Силы,
с которыми два тела действуют друг на
друга, равны по модулю и противоположны
по направлению.
![]()
Сила, с которой тела притягиваются к Земле вследствие гравитационного взаимодействия, называется силой тяжести. Согласно закону всемирного тяготения
Форума
Fтяж=G mM/R2 Или F=mg где g — ускорение свободного падения, R — расстояние от центра Земли до тела, М — масса Земли, т — масса тела. Движение тела под действием только силы тяжести называют свободным падением. Свободное падение происходит с ускорением g, которое, как показано выше, не зависит от массы тела. Вблизи поверхности Земли g = 9,8 м/с2, по мере удаления от Земли эта величина убывает. Весом тела называют силу, с которой тело действует на опору или подвес вследствие притяжения к Земле. Вес тела Р, в отличие от силы тяжести, приложен не к данному телу, а к его опоре или подвесу.
Лекция 3. Работа, мощность, энергия. Законы сохранения энергии и импульса.
Для упрощения изложения; 1. Скорости тел значительно меньше скорости света. 2. Силы, вызванные сопротивлением среды, не учитываются (диссипативные силы, которые всегда отрицательные). 3. Действия, сложения и умножения над скалярами и векторами и между ними , по умолчанию. 4. Единицы силы "F" (обзор системы СИ) – 1Н (ньютон) проявляется при движении массы - тела с ускорением и вычисляется, кг*(м/сек^2) 1Н=1кг(массы)*(м/сек^2), F = кг* м/сек^2 =H Сила величина векторная, она может быть положительной и отрицательной. 5. Сила всегда совершает работу - "А", она является мерой передачи движения от одного тела к другому. Работа величина алгебраическая, она может быть положительной и отрицательной А=Fs – путь пройденный телом под воздействием силы F. А= Fs =кг*(м/сек^2)*м= кг* м^2/сек^2= Н*м = Дж Вектор силы может не совпадать с вектором скорости. А=Fs cos α. Где α- угол между векторами силы-F и направлением пути -s Работа – величина алгебраическая и может быть положительная (cos α >0) и отрицательная cos α <0 При вращательном движении, при повороте на угол φ, и в случае постоянного момента сил М, работа равна A=M φ 6. Мощность "N" – Это работа силы, совершаемая в единицу времени (величина скалярная) N= A/t = F* (скорость) = Н*м/сек = Fs /t = (кг*м^2/сек^2)/ сек =1Вт = Дж/сек Как видно, при падении тела мощность его массы увеличивается со скоростью, но мощность при упругом ударе может возрасти на несколько порядков. Это не означает, что не соблюдаются законы сохранения. Это типа рычага, сила возросла за счёт падения скорости. Как видно, мощность развиваемая массой в основном зависит от времени её реализации, временем взаимодействия масс (удар). 7. Энергия (величина скалярная) различается на кинетическую энергию и потенциальную. Полной механической энергией системы называется сумма кинетических и потенциальных энергий всех частиц входящих в эту систему. 8. Кинетическая энергия – физическая величина, определяемая работой, которую должны совершить силы при торможении движущегося тела. По сути, эта величина – виртуальная (отражает субъективную реальность). Ек = (m v^2)/2= (кг*м^2/сек^2)/2= 1 Дж= Вт*сек Кинетическая энергия является количественной мерой механического движения материальной точки (частицы). Кинетическая энергия тела, есть сумма кинетических энергий частиц его составляющих. 9. Потенциальная энергия является мерой положения материальной точки (частицы) в стационарном, потенциальном поле сил и определяется с точностью до постоянной величины (отражение объективной реальности). В физике принято считать потенциальную энергию сил притяжения – отрицательной, а потенциальную энергию сил отталкивания - положительной. Еп = - *M*m/R = - [(6.67*10^-11м^3 /кг*сек^2)*кг^2] /м = Дж Сравните сила тяготения F= *M*m/R^2= [(6.67*10^-11м^3 /кг* сек^2 ) *кг ^2 ] / м^2= Н Еп = mgh =(кг*м^2)/сек^2= Н*м= Дж Где, - гравитационная постоянная. 10. Поле сил - область пространства, где обнаруживается действие сил, изменяющихся по определённому закону. Независимое от времени поле сил называет стационарным. По условию -2, рассматриваемые поля потенциальные, а силы консервативные; силы тяжести, кулоновские силы. В этих полях, работа сил при перемещении между двумя любыми точками не зависит от формы пути, а зависит лишь от положения этих точек. 11. Закон сохранения МЕХАНИЧЕСКОЙ ЭНЕРГИИ: в инерциальной системе отсчёта механическая энергия замкнутой системы, в которой НЕТ диссипативных сил, остаётся постоянной в процессе движения. 12. В общем случае, энергией называется единая количественная мера различных форм движения (не только механических). 13. энергия не создаётся и не уничтожается; она может переходить из одной формы в другую; возможен обмен энергией между различными частями материи.
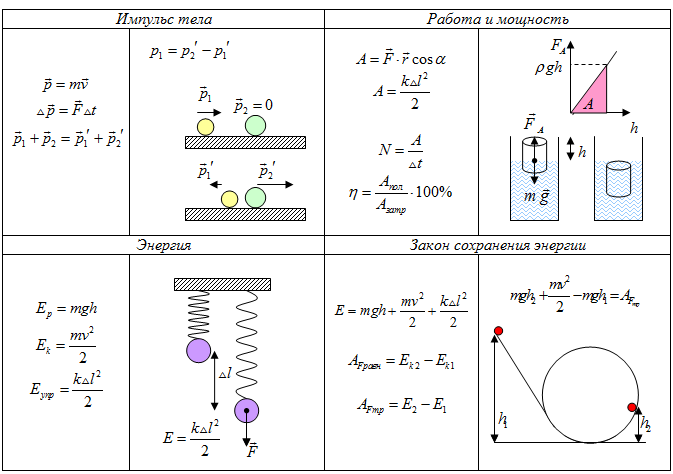
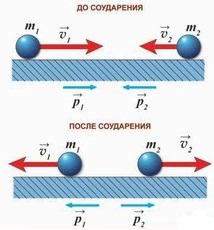
Закон сохранения импульса — Векторная сумма импульсов двух тел до взаимодействия равна векторной сумме их импульсов после взаимодействия
![]()
![]()
Лекция 4. Динамика вращательного движения твердого тела.
Момент инерции материальной точки,
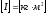
Момент
инерции
м.т. ( )
относительно полюса – скалярная
величина, равная произведению массы
этой точки на квадрат расстояния до
полюса:
)
относительно полюса – скалярная
величина, равная произведению массы
этой точки на квадрат расстояния до
полюса:
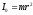 (1)
(1)
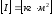
(2)
Момент инерции системы материальных точек
Тело можно представить состоящим из большого числа м.т., тогда момент инерции системы м.т. равен:
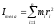 ,
(3)
,
(3)
где
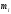 - массаi
- ой м.т.
- массаi
- ой м.т.
 -
ее расстояние до полюса О.
-
ее расстояние до полюса О.
Моментом инерции системы м.т. или тела относительно полюса называют алгебраическую сумму произведений масс м.т., из которых состоит тело, на квадрат расстояния их до полюса О.
Теорема Штейнера
Для установления связи между моментом инерции тел относительно двух параллельных осей применяется теорема Штейнера:
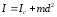 (4)
(4)
где
 - момент инерции относительно новой оси
- момент инерции относительно новой оси
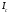 -
момент инерции относительно центра
масс
-
момент инерции относительно центра
масс
d – расстояние между осями
Момент силы,

Вектором момента силы относительно полюса называют векторное произведение радиус-вектора и вектора силы:
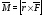 (5)
(5)
Направление
вектора момента силы находится по
правилу правого винта (см. рис): перенесем
вектор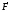 параллельно самому себе так, чтобы
совпадали начала векторов
параллельно самому себе так, чтобы
совпадали начала векторов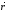 и
и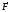 .
Если вращать головку винта в направлении
от вектора
.
Если вращать головку винта в направлении
от вектора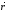 к вектору
к вектору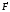 ,
то поступательное движение винта укажет
направление вектора момента силы
,
то поступательное движение винта укажет
направление вектора момента силы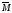 .
.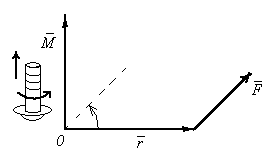
Модуль вектора момента силы равен:
 ,
(6)
,
(6)
где
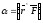 - угол между радиус-вектором и линией
действия силы.
- угол между радиус-вектором и линией
действия силы.
Момент равнодействующей силы относительно полюса О равен геометрической сумме векторов моментов составляющих сил относительно того же полюса:
 (7)
(7)
или
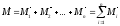 (8)
(8)
Момент импульса материальной точки,
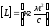
Вектором
момента импульса м.т. относительно
полюса О называют векторное произведение
радиус – вектора
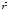 и вектора импульса
и вектора импульса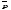 относительно
этого же полюса.
относительно
этого же полюса.
Радиус-вектор
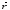 проводится
от полюса О до м. т.
проводится
от полюса О до м. т.
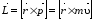 (9)
(9)
Направление вектора момента импульса находится по правилу правого винта и совпадает с вектором угловой скорости.
Если
учесть, что
 ,
тогда момент импульса равен:
,
тогда момент импульса равен: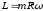
или
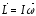 (10)
(10)
Момент количества движения твердого тела относительно оси вращения равен произведению момента инерции тела относительно той же оси на угловую скорость.
Модуль вектора момента импульса равен:
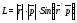 ,
(11)
,
(11)
Вектор момента импульса системы м.т. от-но полюса О равен геометрической сумме векторов моментов импульса, действующих на каждую точку в отдельности от-но того же полюса О:
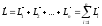 (12)
(12)
или

Согласно уравнению (5.8) второй закон Ньютона для вращательного движения
![]()
По
определению угловое ускорение ![]() и
тогда это уравнение можно
и
тогда это уравнение можно
переписать следующим образом
![]()
с учетом (5.9)
![]()
или
|
|
(5.10) |
Это
выражение носит название основного
уравнения динамики вращательного
движения и формулируется следующим
образом: изменение момента количества
движения твердого тела ![]() ,
равно импульсу момента
,
равно импульсу момента![]() всех
внешних сил, действующих на это тело.
всех
внешних сил, действующих на это тело.
Лекция 5. Закон сохранения момента импульса.
Момент импульса вращающегося тела
![]() , (1.47)
, (1.47)
где ![]() –
масса тела;
–
масса тела;![]() –
скорость;
–
скорость;![]() –
радиус орбиты, по которой перемещается
тело;
–
радиус орбиты, по которой перемещается
тело;![]() –
момент инерции;
–
момент инерции;![]() –
угловая скорость вращающегося тела.
–
угловая скорость вращающегося тела.
Закон сохранения момента импульса:
– для вращательного движения
![]() при
при ![]() ;
;
закон сохранения импульса:
– для поступательного движения
![]() при
при ![]() .
.
Для того чтобы изменить скорость при поступательном движении, необходимо обязательно приложить силу.
Угловую скорость можно изменить, не прикладывая силы или момент силы, достаточно изменить момент инерции. Так, фигурист, прижимая руки к телу, уменьшает момент инерции и его угловая скорость увеличивается.
Если,
например, в замкнутой системе у
вращающегося тела момент инерции
уменьшится до величины ![]() ,
то скорость вращения этого тела возрастет
(станет
,
то скорость вращения этого тела возрастет
(станет![]() 1,),
т. е.
1,),
т. е.
![]() . (1.48)
. (1.48)
Выражение (1.48) является законом сохранения момента импульса.
При вращательном движении скорость изменения момента импульса материальной точки равна моменту силы (при неизменном моменте инерции)
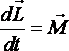 . (1.49)
. (1.49)
Наряду с законами сохранения импульса и энергии, закон сохранения момента импульса является одним из важнейших фундаментальных законов физики.
Важным
случаем является вращение твердого
тела вокруг неподвижной оси. В этом
случае момент инерции ![]() при
вращении остается постоянным и уравнение
(1.49) переходит в
при
вращении остается постоянным и уравнение
(1.49) переходит в
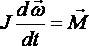 .
.
При уменьшении момента инерции вращающегося тела его угловая скорость увеличивается (при условии, что момент внешних сил равен нулю). Изменение угловой скорости системы может происходить только за счет работы каких-то сил. Такими силами в нашем примере являются внутренние силы, действующие в системе.
Отметим свойства замкнутой системы, на которую не действуют внешние силы. Если такая система покоится, то за счет внутренних движений (внутренних сил) эту систему невозможно сместить в пространстве (поступательное перемещение).
С помощью одних только внутренних движений можно повернуть систему в пространстве на любой угол [1].
Полагаем,
что под действием момента силы ![]() тело
с моментом инерции
тело
с моментом инерции ![]() вращается
с угловым ускорением
вращается
с угловым ускорением ![]() (
(![]() ). За
время
). За
время ![]() угловая
скорость изменилась на величину
угловая
скорость изменилась на величину ![]() –
тогда из основного закона динамики
вращательного движения следует
–
тогда из основного закона динамики
вращательного движения следует
![]() . (1.50)
. (1.50)
Импульс момента внешних сил, действующих на вращающееся тело, равен изменению его момента импульса.
Величина ![]() для
вращательного движения является
кинетической энергией. Выражение,
аналогичное для поступательного движения
записывается следующим образом:
для
вращательного движения является
кинетической энергией. Выражение,
аналогичное для поступательного движения
записывается следующим образом:
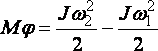 , (1.51)
, (1.51)
где![]() –
угловой путь, пройденный при воздействии
на тело момента сил
–
угловой путь, пройденный при воздействии
на тело момента сил![]() ;
;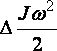 –
изменение кинетической энергии.
–
изменение кинетической энергии.
Лекция 6. Элементы механики сплошных сред.
Закон Паскаля.
Если пренебречь вначале силами тяготения, действующими на каждую частицу жидкости (или силами инерции, если таковые существуют), то из простейших соображений относительно условий равновесия элемента жидкости следует, что
|
p11 = p22 = p33 = p, |
(2.1) |
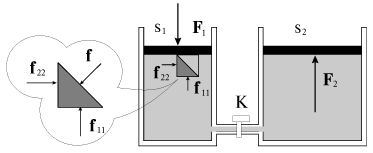
при этом давление p, являющееся скалярной величиной, одинаково во всех точках объема, занятого покоящейся жидкостью. Условие (2.1) автоматически обеспечивает не только равенство нулю суммы сил давления, приложенных к данному элементу, но равенство нулю суммарного момента этих сил. Для его доказательства рассмотрим неподвижную жидкость, помещенную в цилиндрический сосуд сечением S1, закрытый сверху поршнем (рис. 2.1, левый сосуд). Если надавить на поршень с силой F1, то в жидкости будут созданы внутренние напряжения (давления). На единицу поверхности элемента жидкости будет действовать сжимающая сила fii = - piini, направленное противоположно внешней нормали ni к i-ой поверхности (на рис. 2.1 изображены только две силы).
|
|
|
Рис. 2.1. |
Поскольку
силы, действующие на противоположные
грани кубика, равны по величине, то
p11=F1/S1.
Равенство давлений p11 и
р22 следует
из условия равновесия половины кубика,
выделенного более темным цветом и
изображенного на фрагменте. Действительно,
f11=f22=f/![]() ,
поэтому р22=р11.
Рассматривая равновесие элементарных
объемов в различных точках жидкости,
получим условие:
,
поэтому р22=р11.
Рассматривая равновесие элементарных
объемов в различных точках жидкости,
получим условие:
|
|
(2.2) |
которое и является математическим выражением закона Паскаля. Если этот сосуд соединить при помощи трубки с другим цилиндрическим сосудом сечением S2, то при открывании крана K внутренние напряжения по жидкости, находящейся в соединительной трубке, в соответствии с законом Паскаля передадутся во второй сосуд (рис. 2.1). На поршень, его закрывающий, жидкость будет давить вверх с силой
|
|
(2.3) |
Если S2>S1, то развиваемое усилие F2>F1. Этот выигрыш в силе используется во многих гидроприводящих устройствах (гидроприводах): в приводе ковша экскаватора, рулей ракет и самолетов. На этом же принципе работает гидравлический пресс, гидравлический домкрат и т.д. В системе СИ за единицу давления принимается Паскаль (Па), при этом 1Па=1Н/1м2. В технике в качестве единицы давления используется техническая атмосфера: 1ат=1кГс/1см2=9,8*104 Па.
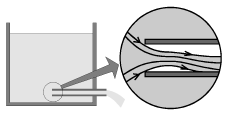
Интересно
отметить, что трубки тока жидкости
расположены преимущественно ближе к
стенке сосуда с отверстием, в то время
как у противоположной (левой на рис.
3.8) стенки жидкость практически
малоподвижна. Это означает, что на левую
стенку действуют силы давления, которое
легко посчитать, используя линейный
закон нарастания гидростатического
давления с глубиной, даваемой формулой
(2.11). Расчет сил давления, действующих
на правую стенку, требует гидродинамического
решения задачи. Однако и без такого
расчета ясно, что в трубке тока, примыкающей
к правой стенке, давление на каждой
глубине будет меньше соответствующего
этой глубине гидростатического давления.
Это означает, что равнодействующая сил
давления, действующих на обе стенки,
направлена в сторону, противоположную
направлению истечения жидкости. Под
действием этой силы, называемой также
реактивной, сосуд, поставленный на
колеса, может придти в движение. Величину
этой силы легко посчитать с использованием
формулы Торичелли. По 3-му закону Ньютона
искомая реактивная сила равна по величине
силе, с которой стенки сосуда действуют
на воду, сообщая ее (по 2-му закону Ньютона)
приращение импульса в направлении
истечения. Поскольку масса, вытекающая
через отверстие с сечением S равна ![]() ,
то изменение импульса в единицу времени
составит величину
,
то изменение импульса в единицу времени
составит величину![]() Поэтому
реактивная сила
Поэтому
реактивная сила
|
|
(3.19) |
|
|
|
Рис. 3.8. |
Отметим, что если бы мы ошибочно приняли, что распределение давлений с глубиной у правой стенки было такое же, как у левой, то реактивная сила получилась бы вдвое меньшей:
|
|
(3.20) |
где ![]() -
величина гидростатического давления
на глубине H, S - площадь отверстия в
правой стенке.
Однако можно добиться
одинакового (гидростатического)
распределения давлений у обеих стенок,
если конец трубки с острой кромкой будет
отстоять от правой стенки, как показано
на рис. 3.9. В этом случае реактивная сила
может определяться с помощью формулы
(3.20). Если же ее вычислять при помощи
(3.19), то в этой формуле надо вместо сечения
трубки S подставить сечение струи воды
в трубке SB=kS,
где коэффициент истечения k
-
величина гидростатического давления
на глубине H, S - площадь отверстия в
правой стенке.
Однако можно добиться
одинакового (гидростатического)
распределения давлений у обеих стенок,
если конец трубки с острой кромкой будет
отстоять от правой стенки, как показано
на рис. 3.9. В этом случае реактивная сила
может определяться с помощью формулы
(3.20). Если же ее вычислять при помощи
(3.19), то в этой формуле надо вместо сечения
трубки S подставить сечение струи воды
в трубке SB=kS,
где коэффициент истечения k![]() 1/2.
При таком истечении трубка будет
заполнена жидкостью приблизительно
наполовину.
1/2.
При таком истечении трубка будет
заполнена жидкостью приблизительно
наполовину.
|
|
|
Рис. 3.9. |
Реактивную силу можно увеличить, если прежде всего повысить скорость истечения жидкости. Для этого следует использовать замкнутый сосуд с отверстием, при этом над свободной поверхностью жидкости создается давление p1>p0. Тогда скорость истечения жидкости из уравнения Бернулли получается равной:
|
|
(3.21) |
а
реактивная сила возрастает линейно с
повышением избыточного давления ![]() над
свободной поверхностью жидкости
над
свободной поверхностью жидкости
.
Плавание тел. Закон Архимеда.
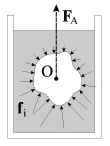
Из повседневной практики известно, что на тела, погруженные в жидкость, действует выталкивающая сила, направленная вертикально вверх. Эта сила является результатом действия сил давления fi= -pni рис. (2.8) и равна
|
|
(2.20) |
Здесь ![]() -
площадь элемента поверхности
тела,ni единичный
вектор, перпендикулярный поверхности,
суммирование производится по всем
элементам поверхности.
-
площадь элемента поверхности
тела,ni единичный
вектор, перпендикулярный поверхности,
суммирование производится по всем
элементам поверхности.
|
|
|
Рис. 2.8. |
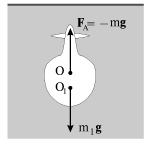
Выталкивающая сила FA , называемая силой Архимеда, может быть подсчитана при учете распределения давления по глубине (2.11) и оказывается равной весу вытесненной жидкости. Предоставляя читателю сделать такой подсчет самостоятельно, вычислим ее, исходя из более простых соображений. Извлечем из сосуда тело и дольем ту же жидкость, восстановив ее прежний уровень (рис. 2.9). Если затем мысленно выделить часть жидкости, замещающую извлеченное тело, то на нее действуют те же силы давления, что и на погруженное тело (см. формулу 2.20). Их сумма FА не только уравновешивает силу тяжести (FA=-mg, m - масса вытесненной жидкости), но и имеет равнодействующую, приложенную к центру масс вытесненной жидкости, или к центру объема O. Центр масс погруженного тела O1 может не совпадать с центром объема O. Это несовпадение имеет большое значение для устойчивого плавания тел, погруженных в жидкость (в кораблестроении используется термин остойчивость). На рис. 2.10 схематично изображено поперечное сечение батискафа, погруженного в воду, при этом его центр тяжести, к которому приложена сила тяжести m1g (m1 - масса батискафа), находится ниже точки приложения Архимедовой силы. Естественно, что при боковом наклоне батискафа момент указанной пары сил будет возвращать его в вертикальное положение.
|
|
|
Рис. 2.9. |
|
|
|
Рис. 2.10. |
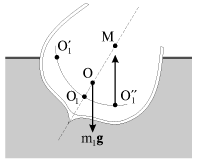
Для тел, плавающих на поверхности жидкости, центр их тяжести всегда будет расположен выше центра объема, погруженного в жидкость, и остойчивость плавания (корабля, например) достигается выбором подобающей формы корабля и его загрузки. Хорошо известно, что карандаш никогда не плавает на поверхности жидкости в вертикальном положении. Пара сил, возникающая при неизбежном случайном отклонении карандаша от вертикали, немедленно "укладывает" его на поверхность (рис. 2.11а). Устойчиво будет плавать "горизонтальный карандаш". При его малейшем наклоне (ситуация б) он будет возвращаться в исходное горизонтальное положение. В судостроении форму судна с учетом его загрузки рассчитывают таким образом, чтобы метацентр М находился выше центра масс судна в т. О. Этот метацентр является центром кривизны кривой O1''O1O1', проходящей через центры объемов погруженных частей корпуса корабля, сменяющих друг друга при его боковой качке (рис. 2.12). Из рисунка видно, что метацентр находится на пересечении плоскости симметрии судна с линией действия Архимедовой силы. При строительстве судов добиваются того, чтобы расстояние OM в несколько раз превышало расстояние OO1.
|
|
|
Рис. 2.11. |
|
|
|
Рис. 2.12. |
Рассмотрение
гидростатики несжимаемой жидкости было
бы не полным, если бы мы не коснулись
вопроса о силах давления, действующих
на дно и стенки сосуда с жидкостью.
Удобно это сделать, обратившись
непосредственно к примерам.
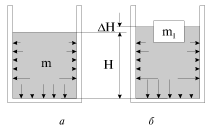
Пример
1. Если
в цилиндрический сосуд с площадью
основания S налита вода, масса которой
m, до уровня H (рис. 2.13а), то давление
жидкости на дно сосуда (без учета силы
атмосферного давления) приведет к
возникновению силы ![]() ,
равной весу налитой жидкости. Если на
поверхность жидкости опустить плавающее
тело массы m1 ,
то давление на дно жидкости увеличится
на величину
,
равной весу налитой жидкости. Если на
поверхность жидкости опустить плавающее
тело массы m1 ,
то давление на дно жидкости увеличится
на величину ![]() ,
где
,
где![]() -
высота подъема уровня жидкости (рис.
2.13б). Дополнительная сила, приложенная
ко дну,
-
высота подъема уровня жидкости (рис.
2.13б). Дополнительная сила, приложенная
ко дну,![]() .
Поскольку объем цилиндрического
слоя
.
Поскольку объем цилиндрического
слоя![]() равен
объему погруженной части тела, то
величина
равен
объему погруженной части тела, то
величина![]() равна
силе Архимеда и, естественно,
равна
силе Архимеда и, естественно,![]() .
Показания весов, на которые поставлен
сосуд с водой, при помещении в него
плавающего тела возрастут на эту
величину.
.
Показания весов, на которые поставлен
сосуд с водой, при помещении в него
плавающего тела возрастут на эту
величину.
|
|
|
Рис. 2.13. |
Пример
2. Если
два легких конических сосуда одинаковой
высоты наполнить водой и расположить
их так, как показано на рис. 2.14 , то в
ситуации (а) сила давления на дно сосуда
с площадью сечения S2 будет
больше веса жидкости:![]() .
В ситуации (б), наоборот,
.
В ситуации (б), наоборот,![]() .
Между тем, при взвешивании сосудов весы
покажут одинаковый результат. На первый
взгляд, мы столкнулись с парадоксом.
Парадокс, однако, разрешается просто,
если мы примем во внимание, что весы
измеряют силу давления сосуда на чашку
весов, равную той силе, с которой жидкость
действует на весь сосуд, включая действие
на его наклонные боковые стенки. В обеих
ситуациях сумма всех этих элементарных
сил одинакова и равна весу жидкости mg.
.
Между тем, при взвешивании сосудов весы
покажут одинаковый результат. На первый
взгляд, мы столкнулись с парадоксом.
Парадокс, однако, разрешается просто,
если мы примем во внимание, что весы
измеряют силу давления сосуда на чашку
весов, равную той силе, с которой жидкость
действует на весь сосуд, включая действие
на его наклонные боковые стенки. В обеих
ситуациях сумма всех этих элементарных
сил одинакова и равна весу жидкости mg.
|
|
|
Рис. 2.14. |
Уравнение неразрывности для сжимаемой жидкости
При
течении газов, особенно при больших
скоростях, их плотность может заметно,
а то и значительно, меняться во времени
и в пространстве. Ясно, что объем втекающей
жидкости может не быть равным объему
вытекающей жидкости через поверхность
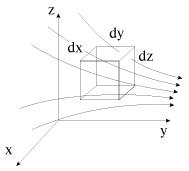
кубика, изображенного на рис. 3.11. Если
такого равенства нет, то масса газа
внутри кубика (а с ней и плотность) будут
со временем меняться. Уравнение (3.24) в
этом случае становится несправедливым.
Однако и здесь можно записать уравнение
неразрывности, основная идея вывода
которого базируется на балансе массы
газа, составляющего физическую суть
равенства (3.1). Поток массы газа через
площадку dSбудет
равен ![]() .
Тогда полный поток массы газа через
боковую поверхность элемента объема
dxdydz, аналогично (3.27), равен
.
Тогда полный поток массы газа через
боковую поверхность элемента объема
dxdydz, аналогично (3.27), равен
|
|
(3.32) |
где
- ![]() новое
векторное поле. Если этот поток
положительный, то масса внутри
элемента
новое
векторное поле. Если этот поток
положительный, то масса внутри
элемента![]() будет
убывать за счет уменьшения во времени
плотности . Поэтому, записывая условие
баланса массы в виде
будет
убывать за счет уменьшения во времени
плотности . Поэтому, записывая условие
баланса массы в виде
|
|
(3.33) |
мы получаем (после сокращения на dxdydz) одно из фундаментальных уравнений гидродинамики - уравнение неразрывности сжимаемой жидкости:
|
|
(3.34) |
Следует
отметить, что при ![]() =const
это уравнение переходит в (3.24).
=const
это уравнение переходит в (3.24).
|
|
|
Рис. 3.11. |
В
электродинамике это уравнение является
также фундаментальным. В самом деле,
если речь идет о движущихся зарядах,
объемная плотность которых равна ![]() ,
то уравнение (3.34) является математическим
выражением универсального закона
сохранения заряда.
,
то уравнение (3.34) является математическим
выражением универсального закона
сохранения заряда.
Уравнения Эйлера и уравнение Бернулли для сжимаемой жидкости.
Динамика сжимаемой жидкости базируется также на 2-м законе Ньютона, записанном для единицы массы жидкости. Равнодействующая сил давления и внешних сил создает ускорение единицы массы, поэтому
|
|
(3.35) |
где
F - внешняя сила, действующая на единицу
массы. Для определения 5-ти неизвестных
величин (vx,
vy,
vz,
p и ![]() )
необходимо дополнить (3.35) материальным
уравнением, связывающим плотность и
давление:
)
необходимо дополнить (3.35) материальным
уравнением, связывающим плотность и
давление:
|
|
(3.36) |
Система
(3.34) - (3.36) носит название уравнений Эйлера
для сжимаемой жидкости. Огромное
количество задач газодинамики решается
на основе анализа этих уравнений.
Воспользуемся
уравнением (3.35) и получим уравнение
Бернулли. Для этого видоизменим правую
часть (3.35), введя вспомогательную
функцию ![]() (2.27),
и учтем (2.29). Тогда (3.35) примет вид
(2.27),
и учтем (2.29). Тогда (3.35) примет вид
|
|
(3.37) |
При
стационарном течении ![]() .
В направлении оси трубки тока (вдоль
криволинейной координаты
.
В направлении оси трубки тока (вдоль
криволинейной координаты![]() )
можно записать
)
можно записать
|
|
(3.38) |
Поскольку
потенциальная энергия единицы массы ![]() ,
а
,
а![]() ,
то, по аналогии с (3.13), перепишем (3.38) в
виде:
,
то, по аналогии с (3.13), перепишем (3.38) в
виде:
|
|
(3.39) |
Интегрируя (3.39) вдоль трубки тока, получаем уравнение Бернулли для сжимаемой жидкости
|
|
(3.40) |
Здесь
h - положение по вертикали сечения трубки
тока с координатой ![]() .
Очевидно, что
.
Очевидно, что![]() .
Постоянная в (3.40) определяется заданием
скорости v1 и
высоты h1 в
фиксированном сечении с координатой
.
Постоянная в (3.40) определяется заданием
скорости v1 и
высоты h1 в
фиксированном сечении с координатой ![]() .
С учетом этого, уравнение (3.40) обретает
вид
.
С учетом этого, уравнение (3.40) обретает
вид
|
|
(3.41) |
Для
практического использования уравнения
Бернулли необходимо знание материальной
связи между p и ![]() .
Для случая несжимаемой жидкости (
.
Для случая несжимаемой жидкости (![]() =
const) уравнение (3.41) переходит в (3.15).
Если
речь идет о потоке газа, то при его
быстром сжатии (увеличение плотности)
газ будет нагреваться. Из-за плохой
теплопроводности газа тепло не будет
успевать уходить из нагретых областей.
Поэтому для установления материальной
связи
=
const) уравнение (3.41) переходит в (3.15).
Если
речь идет о потоке газа, то при его
быстром сжатии (увеличение плотности)
газ будет нагреваться. Из-за плохой
теплопроводности газа тепло не будет
успевать уходить из нагретых областей.
Поэтому для установления материальной
связи![]() воспользуемся
адиабатическим приближением:
воспользуемся
адиабатическим приближением:
|
|
(3.42) |
где
показатель адиабаты ![]() .
Такая связь получается из первого начала
термодинамики и уравнения состояния
идеального газа (2.32) при условии отсутствия
теплообмена между нагретой областью и
окружающей средой. Давление в (3.42)
возрастает с плотностью быстрее, чем
при изотермическом процессе, так как
.
Такая связь получается из первого начала
термодинамики и уравнения состояния
идеального газа (2.32) при условии отсутствия
теплообмена между нагретой областью и
окружающей средой. Давление в (3.42)
возрастает с плотностью быстрее, чем
при изотермическом процессе, так как![]() .
В курсе молекулярной физики будет
показано. что
.
В курсе молекулярной физики будет
показано. что![]() (Cp и
CV -
теплоемкости при постоянных давлении
и объеме соответственно). Для воздуха,
состоящего главным образом из двухатомных
газов,
(Cp и
CV -
теплоемкости при постоянных давлении
и объеме соответственно). Для воздуха,
состоящего главным образом из двухатомных
газов, ![]() =
1,4.
Если подставить (3.42) в (3.41) и выполнить
простейшее интегрирование, то можно
записать выражение для распределения
давления вдоль трубки тока:
=
1,4.
Если подставить (3.42) в (3.41) и выполнить
простейшее интегрирование, то можно
записать выражение для распределения
давления вдоль трубки тока:
|
|
(3.43) |
Не умаляя общности, будем считать трубку тока горизонтальной (h=h1). Положим далее скорости течения такими, что
|
|
(3.44) |
где ![]() -
параметр, имеющий размерность скорости.
Как мы увидим несколько позднее, скорость
звука в газе
-
параметр, имеющий размерность скорости.
Как мы увидим несколько позднее, скорость
звука в газе
|
|
(3.45) |
При нормальных условиях для атмосферы с=336 м/с. В этом случае (3.43) можно разложить в ряд:
|
|
(3.46) |
Если
пренебречь квадратичным членом в (3.46),
то распределение давлений соответствует
течению несжимаемой жидкости с
плотностью ![]() =const.
Квадратичный член начинает давать вклад
в распределение давлений при скоростях
потока, соизмеримых со скоростью звука
с1.
Подставив
(3.42) в (3.43), получаем распределение
плотности вдоль трубки тока:
=const.
Квадратичный член начинает давать вклад
в распределение давлений при скоростях
потока, соизмеримых со скоростью звука
с1.
Подставив
(3.42) в (3.43), получаем распределение
плотности вдоль трубки тока:
|
|
(3.47) |
Для горизонтальной трубки тока и при условии (3.44) распределение плотности (3.47) имеет вид:
|
|
(3.48) |
Таким
образом, изменение плотности газа
необходимо принимать в учет только при
скоростях течения, сопоставимых по
порядку величины со скоростью звука,
определяемой, как следует из (3.45),
давлением и плотностью в этом потоке.
Если
же скорость течения ![]() ,
то сжимаемостью газа можно пренебречь
и оперировать с ним, как и с жидкостью.
,
то сжимаемостью газа можно пренебречь
и оперировать с ним, как и с жидкостью.
Сплошные тела. Абсолютно упругое тело. Виды деформаций.
До сих пор рассматривалась механика недеформируемого твердого тела. Что такое деформация?
Деформация – процесс силового воздействия, в результате которого изменяется форма тел под действием приложенных к ним внешних сил.
Известно, что все тела состоят из молекул и атомов, между которыми существуют силы взаимодействия, поэтому и формируемое тело можно рассматривать как систему материальных точек, расстояния между которыми изменяются при их деформации.
Но во многих случаях более целесообразно рассматривать деформируемое тело, как сплошное. Так обычно поступают при всех инженерных расчетах (например: прогиб балки, кручение осей и др.) Поэтому в дальнейшем все виды деформаций мы будем рассматривать с макроскопической точки зрения, а тела представлять как сплошные.
Твердые тела сопротивляются как изменению объема, так и формы, т.е. любому деформированию. Действие силы оказывает на тело давление.
Давления, возникающие в твердом теле при его деформировании, называются упругими напряжениями.
Сила упругих напряжений в твердом теле может иметь любое направление по отношению к площадке, на которую она давит.
Все деформации делятся на виды:
а)
|
|
Деформации |
| |||
|
|
|
| |||
|
Однородная |
|
Неоднородная | |||
|
|
|
| |||
|
Деформация, при которой все точки тела, лежащие на одной вертикали, не смещаются с нее, а расстояния между слоями остаются во всех точках одинаковыми (растяжение, сжатие) |
|
(изгиб, кручение) | |||
|
|
|
|
|
| |
б)
|
|
Деформации |
| ||||
|
|
|
| ||||
|
Упругая |
|
Неупругая (пластичная) | ||||
|
Когда после снятия нагрузки форма тела восстанавливается (деформация исчезает) |
|
| ||||
|
|
|
|
|
| ||
Тела, в которых после прекращения действия внешней силы деформация полностью исчезает и восстанавливается первоначальная форма тела, называются абсолютно упругими телами.
Тела, не восстанавливающие свою первоначальную форму после снятия действия сил, называются неупругими (пластичными).
В природе нет абсолютно упругих и абсолютно неупругих тел. При изменении условий (температуры, нагрузки) упругое тело может перейти в состояние пластичное и наоборот.
|
Пример: |
Резина: |
Пластичная при нормальных температурах |
|
Упругая при низких температурах |
Построение теории процессов деформации – задача молекулярной и атомной физики.
Примерное объяснение деформации может быть дано следующее: между атомами и молекулами внутри твердого тела существуют силы притяжения и отталкивания, обеспечивающие их взаимодействие друг с другом и удерживающие их друг около друга. Внешние силы смещают атомы со своих мест. Если сдвиг внешней силы невелик, то после прекращения внешнего действия частицы вернутся к прежнему взаимному положению, это упругая деформация. Если атомы меняют соседей и взаимодействуют с другими элементами решетки (структуры) после прекращения воздействия, то это пластичная деформация.