Линейная множественная модель
Включение в регрессионную модель новых переменных усложняет получаемые формулы и вычисления. Это приводит к целесообразности матричных обозначений. Матричное описание регрессии облегчает как теоретический анализ, так и необходимые расчетные процедуры.
Предположим, что функциональная структура ящика снова имеет линейную зависимость, но количество входных сигналов, действующих одновременно на объект, равно m (см. рис. 2.7):
.
(2.8)
Рис. 2.7. Обозначение многомерного черного ящика на схемах
Исходными
данными при оценке параметров
является прямоугольная матрица входов
Х
и вектор результатов
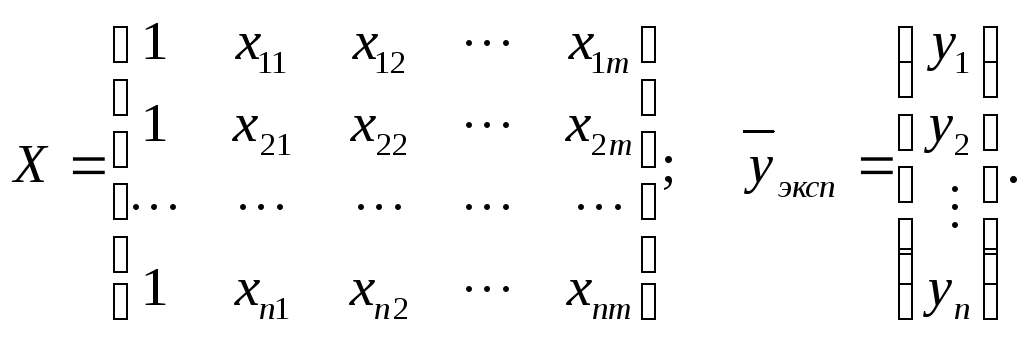(2.9)
Строки
матрицы Х
соответствуют результатам регистрации
всех наблюдаемых параметров объекта в
одном эксперименте, а столбцы содержат
результаты наблюдений за одним параметром
(фактором) во всех экспериментах. Первый
столбец матрицы Х,
состоящий из единиц, соответствует
коэффициенту модели
.
Уравнение регрессии (2.8) в матричной форме для данных (2.9) имеет вид
,
где
- вектор-столбец параметров модели.
Применяя
метод наименьших квадратов, нужно найти
минимум суммы
.
(2.10)
Учитывая,
что при транспонировании произведения
матриц получается произведение матриц,
взятых в обратном порядке, т.е.
после раскрытия скобок получим:
.
(2.11)
Произведение
есть матрица размера
,
т.е. величина скалярная, следовательно, оно не меняется при транспонировании, т.е.
.
Поэтому условие минимизации (2.11) примет вид:
.
(2.12)
На
основании необходимого условия экстремума
функции нескольких переменных
необходимо приравнять нулю частные
производные по этим переменным или в
матричной форме – вектор частных
производных
.
Для вектора частных производных в курсе высшей математики доказаны следующие формулы:
,
где a и c – вектор-столбцы; A – симметричная матрица.
.
Полагая
,
а матрицу
(она является симметричной), найдем:
,
откуда
получаем систему нормальных уравнений
в матричной форме для определения
вектора
:
.
(2.13)
Раскроем последнее выражение
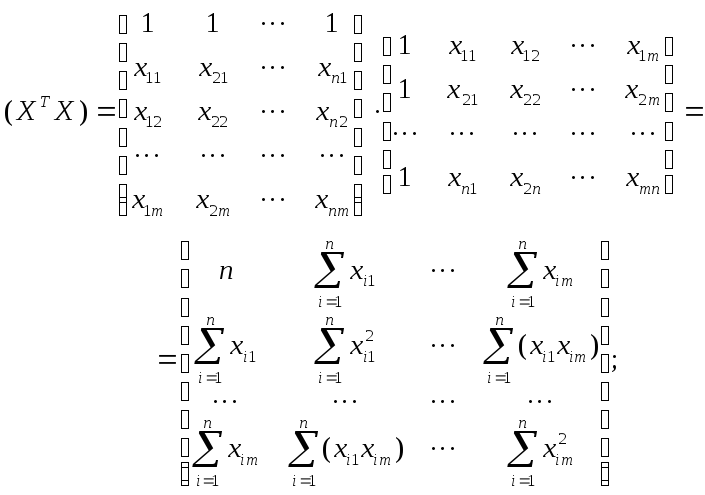(2.14)
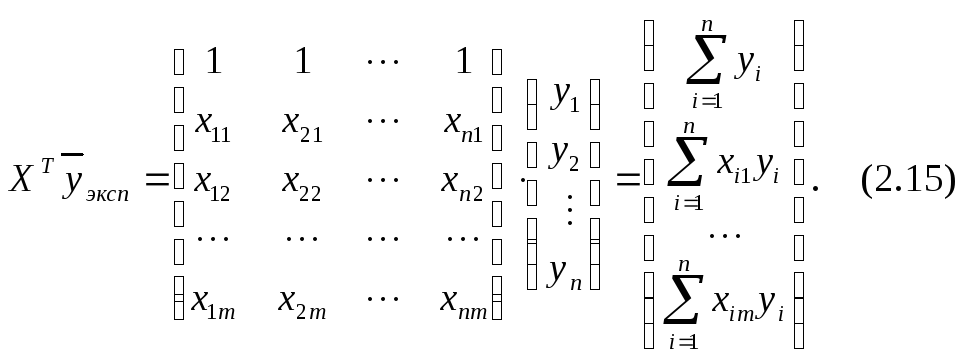
В частном случае из рассматриваемого матричного уравнения (2.13) с учетом (2.14) и (2.15) для одной переменной (m=1) нетрудно получить уже рассмотренную систему нормальных уравнений (2.7). Действительно, в этом случае матричное уравнение (2.13) принимает вид:
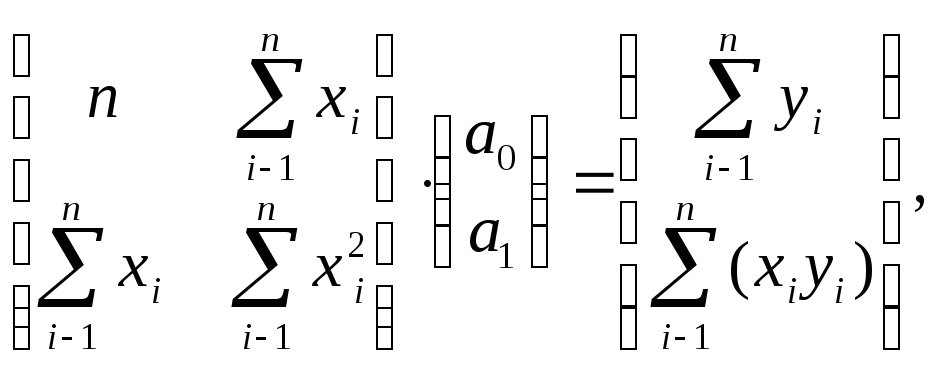
откуда непосредственно следует система нормальных уравнений для парной линейной регрессии.
Умножая
слева обе части уравнения (2.13) на обратную
матрицу
определим искомые коэффициенты уравнения
регрессии (2.8)
.
Если уравнение регрессии задано в виде полинома степени p
то матрица X называется матрицей Вандермонда и имеет следующую структуру
.
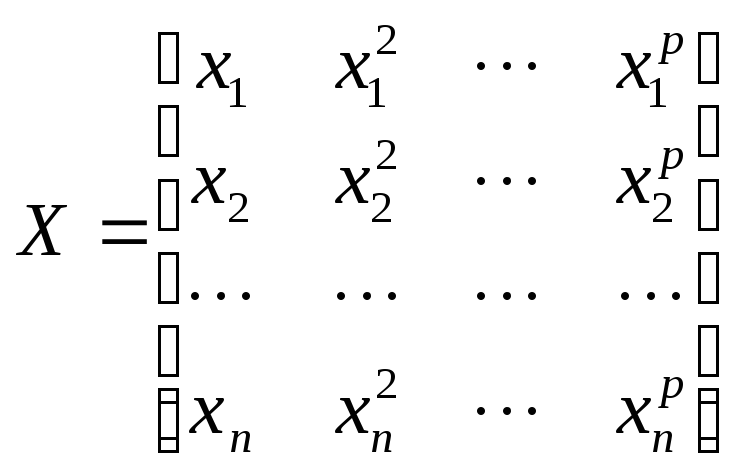Нелинейные регрессионные модели
В данном разделе покажем, как нелинейная регрессионная модель может быть сведена к исследованию линейной множественной модели.
А) Полиномиальная множественная регрессионная модель
Если черный ящик имеет, например, два входа, а зависимость выхода от входов напоминает квадратичную, то целесообразно выбрать такую гипотезу:
.
Обозначим:
и
подставим эти выражения в предыдущую
формулу:
.
Таким образом, данная задача сведена к линейной множественной модели. А модель черного ящика теперь выглядит так, как показано на рис. 2.8.
Рис. 2.8. Преобразованная модель черного ящика
Далее
используется метод наименьших квадратов.
Как и раньше: строится система нормальных
уравнений, и определяются значения
.