
лекции по эконометрике
.pdfФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ
ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ ДОНСКОЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
А.И. Полисмаков
ЛЕКЦИИ ПО ЭКОНОМЕТРИКЕ
Ростов-на-Дону 2009
УДК 330.43(075.8) ББК 65 в6 873 П 50
Рецензент канд. техн. наук, доцент О.А.Игнатова
П 50 Полисмаков А.И. Лекции по эконометрике / А.И. Полисмаков - Ростов н/Д: Издательский центр ДГТУ, 2009. – 78 с.
Лекции представляют тексты для краткого курса эконометрики, предусмотренного Госстандартом для студентов III курса специальности «Мировая экономика». Учебный материал сопровождается примерами, задачами и контрольными вопросами. Может быть использовано в качестве введения в круг проблем технического анализа.
УДК 330.43(075.8) ББК 65 в6 873
Печатается по решению редакционно-издательского совета Донского государственного технического университета
Научный редактор канд. эконом. наук Н.В. Бурьянова
Полисмаков А.И., 2009
Издательский центр ДГТУ, 2009

Полисмаков Александр Иванович
ЛЕКЦИИ ПО ЭКОНОМЕТРИКЕ
Учебное пособие
Редактор О.А.Водолазова Компьютерная обработка И.В.Кикичева
Тем план 2009, поз.51
____________________________________________________________ В печать 21.04.09. Объём 4,9 усл. п. л. Офсет. Формат 60х84/64.
Бумага тип №3. Заказ №181. Тираж 150 экз. Цена свободная
Издательский центр ДГТУ Адрес университета и полиграфического предприятия:
344000, г. Ростов-на-Дону, пл. Гагарина,1.

Лекция 1. ЦЕЛЬ И СОДЕРЖАНИЕ ЭКОНОМЕТРИКИ
1.1. Введение
Современный человек (в отличие от своего доисторического предка) получает большое количество необходимой ему информации в численном виде. Например, из различных источников мы ежедневно узнаем: температуру окружающего воздуха (в 0С); влажность (в %-х); давление (в мм. ртутного столба); цены на основные продукты питания – хлеб, молоко, колбасу и пр. (в действующих денежных единицах); обменные курсы валют (курсы доллара, евро); предлагаемый размер оплаты своего труда; предполагаемые расходы по оплате необходимых услуг и т.д. Количество численной информации значительно увеличивается, если человек в своей профессиональной деятельности связан с экономикой, бизнесом и другими численно-емкими видами деятельности. При этом крайне важно не только получать необходимую информацию, но и иметь возможность для ее оценки, переработки и принятия на ее основе различных решений. Для этого необходимы время, опыт, знания. Например, если данный человек знает, что некоторая переменная величина «х» связана с другой важной для него переменной величиной «у» прямой пропорциональной зависимостью у=ax, где а>0, то информацию об увеличении переменной «х» он воспринимает как положительную для себя информацию, так как переменная величина «у», в увеличении которой он заинтересован, тоже увеличивается.
Эконометрика – это раздел экономики, который занимается разработкой и применением методов математической статистики для измерения и анализа взаимосвязей между экономическими переменными.
Цель эконометрики – это формулирование конкретных (численных) экономических прогнозов на основе уже имеющегося статистического материала. Другими словами, если статистика изучает прошлое, то эконометрика пытается заглянуть в будущее, используя для этого разнообразные математические методы.
Курс эконометрики занимает важное место в программах экономических вузов во всем мире. Эконометрические методы необходимы и ученым, и практикам, так как от их правильного применения зависит успех в банковском деле, финансах, бизнесе и т.д. Поэтому научные исследования в этом направлении развиваются достаточно интенсивно, особенно в последнем десятилетии. Не случайно единственная Нобелевская премия в области экономики в 2004 году была присуждена за работы в области эконометрического анализа.
1.2. Ковариация. Корреляция
(необходимые сведения из курса математической статистики)
Известно, что мерой взаимосвязи между двумя переменными является корреляционный момент. Выборочной ковариацией между двумя переменными (факторами) х и у называется величина:
|
|
|
|
|
|
|
1 |
|
n |
(xi |
|
|
) yi |
|
|
|
, |
|
||||||
|
|
|
|
cov (x,y) = |
i 1 |
х |
y |
(1) |
||||||||||||||||
n |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
1 |
|
n |
|
|
|
|
|
|
1 |
n |
|
|
|
|
|
|
где |
x |
, |
y |
- выборочные средние: |
x |
|
|
xi , |
|
y |
|
yi |
; |
|
|
(xi ,yi ) – пара соответствующих |
||||||||
n |
|
n |
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
i 1 |
|
|
|
|
|
|
i 1 |
|
|
|
|
|
||||
значений переменных величин х и у.
Рассмотрим для примера динамику изменения расходов населения США на бензин (у) в млрд. долларов и реальных цен на него (х) в % за период с 1973 по 1982 годы (табл.1)

Таблица 1
Динамика изменения расходов населения США на бензин за период с 1973 по 1982 годы (цена в 1972 году принята за 100%)
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Годы |
i |
y i |
x i |
xi x |
|
y i y |
|
(xi x) (yi |
y) |
xi yi |
( xi x)2 |
(yi |
y |
)2 |
|
|
|
||||||||||||||||||
|
|
|
|
|
|
1973 |
|
|
1 |
|
|
- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
26,2 |
103,5 |
39,86 |
-0.07 |
|
|
2.79 |
|
|
|
|
|
2711.7 |
1588.82 |
0.01 |
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
1974 |
|
|
2 |
|
|
- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
24,8 |
127 |
16.36 |
-1.47 |
|
|
24.05 |
|
|
|
|
|
3149.6 |
267.65 |
2.16 |
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
1975 |
|
|
3 |
|
|
- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
25,6 |
126 |
17.36 |
-0.67 |
|
|
11.63 |
|
|
|
|
|
3225.6 |
301.37 |
0.45 |
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
1976 |
|
|
4 |
|
|
- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
26,8 |
124,8 |
18.56 |
0.53 |
|
|
-9.84 |
|
|
|
|
|
3344.64 |
344.47 |
0.28 |
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
1977 |
|
|
5 |
27,7 |
124,7 |
- |
|
|
1.43 |
|
|
-26.68 |
|
|
|
|
|
3454.19 |
348.20 |
2.05 |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
18.66 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
1978 |
|
|
6 |
|
|
- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
28,3 |
121,6 |
21.76 |
2.03 |
|
|
-44.17 |
|
|
|
|
|
3441.28 |
473.50 |
4.12 |
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
1979 |
|
|
7 |
27,4 |
149,7 |
6.34 |
|
1.13 |
|
|
7.16 |
|
|
|
|
|
4101.78 |
40.20 |
1.28 |
|
|
|
|
||||||||||||
|
|
|
|
|
|
1980 |
|
|
8 |
25,1 |
188,8 |
45.44 |
-1.17 |
|
|
-53.16 |
|
|
|
|
|
4738.88 |
2064.79 |
1.37 |
|
|
|
|
|||||||||||||
|
|
|
|
|
|
1981 |
|
|
9 |
25,2 |
193,6 |
50.24 |
-1.67 |
|
|
-53.76 |
|
|
|
|
|
4878.72 |
2524.06 |
1.15 |
|
|
|
|
|||||||||||||
|
|
|
|
|
|
1982 |
|
|
10 |
25,6 |
173,9 |
30.54 |
-0.67 |
|
|
-20.46 |
|
|
|
|
|
4451.84 |
932.69 |
0.45 |
|
|
|
|
|||||||||||||
|
|
|
|
|
|
Итого: |
|
262,7 |
1433,6 |
|
|
|
|
|
|
|
|
-162,6 |
|
|
|
|
|
|
8885,8 |
13,3 |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
26,3 |
|
|
|
|
143,4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
Задача 1. |
По данным табл.1 вычислить выборочную ковариацию |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
26,3; |
|
|
143,4. Далее найдем разности yi |
|
|
||||||||||||||||||||||||
|
|
|
Решение. Найдем выборочные средние: |
|
y |
|
x |
y |
|||||||||||||||||||||||||||||||||
и хi |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
x |
и занесем результаты в расчетную таблицу. Найдем произведение полученных разностей, |
||||||||||||||||||||||||||||||||||||||||
т.е. (xi |
|
x |
)(yi |
y |
) |
для всех значений I, начиная с i 1 до i 10. |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
По формуле (1) найдем среднее значение этих произведений, т.е. выборочную кова- |
|||||||||||||||||||||||||||||||||||
риацию: cov(x,y) 16,24.
Заметим, что полученное значение ковариации между yi и xi отрицательно. Это говорит о
том, что между этими величинами существует некоторая отрицательная связь. То есть увеличение одной переменной приводит к уменьшению второй и наоборот. Однако величина выборочной ковариации не позволяет судить о степени взаимозависимости переменных. Дело в том, что ковариация зависит от единиц, в которых измеряются переменные. Например, если бы в рассмотренном выше примере расходы населения США на бензин были представлены не в миллиардах, а в миллионах долларов, то мы бы получили другое значение коэффициента ковариации.
Кроме формулы (1), существует другая, эквивалентная ей формула для вычисления ковариа-
ции:
|
1 |
n |
|
|||||
cov(x,y) ( |
xi yi ) |
|
|
|
. |
|
||
x |
y |
(2) |
||||||
n |
||||||||
|
i 1 |
|
||||||
Из курса математической статистики известно, что многие выборочные характеристики, такие как выборочная дисперсия, выборочная ковариация и др. имеют отрицательное смещение, то есть при выборках небольшого объема (при малых «n») обычные формулы для их вычисления дают зани-
женные значения. Этот недостаток легко устраняется введением поправочного коэффициента n . n 1
Поэтому более точные, не смещенные оценки этих выборочных характеристик, можно найти по формулам:
выборочная дисперсия:
Var(x) |
1 |
|
|
n |
(xi |
|
|
)2 |
|
|||||
|
|
x |
(3) |
|||||||||||
n 1 |
i 1 |
|||||||||||||
|
|
|
|
|
|
|
|
|
||||||
или |
|
|
|
|
|
|
|
|
|
|
||||
1 |
|
|
n |
|
2 |
|
|
2 |
|
|||||
|
|
|
|
|
||||||||||
Var(x) ( |
|
i 1 |
xi |
) x ; |
(4) |
|||||||||
n 1 |
||||||||||||||
выборочная ковариация:

1 |
|
n |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|||||
cov(x,y) |
|
|
|
(xi x)(yi |
y) |
(5) |
|||||||
n 1 |
|||||||||||||
|
i 1 |
|
|
|
|
|
|
|
|
||||
или |
|
|
|
|
|
|
|
|
|
||||
1 |
|
n |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|||||
cov(x;y) ( |
|
i 1 |
xi yi ) xy. |
(6) |
|||||||||
n 1 |
|||||||||||||
Формулами (3)-(6) мы и будем пользоваться далее.
Более точной (по сравнению с выборочной ковариацией) мерой степени зависимости между переменными является коэффициент корреляции.
Выборочный коэффициент корреляции определяется по формуле:
r |
|
|
cov(x,y) |
|
|
cov(x,y) |
, |
(7) |
||
|
|
|
|
|||||||
|
|
|||||||||
x,y |
|
Var(x)Var(y) |
|
|
|
x |
y |
|
||
где x и y - выборочные средние квадратические отклонения факторов х и у.
Можно доказать, что если переменные х и у независимы, то cov(x,y) 0. Отсюда следует,
что в этом случае и коэффициент корреляции тоже равен 0. Если существует строгая положительная линейная зависимость между х и у, то коэффициент корреляции принимает максимальное значение, равное 1. При строгой отрицательной линейной зависимости коэффициент корреляции равен своему минимальному значению 1.
Замечание. Формула (7) дает не смещенную оценку выборочного коэффициента корреляции rx,y . Однако, следует помнить, что за счет случайных факторов при вычислении коэффициента кор-
реляции по выборке небольшого объема полученная с помощью формулы (7) оценка rx,y может не-
сколько отличаться от теоретического значения коэффициента корреляции.
Обозначим теоретический коэффициент корреляции ρ x,y . Важно понимать, что если выбо-
рочный коэффициент rx,y 0, то это необязательно означает, что ρ x,y 0 и что связь между пере-
менными отсутствует.
Заметим, что при вычислении коэффициента корреляции необязательно вводить поправоч-
ный коэффициент n в формулы для вычисления ковариации и дисперсии, так как в формуле (7) n 1
эти коэффициенты все равно сокращаются.
Задача 2. По данным табл.1 вычислить коэффициент корреляции rx,y .
Решение. По данным последних двух столбцов (см. табл.1) вычислим Var(x) и Var(y) по формулам:
|
1 |
n |
|
|
|
|
|
|
|
|
1 |
n |
|
|
|
|
Var(x) |
(xi |
|
|
)2; |
Var(y) |
(yi |
|
|
)2 . (8) |
|||||||
x |
y |
|||||||||||||||
n |
n |
|||||||||||||||
|
i 1 |
|
|
|
|
|
|
|
|
i 1 |
|
|
|
|||
Получим: Var(x) 888,58; |
Var(y) 1,33; |
|
|
|
|
|
|
|||||||||
|
|
|
r |
|
|
|
16,24 |
0,47 . |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
x,y |
|
|
|
888,58 1,33 |
|
|
|
|
|
|
|||
Вывод: между ценой на бензин (х) и расходами населения США на его приобретение (у) имеется слабая отрицательная связь. То есть при увеличении цены (х) происходит, в среднем, снижение совокупных расходов на бензин.
Вопросы к теме:
1.Приведите примеры экономических показателей. Для решения каких экономических задач они нужны?
2.Сформулируйте основную задачу эконометрики.
3.В чем состоит главное отличие основной задачи эконометрики от задач статистики?
4.Назовите простейший показатель, указывающий на наличие связи между двумя экономическими переменными (факторами).
5.Напишите формулы, по которым вычисляются:
а) выборочная средняя ( х );
б) выборочная дисперсия (вариация) (Var(x)); в) ковариация между x и у : (cov(x,y));
г) коэффициент парной корреляции между х и у : (rx,y ).
6)Что такое поправочный коэффициент, устраняющий смещение выборочных характеристик,
ичему он равен?
7)В каких случаях использование поправочного коэффициента необязательно?
8)В чем состоит преимущество коэффициента корреляции над коэффициентом ковариации как меры, характеризующей наличие связи между х и у?
9)Какой вывод можно сделать, если cov(x,y)=0 ?
10)Существует ли связь между переменными, если коэффициент корреляции rx,y =1 ?
Лекция 2. ПАРНЫЙ РЕГРЕССИОННЫЙ АНАЛИЗ
2.1. Линейная модель
Если коэффициент корреляции |rx,y|>0, то две переменные x и y связаны друг с другом. Однако точно математическую форму выражения этой связи выявить довольно сложно.
В экономике точная формулировка связи между какими-либо двумя экономическими показателями вряд ли возможна, за исключением тех случаев, когда эта связь существует по определению. Поэтому в статистическом анализе и эконометрике факт неточности формулировки связи между дву-
мя переменными учитывается путём введения так называемого случайного фактора. |
|
Простейшая линейная модель при этом будет иметь вид : |
|
y=ax+b+u, |
(9) |
где y - зависимая (объясняемая) переменная; x - независимая (объясняющая) переменная; a,b - постоянные числовые параметры; u - случайный член (фактор).
Первые два слагаемых: ax+b - образуют неслучайную составляющую этой модели;u- случайную составляющую.
Почему на этапе анализа связи между двумя переменными нужно включать случайный член? Причин несколько:
1.Невключение других объясняющих переменных. Возможно, что на изменение пере-
менной величины y оказывают влияние, кроме x, и другие неучтённые в линейной модели (9) факторы (переменные). К таким факторам могут относиться те, которые мы, ввиду недостаточного понимания сути рассматриваемой связи, не включили в формулу (9).
Некоторые, например, психологические факторы, мы не можем измерить количественно.
2.Агрегирование (объединение) переменных. Например, функция суммарного спроса представляет собой выражение совокупности решений отдельных потребителей о расходах на покупку данного товара. Так как индивидуальные решения, вероятно, имеют разные параметры, то любая попытка объединить эти решения будет приближенной. Поэтому соотношение между совокупными расходами и доходом должно содержать случайный фактор.
3.Неправильная функциональная спецификация зависимости. Функциональное со-
отношение между y и x может быть выбрано математически неправильно. Например, истинная зависимость между y и x может, не являться линейной, а какой-либо иной (степенной, и т.д.). Однако и любая другая математическая формула также будет являться лишь приближением и может давать расхождения с реальными значениями переменных. Эти расхождения также могут быть объяснены наличием в формуле (9) случайного члена.
4.Ошибки измерения значений переменных. Если в измерении хотя бы одной из взаи-
мосвязанных переменных имеются ошибки, то точное выполнение любого функционального соотношения между ними невозможно. В этом случае в это функциональное соотношение необходимо включать случайный член.
Остаточный (случайный) член обычно является суммарным проявлением действия всех этих факторов. Если бы этот член отсутствовал, то мы смогли бы точно вычислить значения параметров функционального соотношения между x и y.
2.2. Предварительный графический анализ статистических данных
Допустим, что у нас имеются статистические данные указывающие значения двух переменных величин x и y, и есть основания предполагать, что эти величины взаимосвязаны. Мы хотим максимально точно определить математическую формулу для выражения этой связи. С чего начать? Разумнее всего с графического анализа. В системе координат (x, y) изобразим все точки, координаты которых заданы имеющимися в нашем распоряжении статистическими данными. В результате также мы получаем графическое представление этих данных. При этом могут встретиться различные виды «картинок» (рис.1):
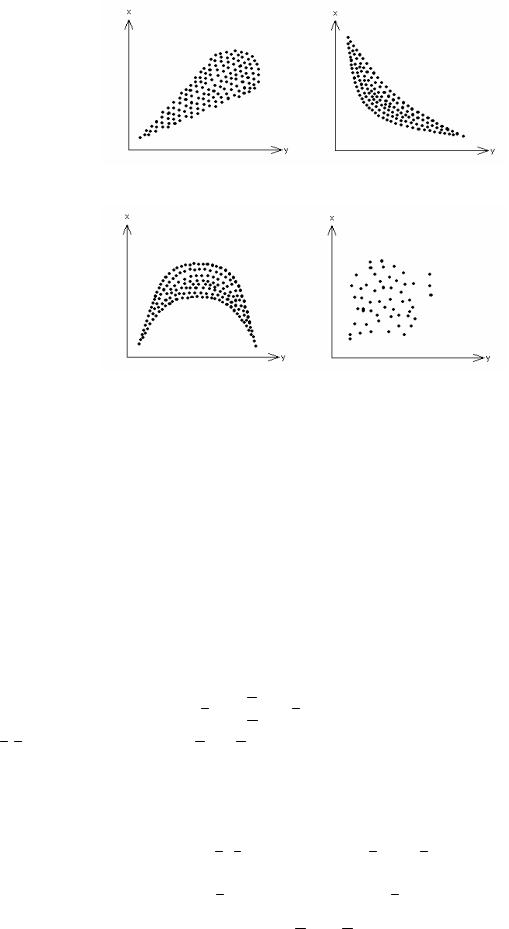
А |
В |
С |
D |
Рис.1. Примеры графического представления статистических данных
Визуальный осмотр графических представлений А, В, С и D приводит к следующим предварительным выводам:
1)зависимость между x и y, представленная на картинке А, скорее всего линейная, с положительной ковариацией и может быть выражена линейной моделью (9);
2)зависимость между x и у в случае B скорее всего нелинейная (возможно степенная?), так как геометрическая форма картинки напоминает “расплывшуюся” гиперболу. Ковариация отрицательная. Линейная модель (9) не годится;
3)зависимость на картинке С точно нелинейная с переменной по знаку ковариацией (возможно парабола?), формула (9) также не подходит;
4)зависимость между x и y на картинке D слабая, возможно линейная с положительной корреляцией. Можно попробовать описать её с помощью модели (9),но удельный вес случайного члена “u” в этой модели будет очень значителен.
Случаи, подобные 2) и 3), когда математическая спецификация модели связи между x и y затруднена, мы рассмотрим позже в лекции, посвященной нелинейной регрессии.
А сейчас перейдем к более детальному рассмотрению случая парной линейной регрессии.
2.3. Уравнение линейной регрессии.
Расчёт параметров по методу наименьших квадратов
Из курса математической статистики известно, что уравнение линейной регрессии между y и x имеет вид:
|
|
|
|
|
y |
y |
r |
|
|
|
|
y |
x |
x |
, |
|
|
|
|
|
|
|
(10) |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
x |
, |
y |
|
|
|
|
|
|
|
xy |
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
где |
- выборочные средние; |
x |
и |
y |
|
- |
выборочные средние квадратические отклонения; rxy - |
||||||||||||||||||||||||||||
|
коэффициент корреляции. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
Уравнение ( 10 ) мы запишем |
далее в виде |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
где |
y = b0 |
+ b1x |
|
+ u , |
|
|
|
|
|
|
|
|
|
|
|
(11) |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|||
|
|
|
|
b |
xi yi |
nx |
|
y |
|
|
|
|
|
b |
xi |
x |
yi |
|
y |
|
|
||||||||||||||
|
|
|
|
i 1 |
|
|
|
|
|
|
|
|
|
|
; |
|
или |
i 1 |
|
|
|
|
, |
(12) |
|||||||||||
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
||||||||||||||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
xi2 n |
x |
2 |
|
|
|
|
|
|
|
|
|
|
xi |
|
x |
2 |
|
|||||||||||||
|
|
|
|
|
i 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i 1 |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b0 |
|
y |
b1 |
x |
. |
|
|
|
|
|
|
|
|
|||||
Вычисленные по формуле (12) значения b0 и b1 представляют собой наилучшие (с точки
зрения метода наименьших квадратов) числовые оценки теоретических значений параметров линейной модели (11). Применение формулы (12) позволяет минимизировать сумму квадратов случайного фактора «u»;
n
minu2 min (yi b0 b1xi )2,
i 1
т.е. минимизировать сумму квадратов отклонений реальных значений переменной уi от вычисленных значений у€i этой переменной с помощью линейной модели (11)
n
(yi y€i )2 min.
i 1
Будет ли линейная модель регрессии в этом случае достаточно надежной, чтобы её можно было использовать для прогнозирования значений переменной у в зависимости от изменения переменной х? Или, другими словами, насколько качественно объясняющая переменная х объясняет изменения переменной у при условии принятия линейной модели регрессии?
Обсуждение данного важного вопроса мы начнем в следующей лекции.
Пример. Анализируя зависимость расходов населения США на продукты питания (у) от дохода (х), американские экономисты получили следующие уравнение регрессии:
y=55,3+0,093x ; (x,y-млрд. долларов).
Это уравнение позволяет предсказать, например, что если совокупный годовой доход населения увеличится на 1 млрд. долларов, то расходы на питание возрастут на 93 млн. долларов. Это позволяет прогнозировать изменение спроса. До настоящего времени это уравнение выполняется достаточно точно, т.е. данная регрессия оказалась достаточно качественной. Однако является ли данная модель наилучшей?
Вопросы к теме:
1.Назовите переменные, входящие в уравнение линейной модели регрессии (y=ax+b+u).
2.Почему на этапе анализа связи между экономическими переменными необходимо включать
вмодель регрессии случайный член?
3.Дайте примерное графическое изображение зависимости между х и у в случае, когда:
а) связь между х и у линейная, положительная; б) связь между х и у линейная, отрицательная; в) связь между х и у отсутствует.
4. Напишите уравнение парной линейной регрессии между х и у, используя известные выборочные средние х и у, средние квадратические отклонения x и y и выборочный коэффициент
парной корреляции rx,y .
5.В чем суть метода наименьших квадратов, применяемого при вычислении неизвестных параметров уравнения парной линейной регрессии?
6.Напишите формулы для вычисления параметров уравнения парной линейной регрессии с помощью метода наименьших квадратов.
7.Как можно использовать графическую интерпретацию данных для обнаружения ошибки, допущенной при вычислении параметров уравнения регрессии?
