Комбинаторные схемы

Размещения с повторениями

Задача 1. Для запирания сейфов и автоматических камер хранения применяют секретные замки, которые открываются лишь тогда, когда набрано некоторое «тайное слово». Это слово набирают с помощью одного или нескольких дисков, на которых нанесены буквы (или цифры). Пусть на диск нанесены 12 букв, а секретное слово состоит из 5 букв. Сколько неудачных попыток может быть сделано человеком, не знающим секретного слова?

Решение. Общее число комбинации равно . Значит, неудачных попыток может быть 248831. Впрочем, обычно сейфы делают так, что после первой же неудачной попытки открыть их раздается сигнал тревоги.

Задача 2. Найти количество всех пятизначных чисел.

Решение. Введем пять множеств: , . Согласно правилу прямого произведения получаем .

Задача 3. При игре в кости бросаются две кости и выпавшие на верхних гранях очки скла­дываются. Какова вероятность выбросить 12 очков?

Решение. Всего возможно различных исходов. Из них только один (6 + 6) дает двенадцать очков. Вероятность 1/36.

Размещения без повторений

Задача 1. Сколькими способами можно рассадить 4 учащихся на 25 местах?

Решение. Искомое число способов равно числу размещений из 25 по 4:

.

Задача 2. Учащемуся необходимо сдать 4 экзамена на протяжении 8 дней. Сколькими спосо­бами это можно сделать?

Решение. Искомое число способов равно числу 4-элементных последовательностей (дни сдачи экзаменов) множества из 8 элементов, то есть способов. Если известно, что по­следний экзамен будет сдаваться на восьмой день, то число способов равно .

Задача 3. В хоккейном турнире участвуют 17 команд. Разыгрываются золотые, серебряные и бронзовые медали. Сколькими способами могут быть распределены медали.

Решение. 17 команд претендуют на 3 места. Тогда тройку призеров можно выбрать способами .

Перестановки без повторений

Задача 1. Сколькими способами можно разме­стить на полке 4 книги?

Решение. Искомое число способов равно числу способов упорядочения множества, состоящего из 4 элементов, т. е. .

Задача 2. Сколькими способами можно упоря­дочить множество так, чтобы каждое четное число имело четный номер?

Решение. Четные числа можно расставить на местах с четными номерами (таких мест ) спосо­бами; каждому способу размещения четных чисел на местах с четными номерами соответствует способов размещения нечетных чисел на местах с нечетными номерами. Поэтому общее число перестановок ука­занного типа по правилу умножения равно .

Задача 3. Сколько можно составить перестано­вок из элементов, в которых данные 2 элемента не стоят рядом?

Решение. Определим число перестановок, в ко­торых данные два элемента и стоят рядом. Могут быть следующие случаи: стоит на первом месте, стоит на втором месте, ..., стоит на -м ме­сте, а стоит правее ; число таких случаев равно . Кроме того, и можно поменять местами, и, следовательно, существует способов разме­щения и рядом. Каждому из этих способов соот­ветствует перестановок других элементов. Следовательно, число перестановок, в которых и стоят рядом, равно . Поэтому искомое число перестановок равно .

Задача 4. Сколькими способами можно распо­ложить на шахматной доске 8 ладей так, чтобы они не могли бить друг друга?

Решение. При указанном расположении ладей на каждой вертикали и каждой горизонтали стоит лишь одна ладья. Рассмотрим одно из таких располо­жений ладей. Пусть — номер вертикали, в которой стоит ладья из первой горизонтали, — номер верти­кали, в которой стоит ладья из второй горизонта­ли, ..., — номер вертикали, в которой стоит ладья из последней, восьмой, горизонтали. Тогда есть некоторая перестановка чисел 1, ..., 8. Среди чи­сел нет ни одной пары равных, иначе 2 ла­дьи попали бы в одну вертикаль. Следовательно, каж­дому расположению ладей соответствует определен­ная перестановка чисел 1, ..., 8. Наоборот, каждой перестановке чисел 1, ..., 8 соответствует такое рас­положение ладей, при котором они не бьют друг дру­га. Следовательно, число искомых расположений ла­дей равно .

Сочетания без повторений

Задача 1. Сколькими способами читатель может выбрать 3 книги из 5?

Решение. Искомое число способов равно числу 3-элементных подмножеств 5-элементного мно­жества:

.

Задача 2. Сколькими способами из 7 человек можно выбрать комиссию, состоящую из 3 чело­век?

Решение. Чтобы рассмотреть все возможные комиссии, нужно рассмотреть все возможные 3-элементные подмножества множества, состоящего из 7 человек. Искомое число способов равно

.

Задача 3. В турнире принимали участие шахматистов, и каждые 2 шахматиста встретились 1 раз. Сколько партий было в турнире?

Решение. Партий было сыграно столько, сколько можно выделить 2-элементных подмножеств в множестве из элементов, то есть

.

Задача 4. В скольких точках пересекаются диагонали выпуклого -угольника, если никакие 3 из них не пересекаются в одной точке?

Решение. Каждой точке пересечения двух диагоналей соответствует 4 вершины -угольника, а каждым 4 вершинам -угольника соответствует 1 точка пересечения (точка пересечения диаго­налей четырехугольника с вершинами в данных 4 точках). Поэтому число всех точек пересечения равно числу способов, которыми среди вершин можно выбрать 4 вершины:

.

Задача 5. В начале игры в домино каждому играющему выдается 7 костей из имеющихся 28 различных костей. Сколько существует различных комбинаций костей, которые игрок может получить в начале игры?

Решение. Очевидно, что искомое число равно числу 7-элементных подмножеств 28-элементного множества. Имеем:

.

Сочетания с повторениями

Задача 1. Трое ребят собрали в лесу 63 яблока. Сколькими способами они могут разделить их между собой?

Решение. Поставим в соответствие каждому делению яблок между ребятами сочетание с повторениями следующим способом. Типами элементов в нашем случае будут ребята. Таким образом, имеем три типа элементов (), из которых предстоит составить все различные расстановки длины . Наличие в расстановке какого-либо из элементов отвечает принадлежности данного яблока соответствующему мальчику. Порядок элементов в такой расстановке не играет роли. При делении яблок между ребятами не важно, какое из них попадет тому или иному мальчику. Тогда число способов разделить яблоки между ребятами равно .

Задача 2. Сколькими способами можно рассадить вновь прибывших гостей среди го­стей, уже сидящих за круглым столом?

Решение. Очевидно, что между сидящими за круглым столом гостями имеется промежутков, в которые можно рассаживать вновь прибывших. Таким образом, это можно сделать способами.

Задача 3. Сколько целых неотрицательных решений имеет уравнение

?

Решение. Если имеем целые неотрицательные числа такие, что , то можем составить сочетание из элементов по с повторениями взяв элементов первого типа, — второго типа, ..., — -го типа. Наоборот, имея сочетание из элементов по , получим решение уравнения элементов первого типа, — второго типа, ..., — -го типа) в целых неотрицательных числах. Следовательно, существует биекция между множеством всех сочетаний из элементов по с повторениями и множеством всех целых неотрицательных решений уравнения . Поэтому число решений равно .

Перестановки с повторениями

Задача 1. Сколько различных слов можно составить, переставляя буквы слова «Уссури»?

Решение. .

ГРАФЫ

Отношение-схему, приведенную в предыдущем разделе на рис. 3,b, графически можно изобразить разными способами:

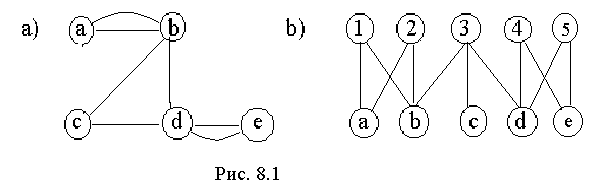
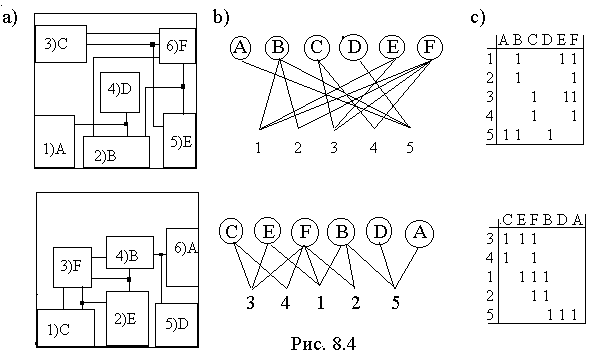
Рис. 1,а показывает, какие из элементов схемы соединены друг с другом и сколькими связями. На рис.1,b элементы и связи между ними представлены как равноправные сущности, образующие единую систему. Представленные изображения являются примерами графов - математических объектов, которые можно определить следующим образом.

Графом G = (V, E) называется совокупность множеств вершин V={v₁,v₂,...,v_n} и соединяющих их ребер Е = {e₁, e₂,..., e_m}. Ребро e_k = (v_i, v_j) соединяет вершины v_i и v_j. Графы являются скорее «топологическими», чем «геометрическими» объектами, т.е. oни выражают больше отношения между вершинами, чем взаимное расположение вершин и ребер на плоскости. Таким образом, граф может быть изображен бесконечным количеством разных, но эквивалентных способов. Например, переставив на рис. 8.1 крайние элементы a и е, получим более путаные изображения той же схемы (с переобозначенными вершинами):

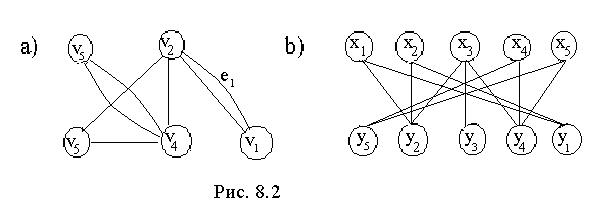
Две вершины графа называются смежными, если они соединены ребром (инцидентны ребру). Два ребра называются смежными, если они имеют общую вершину (инцидентны ей).

Граф называется планарным, если его можно изобразить на плоскости с непересекающимися ребрами. Граф, представленный на рис. 1-2,а - планарный; граф на рис. 1-2,b - нет. Исследование планарности, или же насколько близок граф электронной схемы планарному, представляет интерес при проектировании печатных плат для предотвращения пересечения неизолированных проводников.

Граф G = (V, E) = (X,Y, E) называется двудольным, если существует такое разбиение множества V его вершин на два непересекающихся подмножества Х и Y: V = X È Y, что никакие две вершины из Х или из Y не являются смежными (см. рис. 1-2, b).

Графы, как симметричные отношения, кодируются квадратными матрицами смежности М = (m_ij)^n´n, где n - число вершин, а элемент m_ij равен числу ребер, связывающих i-e и j-е вершины (элементы М симметричны относительно главной диагонали: m_ij = m_ji). Для графа на рис. 1,а имеем:

	a	b	C	d	e				a	b	c	d	e
	0	2	0	0	0	a			1	1	0	0	0	1
	2	0	1	1	0	b			1	1	0	0	0	2
M=	0	1	0	1	0	c		N=	0	1	1	1	0	3
	0	1	1	0	2	d			0	0	0	1	1	4
	0	0	0	2	0	e			0	0	0	1	1	5

Двудольный граф рис. 1,b кодируется несимметричной матрицей N, у которой ненулевой элемент n_{i j}=1 указывает на связь i-й вершины из Х с j-й вершиной

из Y.

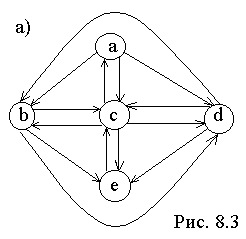
Рассмотрим предложенную фон Нейманом схему ЭВМ, которая состоит из множества устройств {a, b, c, d, e}, где a - устройство ввода, b - арифметическое устройство, с - устройство управления, d - запоминающее устройство, е - устройство вывода. Поступление информации из i-го устройства в j-е можно представить в виде ориентированного графа (рис. 3,а) и соответствующей ему матрицы смежности, которая, вообще говоря, не будет симметричной поскольку каждому ребру графа теперь предписывается определенное направление, обозначаемое стрелкой.

b)

а b c d e

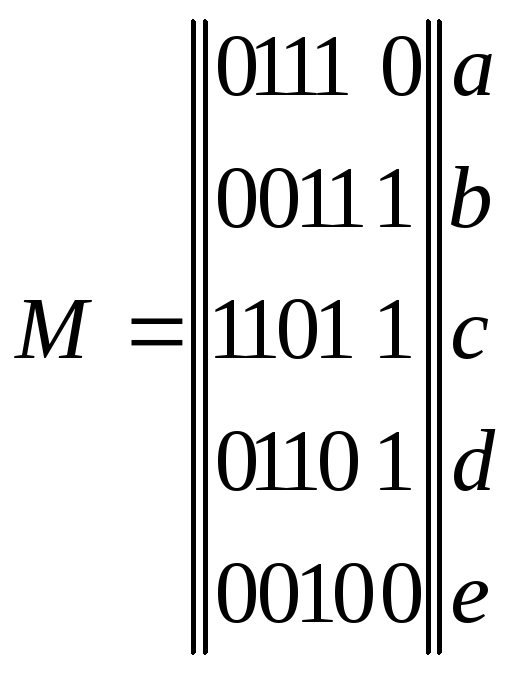
Ориентированные графы можно ассоциировать с несимметричными отношениями. Сфера их применения - потоки данных в информационных сетях, транспортные сети с направленными магистралями.

Рассмотрим задачу топологического проектирования БИС, целью которой является размещение на кристалле-чипе элементов схемы и проведение (трассировка) соединений-цепей.

На рис. 4,а приведены два решения для одной и той же схемы, соответствующие изображениям двудольного графа (рис. 4,b) и матрицам смежности (рис. 8.4,с: нулевые элементы не изображены).

Алгоритм топологического проектирования поочередно размещает элементы БИС в указанном порядке, начиная с левого нижнего угла чипа. Оптимальное упорядочение размещаемых элементов с учетом их связности приводит к более компактной реализации схемы, минимизирующей суммарную длину цепей и число их пересечений. Искомая последовательность элементов и цепей может быть получена соответствующей перенумерацией вершин двудольного графа (рис. 4,b) таким образом, чтобы связные вершины располагались как можно ближе друг к другу (что эквивалентно минимизации суммарной длины ребер в соответствующем изображении графа).

Итеративный алгоритм упорядочения по связности вершин двудольного графа G = (X,Y, E) заключается в поочередной фиксации одного из семейств вдоль координатной оси и перемещении каждой вершины другого семейства в геометрический центр координат связанных с ней вершин противоположного семейства. Пусть X_j^k и Y_i^k - координаты на k-й итерации вершин X_jÎX и Y_iÎY; j=0,1,...n; i=0,1,...,m. Положим вначале X_j⁰ = j. Пусть инцидентны вершинеY_i, а инцидентны вершинеХ_j, тогда k-я итерация алгоритма, проводящая поочередную коррекцию вершин обоих семейств, запишется в виде следующих этапов:

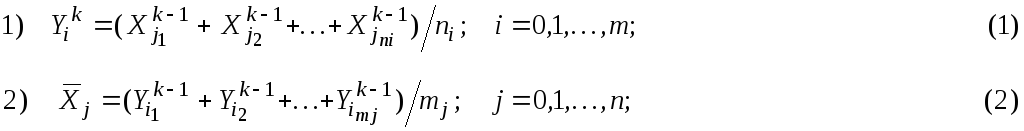
Для предотвращения стягивания решения в точку координаты вершин Х_j нормируются так, чтобы их крайние значения попадали на границы интервала [0,n]:

Итерации прекращаются поcле достижения заданного уровня стабилизации:

после чего проводится сортировка последовательностей X_j^k и Y_i^k в порядке возрастания который и задает искомое упорядочение вершинG.

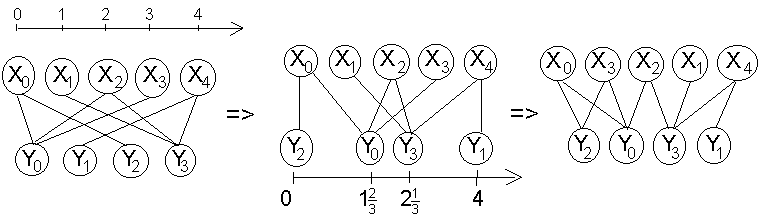
На рис. 5 приведен пример упорядочения графа за одну итерацию.

1) 2)

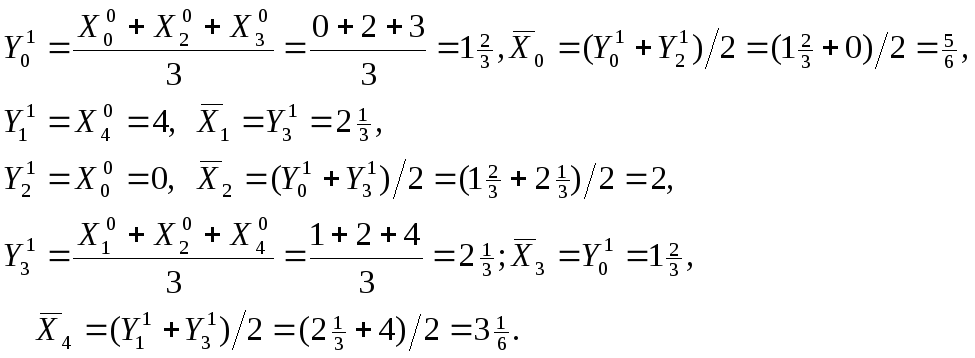
Рис. 5

Упорядочение вершин двудольного графа эквивалентно приведению его матрицы смежности к ленточному виду, в котором ненулевые элементы сосредотачиваются возле главной диагонали (см. также рис. 4,с):

	X0 X1 X2 X3 X4			X0 X3 X2 X1 X4
Y0 Y1 Y2 Y3	1 1 1 1 1 1 1 1	Þ	Y2 Y0 Y3 Y1	1 1 1 1 1 1 1 1

Разрешив элементам матрицы смежности принимать не только крайние, но и промежуточные значения из интервала [0,1], мы придем к понятию нечеткого графа, у которого связь между вершинами может носить не только однозначный, но и предположительный характер, как например, на рис. 6.

Вернемся к работе службы знакомств. В отличие от эгоистических желаний конкретных клиентов (требующих себе чего получше, а остальным - что останется) цель службы - организовать как можно больше перспективных пар.

	X0	X1	X2	X3	X4
Y0	1	0,7	0,7	0,3	0
Y1	1	1	1	0,7	0,3
Y2	0	0,7	1	1	1
Y3	0	0	0,3	0,7	1

Рис.6

Поэтому матрицы индивидуальных предпочтений женихов и невест в конце главы 6 целесообразно слить в итоговую матрицу - нечеткий граф, задающий суммарную близость i-го клиента j-й клиентке как среднеарифметическое значение их индивидуальных предпочтений (рис. 7,а)

а)		Г	Д	Е	Ж		b)		Д	Г	Ж	Е
	А	0,85	0,1	0,1	0,6			Б	0,55	0,1	0,1	0
	Б	0,1	0,55	0	0,1	=>		А	0,1	0,85	0,6	0,1
	В	0,25	0,2	0.8	1			В	0,2	0,25	1	0.8

Рис. 7

Аналогом упорядочения вершин нечеткого двудольного графа будет перенумерация строк и столбцов его матрицы из условия: чем больше значение элемента - тем ближе он должен быть к главной диагонали (рис. 6, 7,b). Формально эту цель можно описать как задачу минимизации функции (m+1)(n+1) переменных

(3)

где m_ij - элемент матрицы нечеткого графа, определяющий степень связности i-й вершины с j-й; x_j и y_i - номера (координаты) переупорядочиваемых строк и столбцов.

Сняв ограничения на целочисленность координат X_j и Y_i, разрешим строкам и столбцам располагаться произвольным образом на плоскости. В этом случае, однако, (3) дает тривиальное решение J_min = 0 при x_j = y_i "i,j. Для предотвращения стягивания строк и столбцов в точку, введем ограничение:

(4)

Метод проекции градиента для задачи условной оптимизации (3-4) может быть оформлен в виде итерационного процесса с начальным приближением k-я итерация которого имеет вид:

, i = 0,1,...,m;

,

j= 0,1,...,n.

Формулы (1-2) алгоритма упорядочения вершин четкого графа отсюда получаются, как частный случай при целых m_ij Î {0,1}.