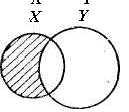
Операция определения разности множеств

Данная операция, в отличие от операций объединения и пересечения, определяется только для двух множеств.

Разность множеств – множество, состоящее из всех тех и только тех элементов, которые принадлежат одному множеству и не принадлежат другому.

Рис. 3

Разность множеств X и Y, обозначаемая через , фор­мально определяется как ={x│xX и xY } и может быть пояснена рис. 3 с использованием диаграмм.

Примеры:

1) Если Х={1, 2, 3, 4, 5} и Y={2, 4, 6, 7}, то X\Y={1, 3, 5} и Y \Х={6, 7}.

2) Если X – множество отличников в группе, Y – множество студентов, проживающих в общежитии, то Y \Х – множество отличников, не проживающих в общежитии.

Операция определения дополнения множества.

Дополнение множества X (до универсального множества I) – множество , определяется из соотношения =I\Х.

Формальное определение ={x│xX и xY }.

Так например, если I={1, 2, 3, 4, 5, 6, 7} и Х={3, 5, 7}, то ={1, 2, 4, 6}.

I Рис. 4

Универсальное множество удобно изображать графически (рис. 4) в виде множества точек прямоугольника. Отдельные области этого прямоугольника означают различные подмножества универсального множества.

Изображение множества в виде областей в прямоугольнике, представляющем универсальное множество, называют диаграммой Эйлера-Венна.

На рис. 4 множество представляет собой незаштрихованную область.

Так как X ине имеют общих элементов, то = _.

Кроме того, = I и .

С помощью операции дополнения можно в удобном виде представить разность множеств:

={x│xX и xY }={x│xX и x},

то есть =.

Тождества алгебры множеств

С помощью операций объединения, пересечения и до­полнения из множеств можно составлять различные алге­браические выражения, которые бывают очень полезны при преобразованиях алгебраических выражений над множествами.

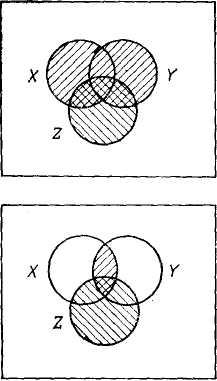
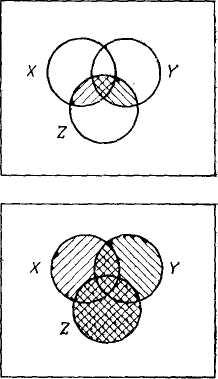
С использованием диаграмм Эйлера-Венна, из которых видно, что левые и правые части алгебраических выражения, составленных из множеств X, Y и Z, определяют одно и то же множество, может быть подтверждена справедливость того, что следующих наиболее часто используемых тождеств:

; (закон повторения)

; ;	тождества де-Моргана

;

.

	а) б)
Рис. 5 Геометрическая иллюстрация тождеств (а) и (б)

Операция проецирования кортежа

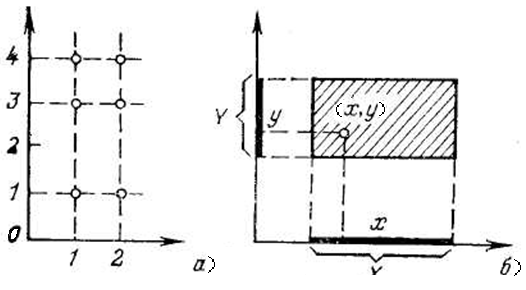
Кортеж (a₁,a₂) может рассматриваться как точка на плоскости (рис. 6,а) или как вектор, проведенный из начала координат в данную точку.

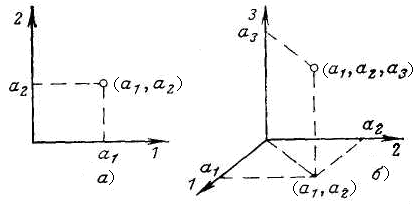
Рис. 6 Проекции двух- и трёхэлементного кортежей

Компоненты a₁ и a₂ будут проекциями векто­ра на оси 1 и на оси 2:

Пp₁(a₁,a₂) = a₁; Пр₂(a₁,a₂) = a₂.

Кортеж (a₁,a₂,a₃) может рассматриваться как точка в трехмерном пространстве или как трехмерный вектор, проведенный из начала координат в эту точку (рис. 6,б).

Проекции вектора на оси координат

Пр_i (a₁,a₂,a₃) = a _i , i = 1, 2, 3.

Однако в данном случае можно также говорить о проекции кортежа сразу на две оси, например 1 и 2, т. е. на коорди­натную плоскость. Нетрудно видеть, что эта проекция представляет собой двухэлементный кортеж

Пр₁₂(a₁,a₂,a₃) = (a₁,a₂).

Обобщая эти понятия, будем рассматривать упорядоченное п-элементное множество вещественных чисел a=(a₁,…,a_n) как точку в воображаемом п-мерном пространстве, называемом иногда гиперпространством, или п-мерным вектором. При этом компоненты п-элементного кортежа а будем рассматривать как проекции этого кортежа на соответствующие оси

Пр_i a = a _i , i=1,..., п.

Если i, j,..., k – номера осей, причем 1 i, j,..., k п, то проекция кортежа а на оси i, j,..., k будет

Пр _{i, j,...,k} a = (a_i,a_j,…,a_k).

Операция определения прямого произведения множеств

Прямое произведение множеств X и Y называют множество, обозначаемое X×Y и состоящее из всех тех и только тех упорядоченных пар, первая компонента которых принадлежит множеству X, а вторая – множеству Y.

Таким образом, элементами прямого произведения являются двухэлементные кортежи вида (х,у).

Формаль­ное определение

X×Y ={(x,y)│xX, yY}. (2.41)

Рис. 7	Пример. Пусть Х={1, 2}, Y ={1, 3, 4}. Тогда X×Y ={(1, 1), (1, 3); (1, 4), (2, 1), (2, 3), (2, 4)}. Геометрическое представление этого множества приведено на рис. 8. Пример. Пусть X и Y – отрезки вещественной оси. Прямое произведение X×Y изобразится заштрихованным прямоугольником (рис. 8). Из этого рисунка следует, что свойства прямого произведения отлича­ются от свойств обычного произведе­ния в арифметическом смысле.

В частности, прямое произведение изменяется при изме­нении порядка сомножителей, т. е.