Алгебра предикатов

Рассмотрим истинное высказывание « 5 - целое число » и ложное высказывание « целое число ». Общую часть их можно выделить как предложение-шаблон « - целое число », при подстановке в который конкретного числа получается конкретное высказывание. Введя обозначение : Р(х) = « х - целое число », получим P(5) = 1; P( ) = 0 . Теперь пусть Р(х) = « x - овощ ». Замещая х на конкретные плоды, получаем истинное высказывание Р(ЛУК)=1, или ложное: P(СЛИВА) = 0 .

Назовем предикатом Р(х) предложение, зависящее от переменной х, принадлежащей некоторой предметной области - множеству U: xU. В первом примере хR, во втором U - это множество плодов. При подстановке фиксированного элемента аU предикат Р(х) превращается в высказывание Р(а){0,1}. Таким образом, предикат можно считать логической функцией, определенной на элементах множества U произвольной природы.

U разбивается предикатом Р(х) на два непересекающихся подмножества: на первом из них , которое назовем множеством истинности , предикат принимает истинные значения, на втором - ложные. Обозначив их через Р и Р, соответственно, получим: U = P P.

На рис. 4.1 прямоугольная область U представлена в виде объединения двух непересекающихся частей.

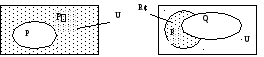
Рис. 4.1 Рис. 4.2

Рассмотрим в качестве предиката Р(х), определенного на множестве вещественных чисел, уравнение: x ²  4x = 0. В данном примере P = {0, 2}; P= R\P.

К предикатам применимы все логические операции. Для предиката-отрицания множеством истинности будет заштрихованная область.

Применяя импликацию к предикатам Р(х) и Q(x), получим новый предикат

R(x) = P(x) Q(x). На рис. 4.2 заштриховано множество R¢ = P\Q (так как при

х_о Î R¢ имеем Р(х_о) = 1, Q(x_o) = 0, следовательно, высказывание Р(х_о)®Q(x_o) ложно).

Рассмотрим предложения:

«Cуществуют х такие, что | х отрицательно »,

«Для любого z | z удалено от начала координат на расстояние r ».

В обеих фразах фрагменты справа от вертикальной черты являются предикатами. В целом же обе фразы образуют высказывания, зависящие не от входящих в них переменных, а от области определения xиz. Первое предложение истинно на всех вещественных числах, а второе только, если областью определенияzявляются точки окружности Г. Сокращенно оба высказывания можно записать так:

$х х<0, x Î R. "z |z|<r, z Î Г Ì R².

Здесь использованы квантор существования $, соответствующий словам «существует», «найдется», «хотя бы один», и квантор общности", соответствующий словам «для любого», «все», «каждый». Таким образом, кванторы связывают предикатные переменныех, z, превращая предикатыР(х) иQ(x) в высказывания:

$x P(x); "zQ(z).

Опишем с помощью предиката метод математической индукции, доказывающий истинность высказывания "n P(n), определенного на всех натуральных числах nÎN, в два этапа:

1. Проверяется истинность P(n) при n=1;

2. Из предположения истинности P(k) для k>1 доказывается истинность P(k+1).

Докажем, например, неравенство Бернулли:

(1+ a)ⁿ ³ 1 + na, "n, a>-1.

1. Проверяем Р(1): (1+a)¹ ³ 1+1×a;

2. Предполагаем P(k): (1+a)^k ³ 1+ka; умножаем обе части на 1+a >0:

(1+a)(1+a)^k ³ (1+ka)(1+a) = 1 + ka + a + ka² ³ 1 + ka + a;

приведя крайние части цепочки неравенств к требуемому виду, получаем истинность P(k+1): (1+a)^k+1³ 1+(k+1)a, что и доказывает истинность "n P(n).

Применение отрицания к высказываниям с кванторами сводится к смене квантора и отрицанию связываемого предиката:

.

Проверим эту эквивалентность. Пусть левое высказывание истинно, тогда

$x P(x) - ложно Þ =1 всегдаÞ "X ; аналогично проверяется, что ложность левой части влечет за собой ложность правой части.

Таким же образом доказывается эквивалентность:

¨ $x

и другие формулы исчисления предикатов.

Рассмотренные предикаты называются одноместными, так как они зависят только от одной переменной. Неравенство х < уможно считать двухместным предикатомP(x,y), содержащим две предметные переменные, определенные на декартовом произведенииR´R=R². Область истинностиР(х,у) - полуплоскость, ограниченная сверху прямойу = х.

Предложение, определенное на множестве Х₁´ Х₂´...´X_n называют

n-местным предикатом: P(x₁, x₂,... x_n), x₁ÎX₁, ... x_nÎX_n .

Найдем область истинности трехместного предиката P(x,y,z) = (xy < z), определенного на тройках (x, y, z) Î A´A´A = A³, где А = {1,2,3,5}.

Число всех упорядоченных троек из четырехэлементного множества А равно 4×3×(4-3+1) = 24. Для сокращения перебора используем симметричность предиката относительно первых двух переменных: P(x,y,z) = (xy < z) = (yx < z) = P(y,x,z). Далее, для выполнения неравенства необходимо, чтобы правая часть z превосходила каждый из сомножителей x,y. С учетом сказанного, имеем 3 благоприятных случая: 1×2 < 3, 1×2 < 5, 1×3 <5, дающие 6 элементов области истинности Р:

P(1,2,3) = (2<3) = P(2,1,3), P(1,2,5) = (2<5) = P(2,1,5), P(1,3,5) = (3<5) = P(3,1,5).

Итак, область истинности Р образует множество троек: {(1,2,3), (1,2,5), (1,3,5),

(2,1,3), (2,1,5), (3,1,5)}.

Многоместные предикаты позволяют компактно описать сложные определения математического анализа. Например, сходимость последовательности x_n к предельному значению a выглядит так:

"e>0 $N "n: n>N ® |x_n-a| < e.

Для случая lim () =a = 2 введем в рассмотрение 4-местный предикат:

Р(e, N, n, a) = (n>N ® |- a| < e).

После «навешивания» трех кванторов он обращается в одноместный:

("e>0 $N "n P(e, N, n, a)) = Pr(a),

областью истинности которого является единственный элемент 2: Pr(2)=1.

В общем случае, связывая любую из предметных переменных квантором, или заменяя ее предметной постоянной, мы снижаем число мест в предикате на единицу. Например, из двухместного предиката Р(х,у) с помощью двух кванторов можно образовать 8 высказываний:

"x "y P(x,y) ¨ "y "x P(x,y),

$x $y P(x,y) ¨ $y $x P(x,y),

$x "y P(x,y) -® "y $x P(x,y),

"x $y P(x,y) $y "x P(x,y),

только два первых из которых равносильны, так как разноименные кванторы переставлять нельзя. Приведем еще некоторые общезначимые формулы алгебры предикатов:

"x P(x) Ù "x Q(x) ¬® "x [P(x) ÙQ(x)],

"x P(x) ® P(a).

Последнюю формулу иллюстрирует пословица «все кошки ночью серы» :

если P(кошка) = (кошка ночью сера), то Р(МУРКА) = (МУРКА ночью сера).

Формулы, подобные приведенным и ранее рассмотренным, входят в исчисление предикатов, являющееся расширением и обобщением исчисления высказываний. В отличие от последнего теперь в логические рассуждения можно вовлекать переменные трех видов. Например, в формулу q ® $x P(x,y) входят:

1. булева переменная q Î {0, 1};

2. элемент произвольного множества у Î М;

3. предикатная переменная Р.

Алгебра предикатов является мощным инструментом проверки и автоматизации математических рассуждений. Сферой современного ее применения являются сложные системы управления, базы знаний, экспертные системы.