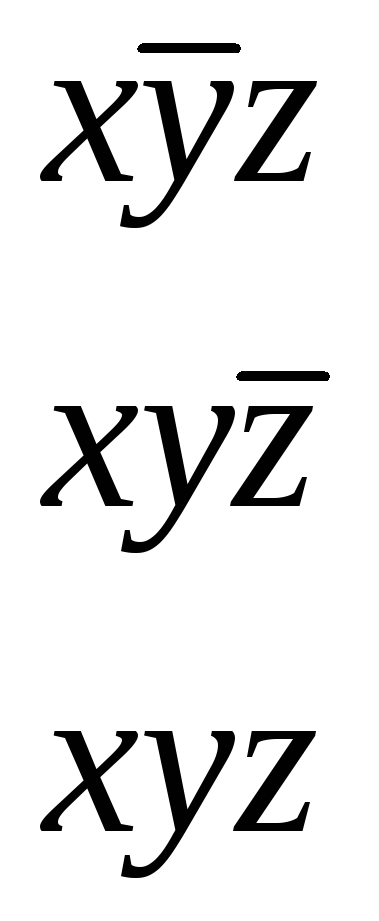X×y y×X.

Операция прямого произведения легко распространяется и на большее число множеств. Прямым произведением множеств X1,X2,...,Xk называют множество, обозначаемое X1×X2×...×Xk и состоящее из всех тех и только тех кортежей длины k, первая компонента которых принадлежит X1, вторая X2, и т. д.

Если R – множество вещественных чисел, то R×R представляет собой вещественную плоскость, a R×R×R трёхмерное вещественное пространство.

Операция проецирования множества

Операция проектирования множества тесно связана с операцией проектирования кортежа и может применяться лишь к таким множествам, элементами которых являются кортежи одинаковой длины.

Проекция множества М, состоящего из кортежей одинаковой длины – множество проекций кортежей из М.

Пример. Пусть М ={(1, 2, 3, 4, 5), (2, 1, 3, 5, 5), (3, 3, 3, 3, 3), (3, 2, 3, 4, 3)}. Тогда Пр₂М ={2, 1, 3};

Пр₂,₄М = {(2, 4), (1, 5), (3, 3)}.

АЛГЕБРЫ ЛОГИКИ

Булевой алгеброй назовем множество В вместе с тремя операциями Бинарные операции: +,× и унарная операция вместе с двумя элементамиВ, которые обозначаются символами 0 и 1, удовлетворяют нижеследующим законам (в которых операция × опущена). Для всех x,y,z Î В :

1. a) x + 0 = x, б) x×1 = x;

2. a) x + y = y + x, б) xy = yx - коммутативность;

3. a) x + (y+z) = (x+y) + z, б) х (yz) = (xy) z - accoциативность;

4. a) x (y+z) = xy + xz, б) x + yz = (x+y) (x+z) - дистрибутивность;

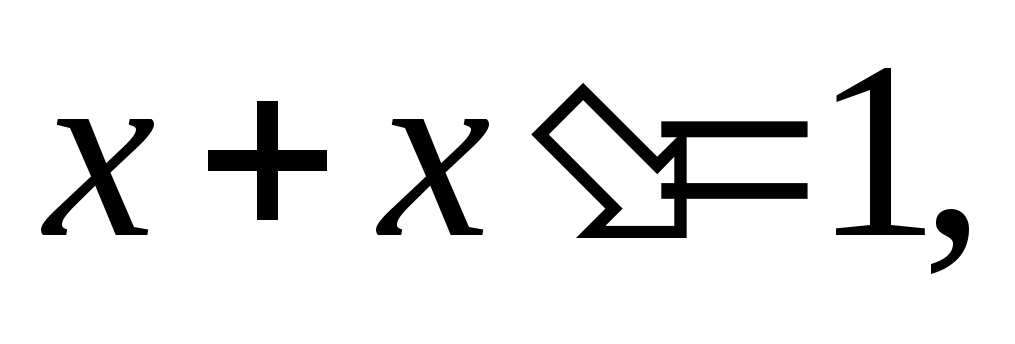5. a) б)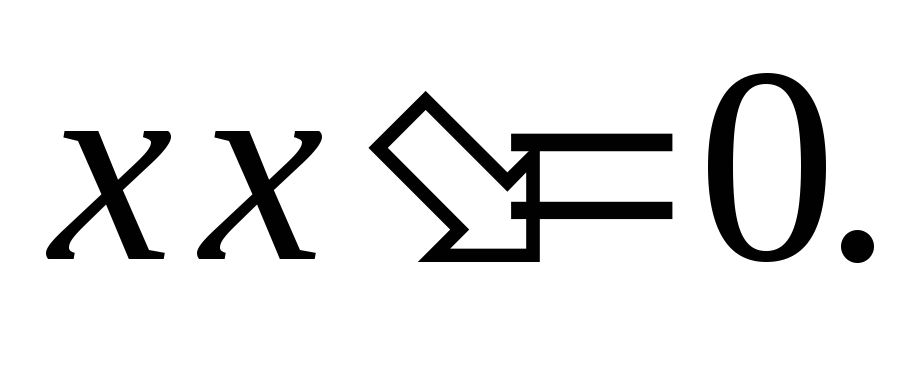- комплементарность.

В начале списка следуют тождества, обычные для числовой алгебры (заметим, что эти очевидные законы выполняются не во всех алгебрах, например, для матриц А и B АВ ¹ ВА !). Специфичными являются дистрибутивный закон (4.б) и законы (5), характеризующие элемент-дополнение . Следующие, получаемые из аксиом соотношения особенно часто используются в булевых вычислениях:

6. a) x + 1 = 1, б) x×0 = 0;

7. a) x + x = x, б) хх = х - идемпотентность;

8. a) x + xy = x, б) х (x+y) = x - поглощение;

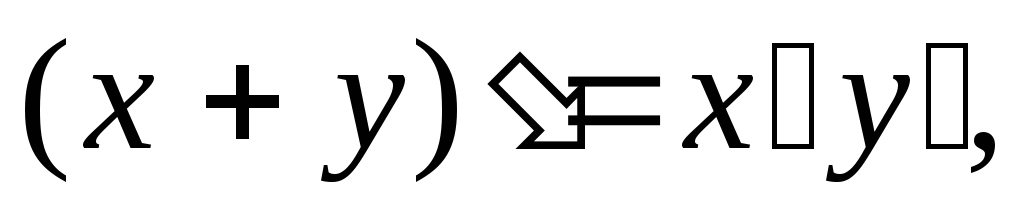9. a) б)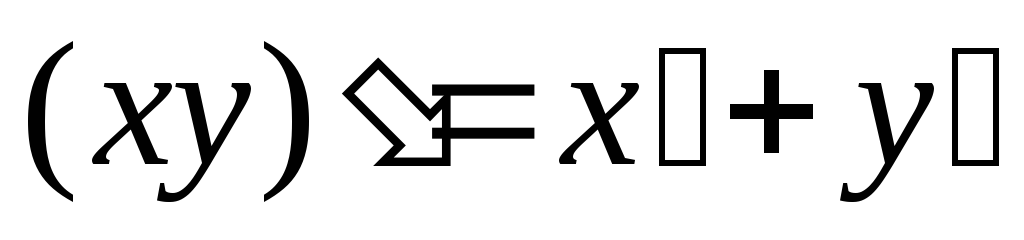- законы де Моргана;

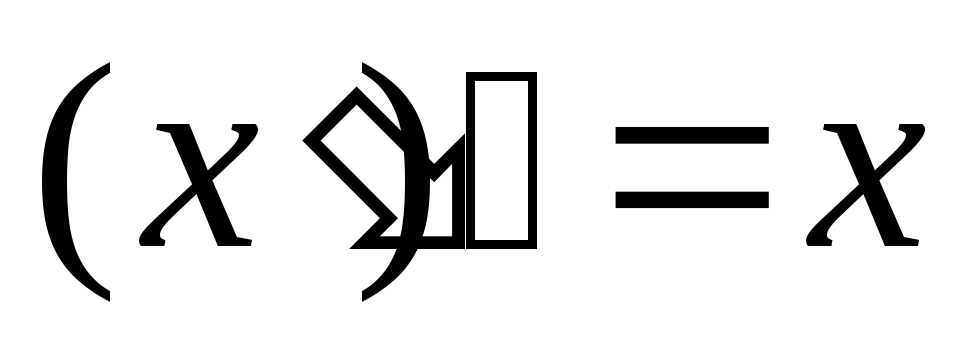6. - двойное дополнение.

В отличие от числовых операций сложения и умножения булевы операции + и × симметрично входят в тождества 1-9. Если в выписанных тождествах взаимно

заменить символы + и, а также 0 и 1, то получится то же самое множество тождеств. На этом основан принцип двойственности для булевых алгебр: если доказана истинность некоторого утверждения, то истинным будет и двойственное утверждение, то есть, то, которое получается из данного взаимной заменой символов + и, а также 0 и 1. Например, доказав тождество мы можем быть уверены в тождестве. Рассмотрим примеры булевых алгебр.

1. Операции над множеством В из двух элементов:

В = {0,1} (1 - истина, 0 - ложь). Поскольку логические переменные принимают только два значения, операции над ними однозначно определяются в виде таблиц истинности для сложения Ú, умножения Ù и отрицания:

p	q	pÚq		p	q	pÙq		p
0 0 1 1	0 1 0 1	0 1 1 1		0 0 1 1	0 1 0 1	0 0 0 1		0 1	1 0

последний столбец таблицы -результат операции над каждым из возможных наборов операндов (представляющим двоичное представление номера соответствующей строки). При построении таблицы истинности сложных формул промежуточные результаты выстраиваются слева направо в виде промежуточных столбцов. Например, для левой и правой частей тождества (4.б):

pÚ qr = (pÚq)(pÚr)

таблицы истинности (в которых число строк теперь будет равно числу трехразрядных двоичных наборов - 2³ = 8) примут вид:

p	g	r	gr	pÚgr		p	g	R	pÚg	pÚr	(pÚg) (pÚr)
0 0 0 0 1 1 1 1	0 0 1 1 0 0 1 1	0 1 0 1 0 1 0 1	0 0 0 1 0 0 0 1	0 0 0 1 1 1 1 1		0 0 0 0 1 1 1 1	0 0 1 1 0 0 1 1	0 1 0 1 0 1 0 1	0 0 1 1 1 1 1 1	0 1 0 1 1 1 1 1	0 0 0 1 1 1 1 1

Cовпадение двух последних столбцов в таблицах доказывает справедливость (4.б). Аналогичным образом можно проверить все тождества (1-10) для всех значений логических переменных.

2.Множество P всех подмножеств универсального множества I, включая само I и пустое множество , образует булеву алгебру с нулеми единицейI, операциями сложения È, пересечения Ç и дополнения ¢. Подсчитаем число элементов P в случае конечного множества I, содержащего n элементов. При n=1, I= {a} имеем два подмножества: P = {, {a}} ; при n=2, I = {a,b} число подмножеств удвоится: P = {,{a}, {b}, {a,b}}. При n=3 и I = {a,b,c} P будет содержать перечисленные ранее подмножества и еще столько же, полученных добавлением к каждому из них нового элемента с. Таким образом, при увеличении n на единицу число подмножеств I будет удваиваться, следовательно, P будет содержать 2ⁿ элементов.

В алгебре множеств закон (1.a): означает, что при объединении с пустым множеством ничего не изменится; закон (7.б):означает, что пересечениеА с самим собой совпадает с А. Помимо тождеств (1-10) в теории множеств имеет место ряд законов, связанных с включением одного множества в другое. Например, если А Ì В и В Ì С, то А Ì С; если А Ì С, то соотношениеэквивалентно

Булевы операции над множествами приводят к построению объектов того же сорта - подмножеств универсального множества I. Сейчас будет изложен способ конструирования более сложных множеств, «вылезающих» за пределы I. Рассмотрим множество размеченных клеток шахматной доски, множество С столбцов, которые обозначим буквами a, b,...,h и множество S строк от 1 до 8. Каждая клетка может быть однозначно задана двумя символами: один из множества С={a, b,...,h}, другой из множества S = {1,2,...,8}, например, e2,e4, h8. Таким образом, из множеств С и S мы образовали множество С´S всех клеток доски.

Декартовым произведением А´В множеств А и В называется множество упорядоченных пар элементов из А и В:

A´B={(a,b): aÎA, bÎB}.

Приведем примеры. Пусть X = {0,1}, Y = {x,y}, тогда X´Y = {(0,x), (0,y), (1,x), (1,y)}; Y´X = {(x,0), (x,1), (y,0), (Y,1)}, таким образом, X´Y ¹ Y´X, то есть, коммутативный закон не выполняется. Декартовым произведением числовой оси R (геометрического образа множества вещественных чисел) на самое себя будет плоскость R² = R´R.

Пусть даны n множеств A₁, A₂, ..., A_n. Множество всех упорядоченных

наборов (а₁, а₂, ..., а_n) таких, что а₁ÎА₁, а₂ÎА₂, ..., а_nÎА_n, называют декартовым произведением A₁´ A₂ ´ ... ´A_n . Например, множество разнообразных обедов из трех блюд в ресторане будет декартовым произведением трех меню для каждого из блюд. Декартово произведение R´R´R = {(x,y,z), x,y,zÎR} описывает бесконечное множество всех точек пространства R³.

3. Случайные события, связанные с некоторым экспериментом, образуют булеву алгебру относительно операции сложения А+В (наступление хотя бы одного из событий А, В), умножения АВ (одновременное появление А и В), перехода от А к противоположному событию (наступающему в точности при не появлении данного события). Кроме того, фиксируется невозможное (никогда не наступающее) событие, соответствующее булевому нулю, и достоверное (всегда наступающее при проведении данного эксперимента) событиеW, соответствующее булевой единице. Тождество (5.а) означает, что в результате опыта обязательно произойдет либо событие А, либо :A+=W; (5.б) означает, что А и одновременно произойти не могут:А=. Булева алгебра событий является исходным материалом для теории вероятности. Пусть экспериментW содержит n(W) исходов, cреди которых событию А благоприятствуют n(A) исходов, тогда вероятность наступления А равна р(А) = n(A) / n(W). Например, если W - бросание шестигранной игральной кости (n(W)=6), A - выпадание четной грани (n(A)=3), то р(А) = 3/6. Интерпретация события А как подмножества {2, 4, 6} универсального множества {1,2,3,4,5,6} всех исходов W, позволяет привлечь к вычислению вероятности сложных событий идеи булевой алгебры множеств.

Выведем формулу вычисления р(А+В) по известным вероятностям р(А), p(B), p(AB). Имеем:

n(A+B) = n(A) + n(B) - n(AB),

так как элементы, содержащиеся одновременно в А и в В, то есть, элементы АВ, считаются дважды при суммировании элементов А с элементами В. Деля обе части равенства на n(W), получим:

p(A+B) = p(A) + p(B) - p(AB).

Для трех слагаемых имеем: p[(A+B)+C] = p(A+B) + p(С) - р[(А+В)C]; закон (4.а)

дает: (A+B)C = AC + BC, отсюда

р[(А+В)C] = p(AC+BC) = p(AC) + p(BC) - p(АСВС).

C учетом равенств АСВС = АВСС = АВС (законы (2.б), (7.б)) окончательно получим:

p(A+B+C) = p(A) + p(B) + p(С) - p(AB) - p(AC) - p(BC) + p(ABC).

АЛГЕБРА ВЫСКАЗЫВАНИЙ

Подобно функциям математического анализа, например f(x,y,z) = x + yz, принимающим вещественные значения для x,y,z Î R, введем в рассмотрение функции нескольких булевых переменных, например, f(p,q,r) = pÚqr, принимающие вместе с аргументами только одно из двух значений: 0, или 1.

Рассмотрим набор n переменных (x₁, x₂,...,x_n), где x_i Î {0,1}, который назовем двоичным набором длины n. Число таких наборов равно 2ⁿ, поскольку при увеличении n на единицу будет происходить их удвоение (комбинирование каждого старого набора с новым нулем, или единицей). Назовем булевой функцией n переменных функцию, определенную на двоичных наборах длины n и принимающую на этих наборах значения 0, или 1. Так как область определения такой функции ограничивается 2ⁿ наборами значений аргументов, то ее можно однозначно описать Таблицей 1 из 2ⁿ строк. Правый столбец значений функции в таблице в свою очередь является двоичным набором длины 2ⁿ, следовательно, число булевых функций n аргументов равно числу всех таких наборов, т. е. . Например, существуют = 4 булевых функции j _к одного аргумента (табл. 2)

и = 2⁴ = 16 булевых функций y_к двух переменных х,у, представленных в табл. 3, которая содержит (как частный случай) четыре функции одного переменного:

j _o(x) º 0 º y_o(x,y);

j ₁(x) º x º y₅(x,y);

j ₂(x) º º y₁₀(x,y);

j ₃(x) º 1 º y₁₅(x,y).

Каждую из 16-ти функций можно отождествить с бинарной логической операцией. Отметим среди них 11-ю и 9-ю, имеющие особое смысловое значение. Импликация x®y, или логическое следование высказываний x и y, принимает ложное значение только в том случае, когда из истинной предпосылки х следует ложное заключение у; эквиваленция х«у принимает истинные значения только при совпадающих значениях операндов (см. табл. 4).

Таблица 1.														Таблица 3.
	x1	x2			…		xn-1			xn		f(x1 ,..., xn)		1 0 1 0	x
0 1 2 3 … 2n-1	0 0 0 0 … 1	0 0 0 0 … 1			… … … … … …		0 0 1 1 … 1			0 1 0 1 … 1		f(0,...,0,0) f(0,...,0,1) f(0,...,1,0) f(0,...,1,1) ............... f(1,...,1,1)		1 1 0 0	y
														0 0 0 0	y0(x,y) º 0
														1 0 0 0	y1(x,y) = x×y
														0 1 0 0	y2(x,y) =
														1 1 0 0	y3(x,y) = y
														0 0 1 0	y4(x,y) =
Таблица 2.														1 0 1 0	y5(x,y) = x
x	j 0		j 1			j 2			j 3					0 1 1 0	y6(x,y) =
0 1	0 0 1 1 0 1 0 1													1 1 1 0	y7(x,y) = x + y
														0 0 0 1	y8(x,y) =
Таблица 4.														1 0 0 1	y9(x,y) =
														0 1 0 1	y10(x,y) =
x y	x®y			x«y										1 1 0 1	y11(x,y) = x®y
0 0	1			1										0 0 1 1	y12(x,y) =
0 1	1			0										1 0 1 1	y13(x,y) =
1 0	0			0										0 1 1 1	y14(x,y) =
1 1	1			1										1 1 1 1	y15(x,y) º 1

C помощью таблицы истинности проверяется справедливость следующей замены: (1)

Покажем, как сложные высказывания, образованные с помощью произвольных логических операций, сводятся к формулам, включающим три основные операции – конъюнкцию, дизъюнкцию и отрицание.

Для произвольной бинарной функции f(x,y) справедливо тождество, проверяемое непосредственной подстановкой конкретных значений х и у:

.

C его помощью получается разложение:

Применим это разложение для эквиваленции:

таким образом,

Для булевой функции n переменных справедливо тождество:

Применяя это выражение многократно для всех х_i (i = 1,2,..., n), получим:

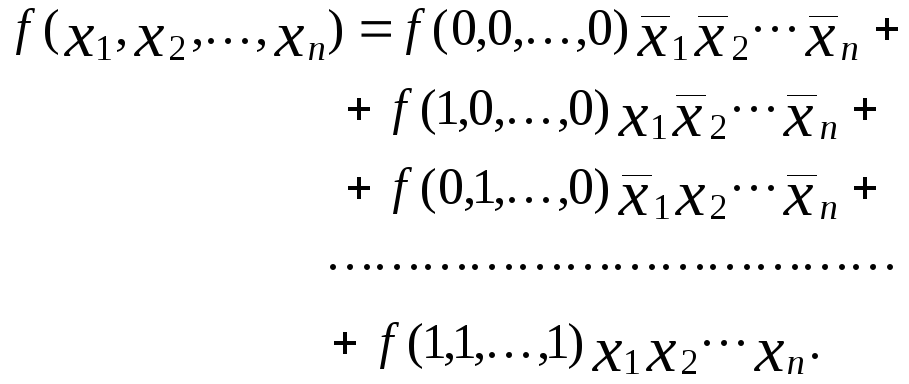(2)

В выражении (2) слагаемые, для которых f(...) = 0, можно опустить. Дизъюнкция оставшихся конъюнкций называется совершенной дизъюнктивной нормальной формой - СДНФ. Ее совершенство заключается в однородности состава всех конъюнкций, в каждую из которых входит полный набор n аргументов. Формула (1) является примером несовершенной ДНФ, так как в каждое слагаемое входит только по одному аргументу. СДНФ (2) генерируется по таблице истинности следующим образом. Суммируются конъюнкции на наборах-строчках с ненулевым значением f(...) = 1, при этом единичному значению i-го аргумента в данной строке соответствует сомножитель х_i , нулевому значению - его отрицание В качестве примера приведем к СДНФ импликацию, заданную таблицей, справа от которой выписаны слагаемые на единичных наборах (табл. 5). Ее СДНФравна

.

Упрощение СДНФ приводит к более простой ДНФ:

Дальнейшие упрощения дают правую часть (1):

Таблица 5			Таблица 6
x y	x®y		x1 x2 x3	f(x1, x2, x3)
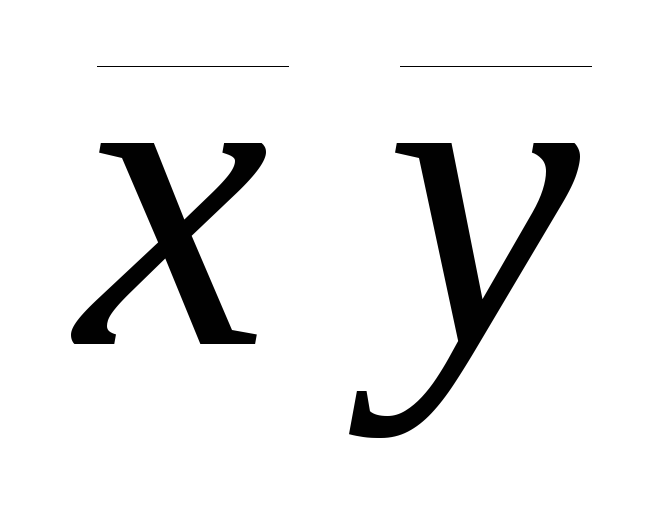
0 0	1		0 0 0	0	x1 + x2 + x3
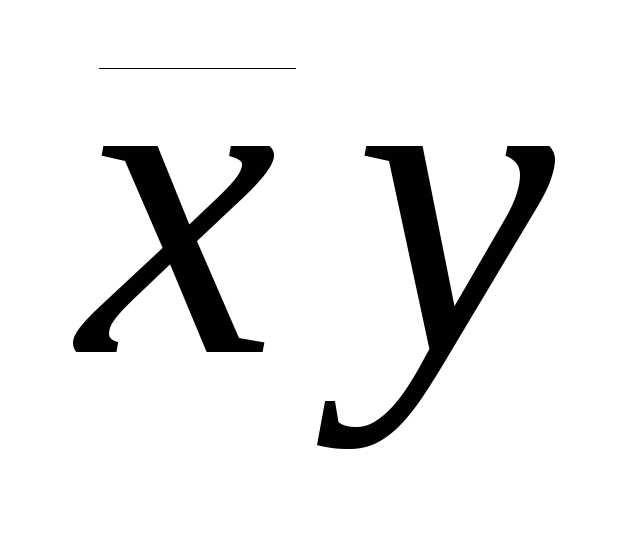
0 1	1		0 0 1	1
1 0	0		0 1 0	0
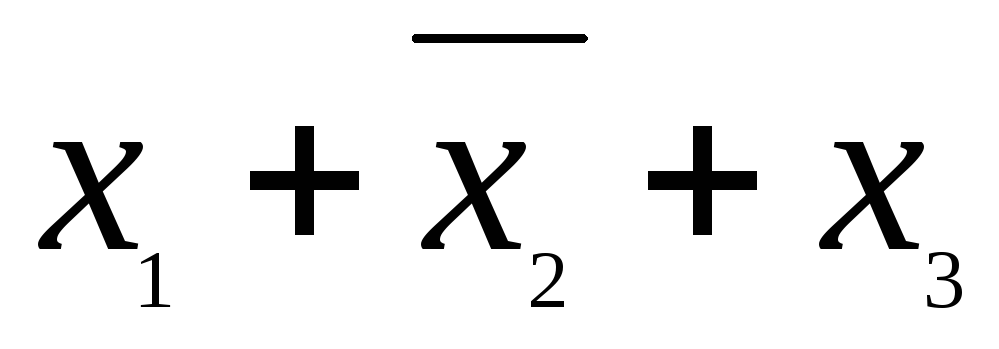
1 1	1	x y	0 1 1	0
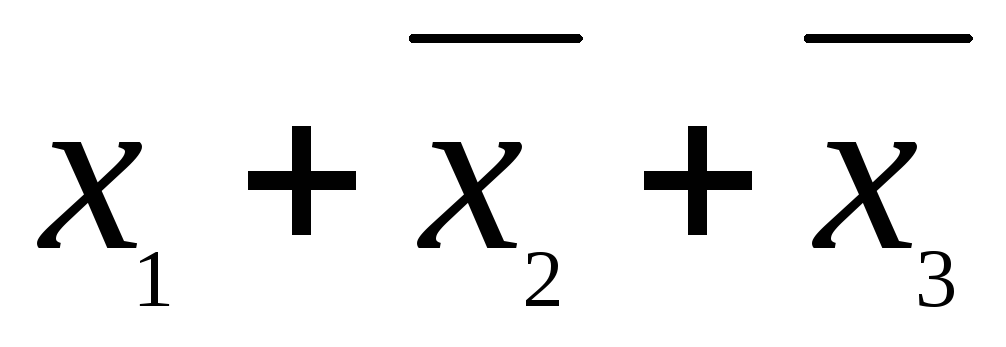
			1 0 0	1
			1 0 1	1
			1 1 0	0
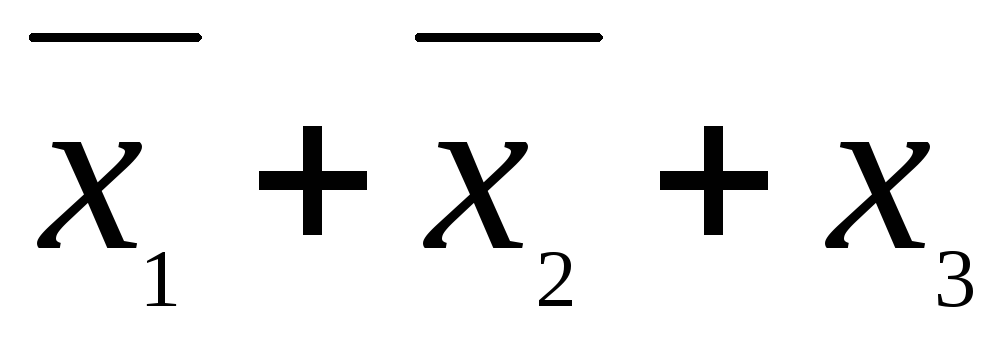
			1 1 1	1

Применение законов двойственности к СДНФ позволяет получить представление произвольной булевой функции в виде конъюнкции дизъюнкций - совершенной конъюнктивной нормальной формы (СКНФ). Теперь по таблице истинности выбираются строчки, соответствующие наборам с нулевым значением f(...)=0. Для каждой из них составляется дизъюнкция аргументов, либо их отрицаний (в случае x_i = 1).

Построим СКНФ для функции, представленной таблицей 6. Cправа от строк, где f(...)=0, выписаны соответствующие дизъюнкции. СКНФ имеет вид:

.

Алгебра высказываний является эффективным аппаратом проектирования цифровых схем, состоящих из двоичных логических элементов. Рассмотрим электрические схемы из проводников и переключателей (рис. 3.1,а).

Единственные фрагменты, которыми схемы отличаются друг от друга - это их нижние части, содержащие переключатели. Следовательно, остальные части схем можно не изображать (см. релейно-контактные схемы на рис. 3.1,b).

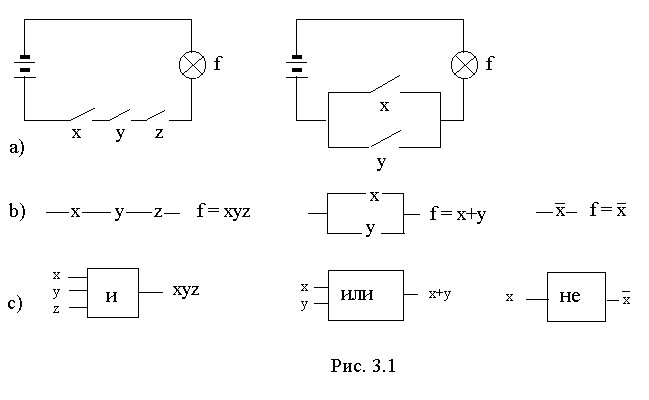
Элементы современных микросхем (рис. 3.1,c) принято называть вентилями И (реализация конъюнкции), ИЛИ (реализация дизъюнкции), НЕ (реализация отрицания – инвертор).

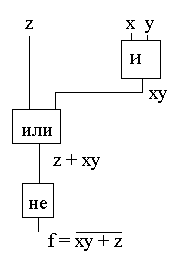
Анализ вентильной схемы заключается в нахождении булевой функции f(x₁,...,x_n), которую она реализует, и ее таблицы истинности:

	x y z	0 0 0 0 1 1 1 1 0 0 1 1 0 0 1 1 0 1 0 1 0 1 0 1
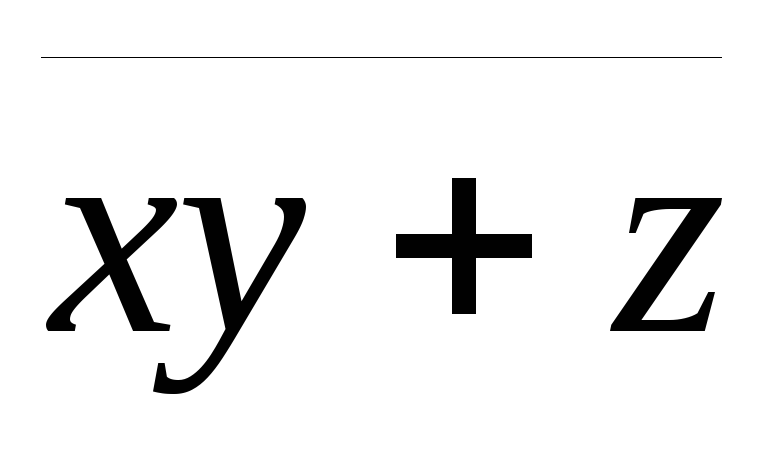
	xy xy + z	0 0 0 0 0 0 1 1 0 1 0 1 0 1 1 1 1 0 1 0 1 0 0 0

Приведем пример обратной задачи синтеза - реализации булевой функции вентильными схемами, соответствующими СДНФ (рис. 3.2,а) и СКНФ (рис. 3.2,b). Очевидно, СКНФ дает более экономичный вариант реализации функции f.

Исчисление высказываний помогает решить задачу оптимального синтеза - упрощения схемы посредством минимизации логических выражений на основе законов булевой алгебры, например:

X Y z	F		Рис. 3.2
0 0 0 0 0 1 0 1 0 0 1 1 1 0 0 1 0 1 1 1 0 1 1 1	0 1 0 1 0 1 1 1	x+y+z
СДНФ: СКНФ:

Упростим СДНФ предыдущей функции:

Оптимальная цифровая схема для данной функции реализуется двумя вентилями:

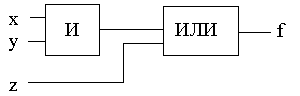
Логические схемы, имеющие множество выходов, описываются системой булевых функций:

Y₁ = f(X₁, X₂,..., X_n),

Y₂ = f(X₁, X₂,..., X_n),

-----------------------

Y_m = f(X₁, X₂,..., X_n).

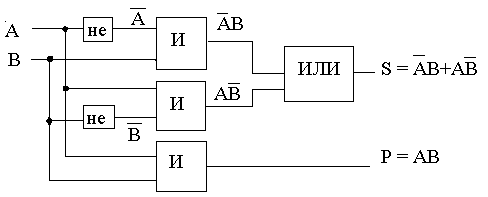
В качестве примера рассмотрим схему полусумматора, реализующего суммирование одного разряда двоичных чисел в соответствии с таблицей:

вход	выход
A B	S P
0 0 0 1 1 0 1 1	0 0 1 0 1 0 0 1

Результат суммирования S становится 1 только при комбинациях (0,1) и (1,0), то есть, ПереносP в следующий разряд имеет место только при (1,1), поэтому P = AB.