Алгебра множеств Операция объединения множеств.

Объединение множеств – множество, состоящее из всех тех и только тех элементов, которые принадлежат хотя бы одному из объединяемых множеств

Объединение множеств X и Y обозначается через .

Формальное определение

={x│xX или xY }.

Примеры:

1) Если Х={1,2,3,4,5} и Y= {2,4,6,7}, то = {1,2,3,4,5,6,7}.

2) Если X – множество отличников в группе, Y – мно­жество студентов, проживающих в общежитии, то – множество студентов, которые или учатся на отлично, или проживают в общежитии.

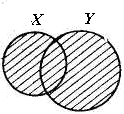
Объединение двух множеств можно пояснить рис. 1 с использованием диаграмм.
Рис. 1	Если X – множество точек левого круга, Y – множество точек правого круга, то представляет собой заштрихованную область, ограниченную обоими кругами.

Понятие объединения можно распространить и на большее число множеств.

Для операции объединения множеств справедливы коммутативный и ассоциативный законы:

= и =)=,

справедливость которых вытекает из того, что левая и правая части равенств состоят из одних и тех же элементов.

Кроме того, =. Это также очевидное соотношение, так как пустое множество не содержит элементов, а значит, и состоят из одних и тех же элементов. Таким образом, в алгебре множеств пустое множество при выполнении операции объединения множеств играет роль нуля. Здесь имеет место аналогия с выражением а+0=а в обычной алгебре.

В отличие от этого, выполнение операции объединения любого множества с универсальным множеством не имеет аналогии в обычной алгебре: для любого множества X справедливо соотношение ХI=I (в то время как в обычной алгебре а+1= а1).

Действительно, объединение ХI представляет собой универсальное множество I, включающее все элементы множест­ва X в качестве своего подмножества.

Операция пересечения множеств.

Пересечение множеств – множество, состоящее из всех тех и только тех элементов, которые принадлежат каждому из объединяемых множеств.

Пересечение множеств X и Y обозначается через XY.

Формальное определение

={x│xX и xY }.

Пересечение множеств иногда называют произведением множеств и обозначают XY. Однако свойства пересечения множеств несколько отличаются от свойств произведения в обычном арифметическом понимании, поэтому этим термином мы пользоваться не будем.

Примеры:

1) Если Х={1,2,3,4,5} и Y= {2,4,6,7}, то = {2,4}.

2) Если X – множество отличников в группе, Y – мно­жество отличников группы, проживающих в общежитии.

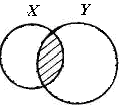
Рис. 2

3) Пересечение двух множеств можно пояснить рис. 2 с использованием диаграмм: представляет собой заштрихованную область, являющуюся общей частью обоих кругов.

Множества X и Y называют непересекающимися, если они не имеют общих элементов, т. е. если =0.

Примеры непересекающихся множеств:

1. множества {1, 2, 3} и {4, 5, 6};

2. множество отличников и множество неуспевающих студентов в группе;

3. множества точек кругов, не имеющих общих точек.

Объединение и пересечение множеств иногда называют суммой множеств и обозначают соответственно X+Y и XY. Однако свойства объединения множеств несколько отличаются от свойств суммы и произведения при обычном арифметическом понимании, поэтому терминами «сумма» и «произведение» применительно к множествам далее использованы не будут.

Понятие пересечения можно распространить и на боль­шее, чем два, число множеств.

Для операции пересечения множеств справедливы коммутатив­ный и ассоциативный законы:

= и =)=.

Кроме того, = и I=X, то есть пустое и универсальное множества при выполнении операции пересечения играют в алгебре множеств роль нуля и единицы соотвественно. Здесь имеет место аналогия с выражениями а·0=0 и а·1=а в обычной алгебре.