10 Плоскости, касательные к кривым поверхностям.

На кривой поверхности ω через точку А (рис. 68 ) проведем несколько кривых линий m,l… и к этим кривым проведем касательные прямые b,c… Совокупность этих касательных прямых в зависимости от расположения точки А на кривой поверхности образуют или касательную плоскость α или коническую поверхность.

Если через точку А можно провести плоскость, то эту точку называют обыкновенной. Если же касательные прямые b,с…образуют коническую поверхность, то точку А называют конической. Таким образом, плоскость, касательная к поверхности в данной на ней обыкновенной точке, является геометрическим местом прямых, проведенных через данную точку, и касательных к кривым линиям, проходящим на поверхности через эту же точку.

Рис. 68

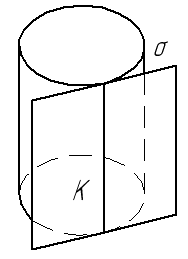
Если же поверхность линейчатая, то через данную точку(К) можно провести прямолинейную образующую. Следовательно, плоскость касается линейчатой поверхности по прямой линии ( рис. 69). Некоторых поверхностей плоскость может касаться по кривой линии. Так, например, если провести касательную плоскость к наружной части кольца, образованного движением замкнутой кривой (окружности) по некоторой плоскости кривой, то плоскость будет касаться этого кольца по кривой линии.

Рис. 69

Д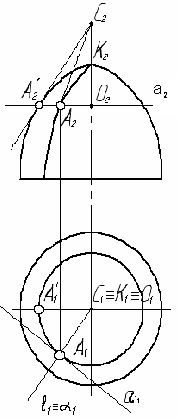ля построения касательной плоскости в обыкновенной точке поверхности достаточно через эту точку провести две касательные прямые к двум кривым на этой поверхности, проходящим через данную точку.

Пример 1. Через точку А поверхности вращения проведем касательную плоскость ( рис. 70 ).

Для этого через точку А на поверхности проводим окружность с центром О, плоскость которой(β) перпендикулярна к оси вращения, и меридиана l. Горизонтальная проекция l₁ меридиана совпадает с горизонтальной проекцией плоскости α₁ меридиана. Если в точке А к указанным окружности и меридиану провести касательные прямые, то они определяют плоскость, касательную к данной поверхности вращения.

Горизонтальная проекция прямой а ,касательной к окружности в точке А , изображается прямой а₁, касательной к горизонтальной проекции этой окружности в точке А₁, а фронтальная проекция прямой а₂ совпадает с фронтальной проекцией окружности, представляющей горизонтальную прямую.

Для построения прямой АС , касательной к меридиану в точке А, повернем плоскость α меридиана в положение, параллельное плоскости П₂, т.е. данный меридиан совместим с главным. Рис. 70

Тогда точка А₂ займет положение точки А’₂. В новом положении меридиана проведем фронтальную проекцию А’₂С₂, касательную к меридиану. Обратным вращением меридиан вместе с касательной АС возвращаем в первоначальное положение. Так как точка С, лежащая на оси вращения не перемещается, то легко построить проекцииА₂С₂ и А₁С₁ прямой, касательной к меридиану. Прямые АС и а определяют плоскость, касающуюся данной поверхности в точке А.

П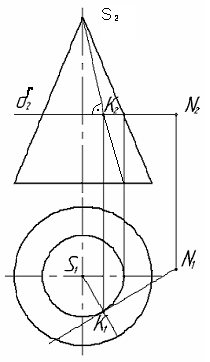ример 2. Построить плоскость, касательную к конусу вращения и проходящую через точку N, заданную вне его поверхности ( рис. 71 ).

Через точку N проведем плоскость δ₂ , перпендикулярную к оси вращения. Окружность, полученную при пересечении конуса плоскостью δ, принимаем за одну из кривых поверхности конуса. К ней проведем касательную NK.

Образующая SK конуса, проходящая через точку К , совместно с прямой NK определяет касательную плоскость к поверхности конуса.

Пример 3. Построить плоскость,

касательную к цилиндру и параллельную

данной прямой l ( рис. 72 ).

На прямой l возьмем произвольную точку

А и проведем прямую АМ, параллельную образующим

цилиндра. Пересекающиеся прямые l и АМ определяют плоскость δ, параллельную образующим цилиндра.

Построим линию МN пересечения плоскости δ с плоскостью ω нижнего основания цилиндра. Для этого определим точки встречи M и N прямых АМ и l с плоскостью ω. Фронтальная проекция M₂N₂ прямой MN совпадает с плоскостью ω₂ , а горизонтальная Рис. 71

M₁N₁ является горизонтальным следом плоскости δ.

В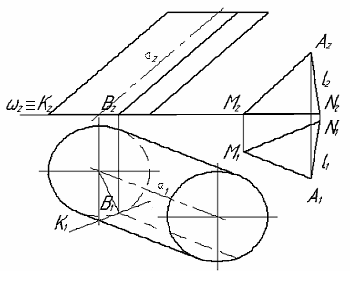плоскости ω проводим прямуюк, касательную к нижнему основанию цилиндра в точке В и параллельную прямой MN. Прямая к и образующая а, проходящая через точку В касания, определяет искомую плоскость.

Рис. 72