
- •30 AnGeom
- •2. Прямая линия на плоскости
- •Типы уравнений прямой.
- •3. Угол между двумя прямыми. Условие параллельности и перпендикулярности.
- •Линейные образы в r3
- •4. Понятие алгебраической поверхности.
- •4.А. Плоскость.
- •5. Прямая линия в пространстве.
- •5.А. Канонические уравнения прямой в пространстве.
- •5.Б. Приведение общих уравнений прямой к каноническому виду.
- •6. Угол между двумя прямыми. За угол между двумя прямыми
- •7. Прямая и плоскость.
- •Условие того, что прямая лежит в данной плоскости.
- •Условие того, что две прямые лежат в одной плоскости.
- •8. Кривые второго порядка.
- •8.А Окружность
- •8.Б. Эллипс (в декартовой системе координат)
- •8.В. Гипербола
- •Каноническое уравнение гиперболы
- •8.Г. Парабола
- •Пример 18. Установить, что уравнение
- •Полярная система координат.
- •Связь между прямоугольными и полярными координатами.
8.В. Гипербола
Г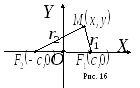 иперболой
называется множество точек плоскости,
разность расстояний которых до двух
данных точек, называемых фокусами
гиперболы, постоянна и равна
иперболой
называется множество точек плоскости,
разность расстояний которых до двух
данных точек, называемых фокусами
гиперболы, постоянна и равна![]() (рис. 16).
(рис. 16).
Фокальная
ось гиперболы
![]() ;
;![]() ,
– фокальные радиусы гиперболы,
,
– фокальные радиусы гиперболы,
соответствующие
точке
![]() .
.![]() ;
;![]() ,
,![]() (
по свойству сторон треугольника).
(
по свойству сторон треугольника).
Каноническое уравнение гиперболы
![]() .
.
Обозначим
![]() ,
тогда уравнение гиперболы примет вид:
,
тогда уравнение гиперболы примет вид:
![]()
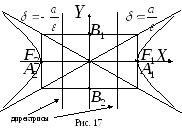 .
(34)
.
(34)
Вершины
гиперболы:
![]() – вещественные вершины;
– вещественные вершины;![]() – мнимые вершины.
– мнимые вершины.
Прямые
![]() являются асимптотами гиперболы (рис.
17).
являются асимптотами гиперболы (рис.
17).
Гипербола
состоит из двух несмыкающихся ветвей,
лежащих в углах между прямыми
![]() ,
,![]() и неограниченно приближающихся к этим
прямым.
и неограниченно приближающихся к этим
прямым.![]() вещественная ось,
вещественная ось,![]() – мнимая ось.
– мнимая ось.
Эксцентриситет
гиперболы
![]() .
.
Директрисы гиперболы обладают тем свойством, что отношение расстояния любой точки гиперболы до фокуса к расстоянию до соответствующей директрисы есть величина постоянная, равная эксцентриситету гиперболы.
Уравнение
директрис
![]() или
или![]() .
.
8.Г. Парабола
П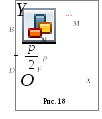 араболой
называется множество точек плоскости,
одинаково удаленных от заданной прямой
(директрисы) и заданной точки (фокуса).
Пусть точка
араболой
называется множество точек плоскости,
одинаково удаленных от заданной прямой
(директрисы) и заданной точки (фокуса).
Пусть точка
![]() – фокус. Прямая
– фокус. Прямая![]() – директриса параболы;
– директриса параболы;![]() – произвольная точка параболы,
– произвольная точка параболы,![]() параметр параболы.
параметр параболы.
По
определению параболы
![]() .
Уравнение параболы с вершиной в точке
.
Уравнение параболы с вершиной в точке![]() и директрисой
и директрисой![]() (см. рис. 18) , заданной уравнением
(см. рис. 18) , заданной уравнением![]() ,
имеет канонический вид:
,
имеет канонический вид:
![]() .
(35)
.
(35)
З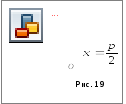 амечание:
если положить
амечание:
если положить![]() ,
то
,
то![]() ,
то есть
,
то есть![]() (
(![]() ).
Эксцентриситет параболы
= 1.
).
Эксцентриситет параболы
= 1.
Другие виды параболы:
2)
![]() (рис. 19) - парабола с осью симметрии
(рис. 19) - парабола с осью симметрии![]() ,
фокусом
,
фокусом![]() и директрисой
и директрисой![]() .
.
3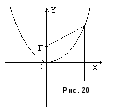 )
)![]() - (рис. 20.) парабола с осью симметрии
- (рис. 20.) парабола с осью симметрии![]() ,
фокусом
,
фокусом![]() и директрисой
и директрисой![]() .
.
4)
![]() - (рис. 21.) парабола с осью симметрии
- (рис. 21.) парабола с осью симметрии![]() ,
фокусом
,
фокусом![]() и директрисой
и директрисой![]() .
.
Пример 18. Установить, что уравнение
![]()
определяет
эллипс. Найти его центр
![]() ,
полуоси, координаты фокусов
,
полуоси, координаты фокусов![]() ,
,![]() ,
эксцентриситет и уравнения директрис.
Сделать чертеж.
,
эксцентриситет и уравнения директрис.
Сделать чертеж.
Решение.
1. В заданном уравнении сгруппируем слагаемые, содержащие одноименные координаты и вынесем коэффициенты при квадратах за скобки:
![]() .
.
Дополним выражения, стоящие в скобках, до полного квадрата и полученные свободные константы перенесем в правую часть:
![]() ,
,
![]() ,
,
![]() .
.
Разделим обе части уравнения на 45, получим
![]() .
.
2.
Введем новую систему координат
![]() ,
полученную сдвигом по каждой из
координатных осей, и связанную со старой
декартовой системой координат равенствами:
,
полученную сдвигом по каждой из
координатных осей, и связанную со старой
декартовой системой координат равенствами:
 (1).
(1).
Тогда, исследуемое уравнение кривой относительно новых осей примет вид:
![]() ,
,
![]() .
.
Это
есть канонический вид эллипса с центром
![]() ,
большой полуосью
,
большой полуосью![]() ,
малой полуосью
,
малой полуосью![]() .
Фокусы эллипса располагаются на оси
.
Фокусы эллипса располагаются на оси![]() на расстоянии
на расстоянии![]() от начала координат
от начала координат![]() ,
в точках
,
в точках![]() ,
,![]() в новой системе координатXOY.
в новой системе координатXOY.
Вычисляем,
![]() ,
,![]() ,
,![]() .
Мера сжатия, то есть эксцентриситет,
дается равенством
.
Мера сжатия, то есть эксцентриситет,
дается равенством![]() .
Отсюда
.
Отсюда![]() .
Директрисы эллипса в системеXOY
задаются уравнениями
.
Директрисы эллипса в системеXOY
задаются уравнениями
![]() .
В нашем случае,
.
В нашем случае,![]() .
.
3. Чтобы
найти координаты центра и фокусов в
старой системе
![]() ,
воспользуемся равенствами (1),
осуществляющими связь систем координат:
,
воспользуемся равенствами (1),
осуществляющими связь систем координат:
центр
![]() :
:
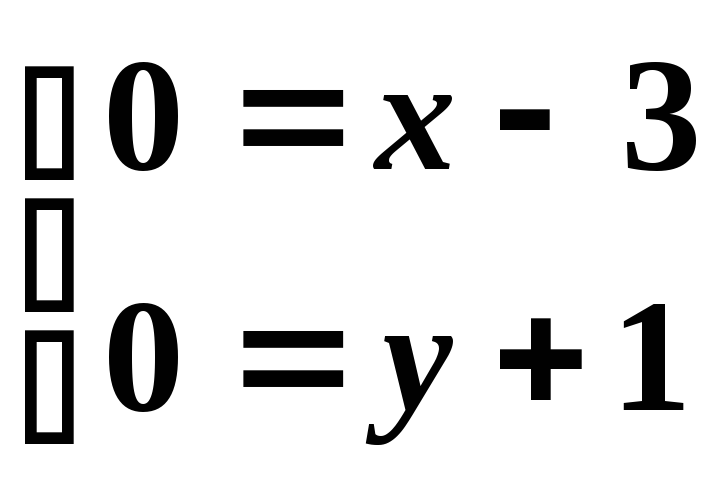 ,
,
![]() ,
,
фокусы
![]() :
:
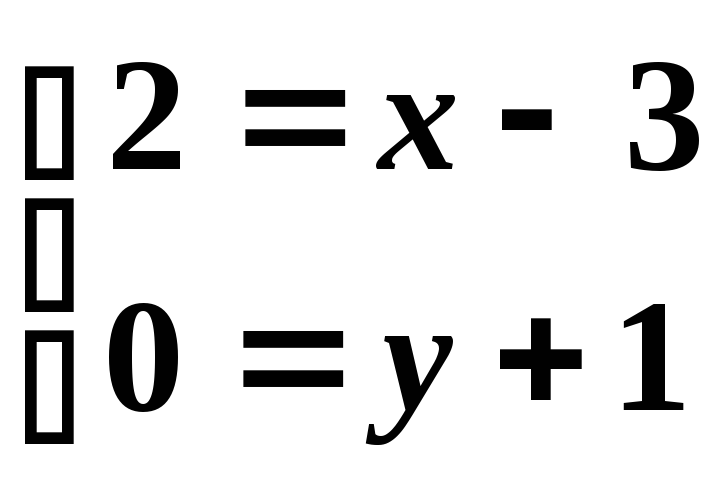 ,
,
![]() ,
,
![]() :
:
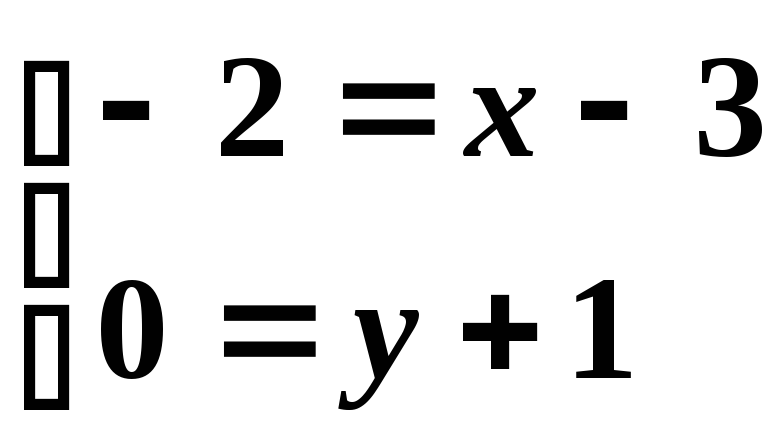 ,
,
![]() .
.
Уравнения
директрис:
![]() .
.
4. Теперь
построим эллипс. С помощью параллельного
переноса системы координат
![]() образуем новую систему координат
образуем новую систему координат![]() так, чтобы новое начало координат
так, чтобы новое начало координат![]() совпадало с точкой
совпадало с точкой![]() .
При указанном выборе, оси координат
системы
.
При указанном выборе, оси координат
системы![]() являются осями симметрии эллипса, а
точка
являются осями симметрии эллипса, а
точка![]() - центром симметрии. Теперь симметрично
- центром симметрии. Теперь симметрично![]() по оси
по оси![]() отложим о
отложим о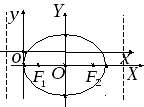 трезки
длины
трезки
длины![]() ,
а по оси
,
а по оси![]() отрезки длины
отрезки длины![]() .
.
Соединив
найденные вершины, получим эллипс. На
оси
![]() симметрично относительно
симметрично относительно![]() на расстоянии
на расстоянии![]() отложим точки
отложим точки![]() ,
,![]() - фокусы эллипса. Так как директрисы
эллипса описываются уравнениями
- фокусы эллипса. Так как директрисы
эллипса описываются уравнениями![]() ,
то они располагаются параллельно
,
то они располагаются параллельно
![]() ,
причем одна из них проходит через точку
,
причем одна из них проходит через точку
![]() ,
другая через
,
другая через![]() .
.
Остальные примеры в другом файле.
