
- •30 AnGeom
- •2. Прямая линия на плоскости
- •Типы уравнений прямой.
- •3. Угол между двумя прямыми. Условие параллельности и перпендикулярности.
- •Линейные образы в r3
- •4. Понятие алгебраической поверхности.
- •4.А. Плоскость.
- •5. Прямая линия в пространстве.
- •5.А. Канонические уравнения прямой в пространстве.
- •5.Б. Приведение общих уравнений прямой к каноническому виду.
- •6. Угол между двумя прямыми. За угол между двумя прямыми
- •7. Прямая и плоскость.
- •Условие того, что прямая лежит в данной плоскости.
- •Условие того, что две прямые лежат в одной плоскости.
- •8. Кривые второго порядка.
- •8.А Окружность
- •8.Б. Эллипс (в декартовой системе координат)
- •8.В. Гипербола
- •Каноническое уравнение гиперболы
- •8.Г. Парабола
- •Пример 18. Установить, что уравнение
- •Полярная система координат.
- •Связь между прямоугольными и полярными координатами.
Типы уравнений прямой.
Название уравнения определяется названием постоянных величин, определяющих положение прямой линии в системе координат.
Уравнение прямой линии, проходящей через данную точку
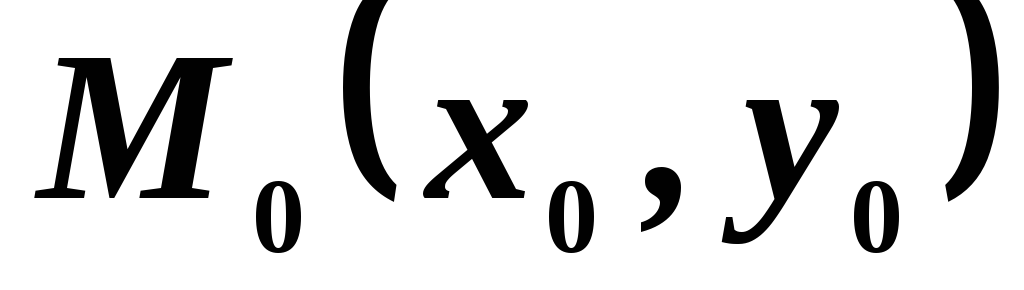 ,
перпендикулярно данному вектору
,
перпендикулярно данному вектору
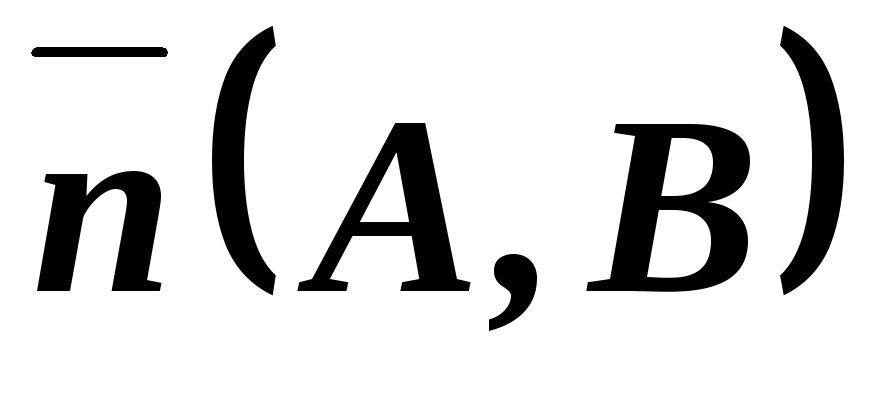 имеет вид:
имеет вид:
![]() (1)
(1)
Оно вытекает из условия того, что скалярное произведение взаимно перпендикулярных векторов равно нулю.
Действительно,
возьмем на прямой произвольную точку
![]() .
Образуем текущий вектор
.
Образуем текущий вектор![]() ,
направленный из точки
,
направленный из точки![]() в точку
в точку![]() .
Этот вектор будет иметь координаты
.
Этот вектор будет иметь координаты![]() ,
и направлен он будет вдоль прямой. Второй
вектор – это данный вектор
,
и направлен он будет вдоль прямой. Второй
вектор – это данный вектор![]() .
Скалярное произведение этих векторов
равно нулю, отсюда и вытекает уравнение
прямой.
.
Скалярное произведение этих векторов
равно нулю, отсюда и вытекает уравнение
прямой.
Общее уравнение прямой линии:
![]() (2)
(2)
где
коэффициенты при неизвестных
![]() суть координаты нормального вектора
прямой. Действительно, раскроем скобки
в предыдущем уравнении:
суть координаты нормального вектора
прямой. Действительно, раскроем скобки
в предыдущем уравнении:
![]()
Теорема 1. Всякая прямая на плоскости имеет уравнение первой степени, и всякое уравнение первой степени является уравнением некоторой прямой.
Следствия.
a)
![]() – уравнение прямой, параллельной оси
– уравнение прямой, параллельной оси![]() (
(![]() ,
уравнение оси
,
уравнение оси![]() ),
),
б)
![]() - уравнение прямой, параллельной оси
- уравнение прямой, параллельной оси![]() (
(![]() ,
уравнение оси
,
уравнение оси![]() ),
),
в)
![]() - прямая линия, проходящая через начало
координат.
- прямая линия, проходящая через начало
координат.
Замечание.
При переменном коэффициенте
![]() - это будут уравнения пучка прямых,
проходящих через начало координат.
- это будут уравнения пучка прямых,
проходящих через начало координат.
Уравнение прямой линии, проходящей через данную точку
 ,
параллельно данному вектору
,
параллельно данному вектору (каноническое):
(каноническое):
![]() (3)
(3)
Вектор
вдоль прямой
![]() коллинеарен вектору
коллинеарен вектору![]() ,
отсюда это условие.
,
отсюда это условие.
Уравнение прямой, проходящей через данную точку в заданном направлении:
![]() (4)
(4)
З амечание.
При переменном коэффициенте
амечание.
При переменном коэффициенте![]() уравнение называется уравнением пучка
прямых линий, проходящих через точку
уравнение называется уравнением пучка
прямых линий, проходящих через точку![]() .
.
Уравнение прямой линии с угловым коэффициентом (рис. 4):
![]() (5)
(5)
Здесь
![]()
![]() .
К этому виду нельзя привести прямую,
параллельную оси
.
К этому виду нельзя привести прямую,
параллельную оси
![]() .
.
Уравнение прямой, проходящей через две данные точки:
![]() (6)
(6)
Действительно,
пусть даны две точки
![]() и
и![]() ,
через которые должна пройти наша прямая.
На этой прямой возьмем текущую точку
,
через которые должна пройти наша прямая.
На этой прямой возьмем текущую точку![]() и образуем два вектора:
и образуем два вектора:![]() и
и![]() .
Эти два вектора коллинеарные, отсюда и
вытекает уравнение.
.
Эти два вектора коллинеарные, отсюда и
вытекает уравнение.
Замечание.
Если
![]() ,
то
уравнение прямой
,
то
уравнение прямой
![]() ;
если
;
если![]() ,
то
,
то![]() .
.
3. Угол между двумя прямыми. Условие параллельности и перпендикулярности.
1) Пусть прямые линии заданы общими уравнениями:
![]()
![]() ,
,
где
нормальные векторы:
![]() и
и
![]() 2,
2,
![]() - угол между векторами
- угол между векторами![]() и
и
![]() ,
т.е. угол между прямыми. Тогда:
,
т.е. угол между прямыми. Тогда:
![]() (7)
(7)
Условие параллельности прямых эквивалентно условию коллинеарности их нормальных векторов:
![]() (8)
(8)
Условие
перпендикулярности прямых – ортогональность
векторов
![]() и
и![]() :
:
![]() (9)
(9)
2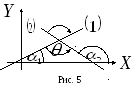 ) Пусть
прямые линии заданы с угловыми
коэффициентами
) Пусть
прямые линии заданы с угловыми
коэффициентами![]() (рис.
5):
(рис.
5):![]() ,
,
где
![]()
![]() .
Тогда
.
Тогда
![]() .
.
Это
вытекает из формулы тангенса суммы
углов.
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() (*).
(*).
За
![]() принимаем угловой коэффициент той
прямой, которую надо вращать против
хода часовой стрелки, чтобы обойти угол
принимаем угловой коэффициент той
прямой, которую надо вращать против
хода часовой стрелки, чтобы обойти угол![]() до совмещения со второй прямой.
до совмещения со второй прямой.
Условие
параллельности прямых:
![]() .
.
Условие
перпендикулярности прямых:
![]() .
.
Расстояние
точки
![]() от прямой
от прямой![]() определяется формулой:
определяется формулой:
![]() (10)
(10)
Доказательство смотри в другом файле.
Замечания.
1.
Если две прямые
![]() и
и![]() заданы в каноническом виде, то угол
между ними можно рассматривать как угол
между их направляющими векторами
заданы в каноническом виде, то угол
между ними можно рассматривать как угол
между их направляющими векторами![]() ,
а значит,
,
а значит,
![]() (11)
(11)
Пример
1.
Даны
точки
![]() ,
,![]() ,
,![]() .
.
Найти:
1)
Уравнение прямой
![]() .
.
Согласно уравнению (6) (уравнение прямой, проходящей через две точки), запишем:
![]() ,
или
,
или
![]() .
.
2)
Уравнение прямой
![]() ,
проходящей через точку
,
проходящей через точку![]() ,
параллельно прямой
,
параллельно прямой![]() .
.
Согласно
уравнению (1), (уравнение прямой, проходящей
через точку параллельно данному вектору)
точка
![]() это точка
это точка![]() ,
параллельно прямой
,
параллельно прямой![]() значит перпендикулярно ее нормальному
вектору
значит перпендикулярно ее нормальному
вектору![]() .
Следовательно, запишем
.
Следовательно, запишем
![]() .
.
3) Уравнение
прямой
![]() ,
проходящей через точку
,
проходящей через точку![]() ,
перпендикулярно прямой
,
перпендикулярно прямой![]() .
.
Перпендикулярно
прямой, значит параллельно ее нормальному
вектору, в нашем случае
![]() . Точка
. Точка![]() это точка
это точка![]() .
Согласно уравнению (3), запишем
.
Согласно уравнению (3), запишем
![]()
4)
Уравнение медианы
![]() треугольника
треугольника![]() .
.
На
медиане
![]() образуем текущий вектор
образуем текущий вектор![]() .
.
Найдем
координаты точки
![]() - середины стороны
- середины стороны![]() :
:
![]()
Образуем
вектор
![]() ,
расположенный параллельно текущему
вектору
,
расположенный параллельно текущему
вектору![]() .
Тогда, в силу условия параллельности
векторов, получим уравнение медианы
.
Тогда, в силу условия параллельности
векторов, получим уравнение медианы![]() :
:
![]() ,
или
,
или
![]() .
.
5)
Уравнение высоты
![]() .
.
На
высоте
![]() возьмем текущую точку
возьмем текущую точку![]() и образуем текущий вектор
и образуем текущий вектор![]() .
Так как
.
Так как![]()
![]() ,
где
,
где![]() ,
то условие перпендикулярности этих
векторов порождает уравнение прямой
,
то условие перпендикулярности этих
векторов порождает уравнение прямой![]() (скалярное произведение векторов равно
нулю):
(скалярное произведение векторов равно
нулю):
![]() или
или
![]() .
.
6)
Длину высоты
![]() .
.
Заметим,
что длина высоты
![]() равна расстоянию от точки
равна расстоянию от точки![]() до прямой
до прямой![]() .
Чтобы воспользоваться формулой (10),
сначала найдем уравнение прямой
.
Чтобы воспользоваться формулой (10),
сначала найдем уравнение прямой![]() .
.
На
стороне
![]() образуем текущий вектор
образуем текущий вектор![]() .
.
Запишем
условие параллельности векторов
![]() ,
где
,
где![]() :
:
![]() ,
или в общем виде
,
или в общем виде
![]() .
.
Теперь, подставляя известные данные в формулу (10), имеем:
![]() .
.
Пример
2. Дана
прямая
![]() :
:![]() и точка
и точка![]() .
.
Найти:
1)
Для прямой
![]() уравнение
с угловым коэффициентом, угловой
коэффициент
уравнение
с угловым коэффициентом, угловой
коэффициент
![]() ,
отрезок, отсекаемый по оси ординат.
,
отрезок, отсекаемый по оси ординат.
Разрешив
уравнение прямой
![]() относительно
относительно![]() ,
получаем уравнение с угловым коэффициентом:
,
получаем уравнение с угловым коэффициентом:
![]() :
:
![]() .
Отсюда
.
Отсюда![]() ,
,![]() .
.
Нормаль
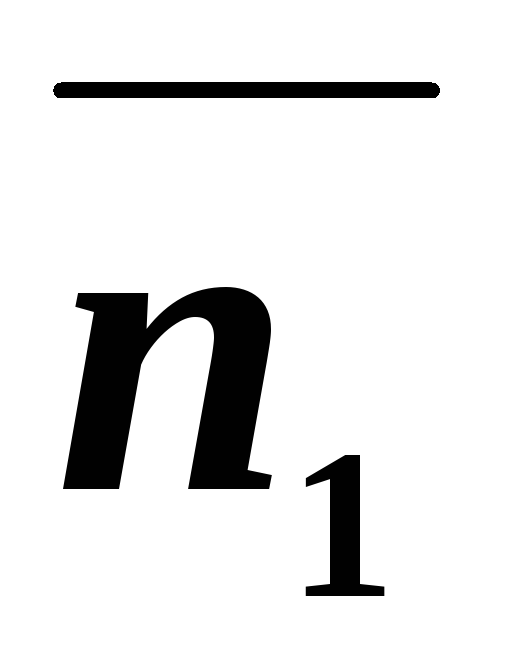 и
направляющий вектор
и
направляющий вектор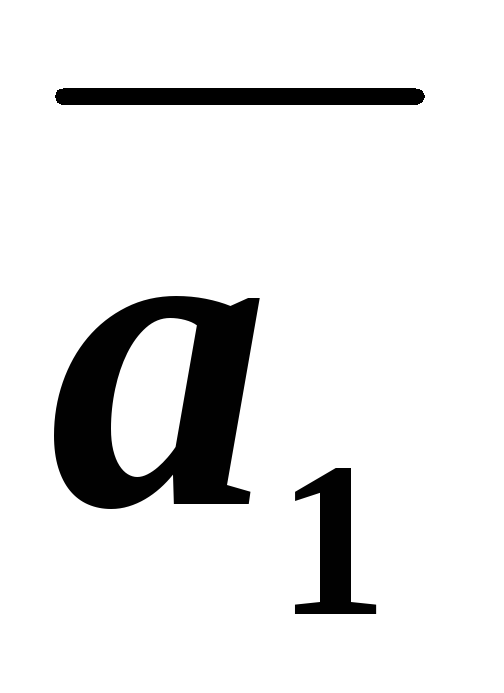 прямой
прямой -
-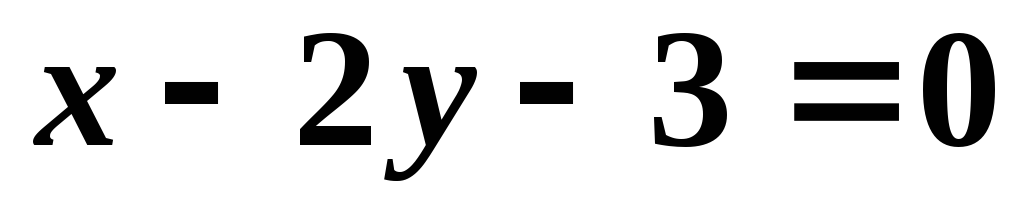 .
.
Коэффициенты
при переменных
![]() в общем уравнении прямой
в общем уравнении прямой![]() ,
есть координаты нормального вектора,
то есть
,
есть координаты нормального вектора,
то есть![]() .
.
Поскольку
направляющий вектор
![]() прямой
прямой![]() – это любой ненулевой вектор, параллельный
этой прямой, то выполняется условие
(перпендикулярность векторов):
– это любой ненулевой вектор, параллельный
этой прямой, то выполняется условие
(перпендикулярность векторов):
![]() где
где
![]() .
.
Дадим
величине
![]() какое-нибудь значение. Пусть, например,
какое-нибудь значение. Пусть, например,![]() ,
тогда
,
тогда![]() ,
то есть
,
то есть
![]() .
Получаем направляющий вектор
.
Получаем направляющий вектор
![]() .
.
Каноническое уравнение прямой
 .
.
Для
составления канонического уравнения
(3) прямой
![]() нам необходимо знать точку
нам необходимо знать точку![]() ,
лежащую на
,
лежащую на![]() ,
и направляющий вектор
,
и направляющий вектор![]() .
Так как координаты вектора
.
Так как координаты вектора![]() были получены нами ранее в задание 2,
осталось найти координаты точки
были получены нами ранее в задание 2,
осталось найти координаты точки![]() .
.
Зафиксируем
произвольное значение, например,
![]() и подставим его в уравнение прямой
и подставим его в уравнение прямой![]() .
Получим
.
Получим![]() .
Следовательно,
.
Следовательно,![]() .
.
Воспользовавшись теперь каноническим уравнением прямой (10), находим:
![]() .
.
Уравнение прямой
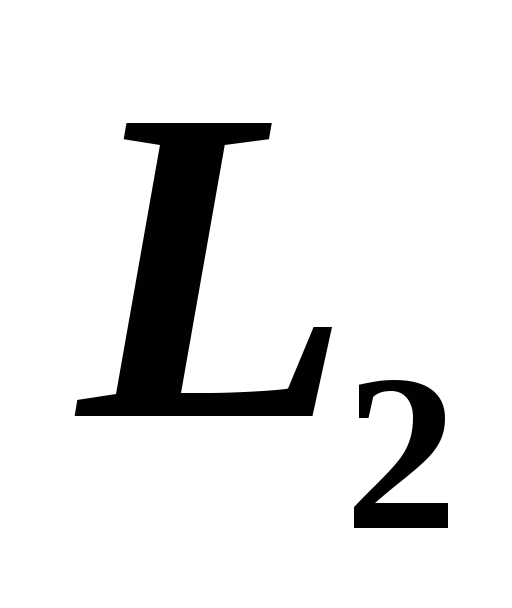 ,
параллельной
,
параллельной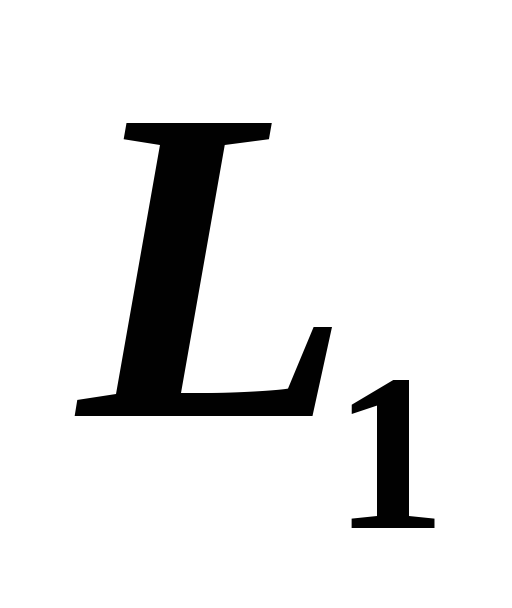 -
-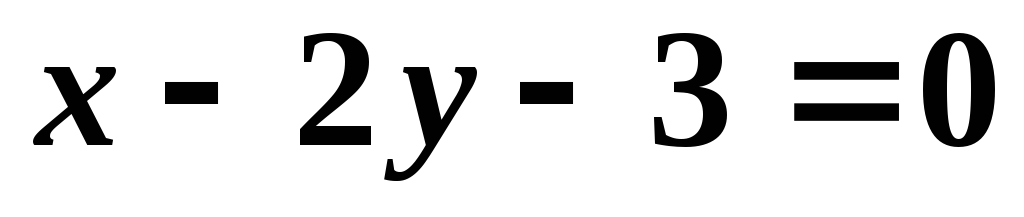 и проходящей через точку
и проходящей через точку .
.
Прежде
всего, заметим, что точка
![]() не лежит на прямой
не лежит на прямой![]() ,
поскольку ее координаты не удовлетворяют
уравнению этой прямой. Поэтому можно
построить прямую
,
поскольку ее координаты не удовлетворяют
уравнению этой прямой. Поэтому можно
построить прямую![]() ,
проходящую через
,
проходящую через![]() параллельно
параллельно![]() ,
но не совпадающую с
,
но не совпадающую с![]() .
.
Пусть
![]() - текущая точка прямой
- текущая точка прямой![]() .
Так как текущий вектор
.
Так как текущий вектор![]() перпендикулярен вектору нормали
перпендикулярен вектору нормали![]() прямой
прямой![]() ,
то
,
то![]() .
Отсюда получаем уравнение прямой
.
Отсюда получаем уравнение прямой![]() :
:
![]() или
или
![]()
уравнение прямой
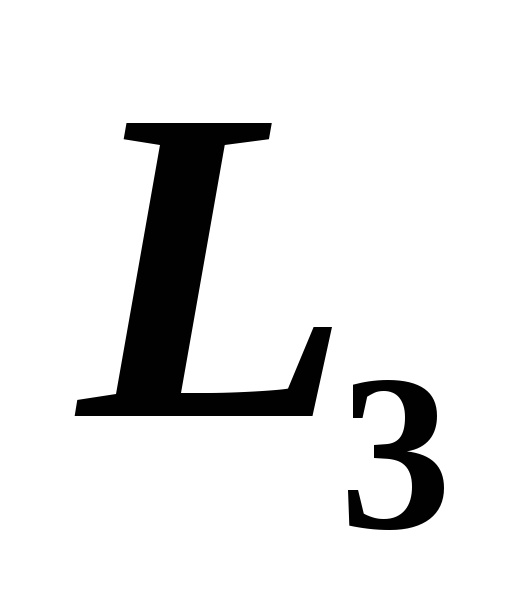 ,
перпендикулярной
,
перпендикулярной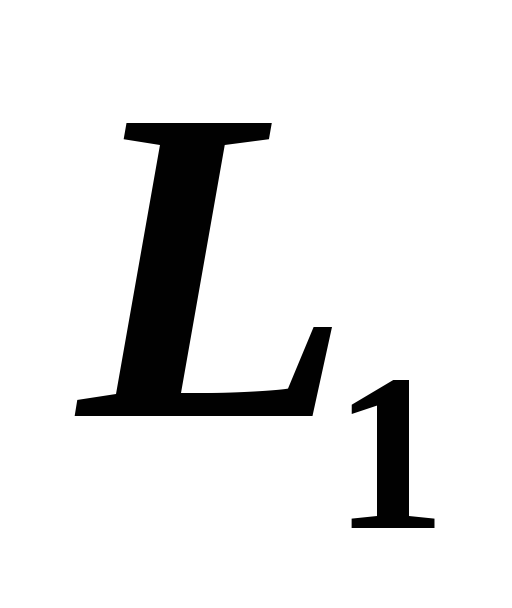 -
-
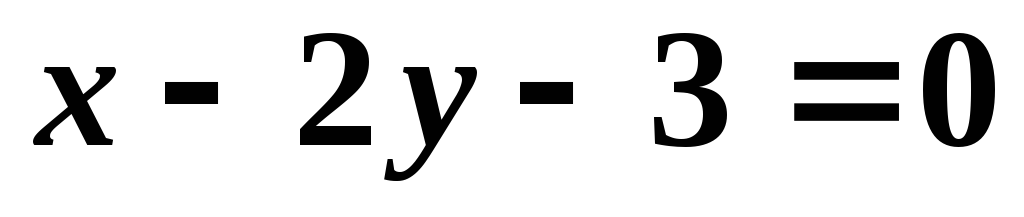 и проходящей через точку
и проходящей через точку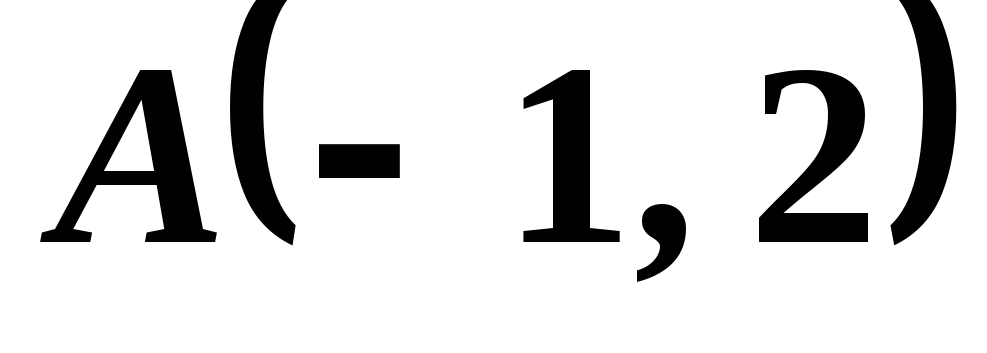 .
.
Пусть
![]() - текущий вектор прямой
- текущий вектор прямой![]() .
Из условия параллельности
.
Из условия параллельности![]() и нормали
и нормали![]() прямой
прямой![]() ,
получаем уравнение
,
получаем уравнение![]() :
:
![]() .
.
Пример 3. Проверить, являются ли прямые линии
![]() ,
,
![]()
Параллельными.
Прямые
![]() и
и![]() будут параллельны, если их нормали
будут параллельны, если их нормали![]() .
Из общего уравнения прямой
.
Из общего уравнения прямой![]() найдем нормаль
найдем нормаль![]() .
Чтобы найти нормаль
.
Чтобы найти нормаль
![]() 2
приведем уравнение прямой
2
приведем уравнение прямой
![]() к общему виду:
к общему виду:![]() .
Отсюда
.
Отсюда
![]() .
.
П![]()
![]() оскольку
условие параллельности векторов
оскольку
условие параллельности векторов![]() и
и
![]() 2
не
выполняется, так как
2
не
выполняется, так как
![]() ,
стало быть,
,
стало быть,![]() и
и
![]() не параллельны.
не параллельны.
б) Перпендикулярными.
Прямые
![]() и
и![]() будут
перпендикулярны, если
будут
перпендикулярны, если
![]()
![]()
![]() 2.
Но условие перпендикулярности для
векторов
2.
Но условие перпендикулярности для
векторов
![]() и
и
![]() 2
не
выполняется, так как
2
не
выполняется, так как
![]() .
Следовательно,
.
Следовательно,![]() не перпендикулярна
не перпендикулярна![]() .
.
в)
Найти угол
![]() между
между![]() и
и![]() .
.
Угол между прямыми равен углу между их нормалями. Поэтому, используя формулу угла между двумя векторами, получим
![]() .
.
Так
как
![]() ,
,
![]() ,
,
![]() ,
то
,
то
![]() .
.
