3. Задача классический эксперимент

1.ЦЕЛЬ РАБОТЫ

Освоить методику планирования, обработки результатов классического однофакторного эксперимента и построения на его основе обобщённых моделей.

2.ОБЩИЕ ПОЛОЖЕНИЯ

Классическим называют наиболее старый метод планирования и реализации экспериментов. Он предусматривает фиксирование на определённых уровнях всех переменных факторов, кроме одного, который принимает некоторые дискретные значения (уровни) в исследуемой части области своего существования. В результате находим зависимость исследуемой величины (параметра выхода) только от одного фактора. Математическая модель этой зависимости может быть получена в результате ряда геометрических построений или, чаще всего и с гораздо меньшей погрешностью, методом наименьших квадратов.

Поскольку этот метод не определяет структуру получаемой однофакторной модели и требует наличия перенасыщенной системы уравнений (число уравнений превышает число неизвестных) для вычисления параметров, на количество уровней переменного фактора налагаются определённые ограничения.

Если выход изменяется по закону, близкому к линейному, то для нахождения параметров линейной модели достаточно трёх точек на линии отклика. То есть достаточно варьировать переменный фактор на трёх дискретных уровнях. Однако вид линии отклика экспериментатору зачастую неизвестен. В этом случае естественное стремление сократить объём экспериментов вступает в противоречие с последующей возможностью функциональной или графической интерпретации их результатов. Последние могут подчиняться более сложному закону, (например, квадратичному) с большим числом параметров. Это обстоятельство заставляет планировать однофакторный эксперимент как минимум на четырёх уровнях переменного фактора. А при имеющейся опасности срыва одного из опытов необходимо предусмотреть пятую резервную точку.

Следует отметить, что если нелинейную экспериментальную зависимость линеаризовать логарифмированием (отложив на графике в логарифмическом масштабе), то можно для аппроксимации экспериментальных результатов использовать степенную или показательную функции.

3.ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ

3.1 Ознакомиться с содержанием методического пособия и выбрать индивидуальное задание (Табл.3).

Пример: Таблица 1.Исходные данные

Параметры		Величина
Переменные факторы	х1	50				100	150	200
	х2	35	50	70	100	35
Выход	у	38	52	61	83	57	84	132

3.2 Выбрать структуру моделей

Критерием выбора той или иной модели является погрешность аппроксимации.

Пример: Для аппроксимации экспериментальных зависимостей

выбираем показательную Т = а₁∙(в₁)^σ и степенную Т = а₂∙(V)^в2 функции.

3.3 Линеаризовать выбранные функции логарифмированием

Пример: После логарифмирования получим lgТ = lga₁ + σlgв₁ и

lgТ = lga₂ + в₂lgV , что эквивалентно линейной зависимости

Y = A + BX

3.4 Получить исходные данные для расчёта параметров моделей метода наименьших квадратов (МНК)

Пример: Таблица 2. Данные для МНК T = f(σ)

№ п/п	σ	lgT	σ2	σ(lgT)
1	σmin
…	…	…	…	…
N	∑σ	∑lgT	∑σ2	∑σ(lgT)

Таблицу 2. повторить для второй частной модели.

: Таблица 3. Данные для МНК T = f(V)

№ п/п	lgV	lgT	(lgV)2	(lgV)(lgT)
1	σmin
…	…	…	…	…
N	∑ lgV	∑lgT	∑(lgV)2	∑(lgV)(lgT)

3.5 Получить систему уравнений

П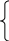 ример:

Для модели T = а₁∙(в₁)^σ имеем (1) Nlga₁ + lgв₁∑σ = ∑(lgT)

lga₁∑σ + lgв₁∑σ² = ∑σ(lgT)

Для модели T = а₂∙(V)^в2 получим аналогично .

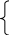(2) Nlga₂ + в₂∑lgV = ∑(lgT)

lga₂∑lgV + в₂∑(lgV)² = ∑(lgT)(lgV)

3.6 Решить систему уравнений и найти величины коэффициентов регрессии

Пример:

Для первой модели получим (3)

lg a₁ = ; lg в₁ = .

Потенцируя найдём параметры модели «а₁» и «в₁». Параметры второй модели найдём аналогично.

lg a₂ = ; (4)

в₂ = .

3.7 Определить среднюю дисперсию всех опытов – дисперсию воспроизводимости

Мерой оценки рассеяния параметра выхода является дисперсия воспроизводимости – средняя дисперсия всех опытов.

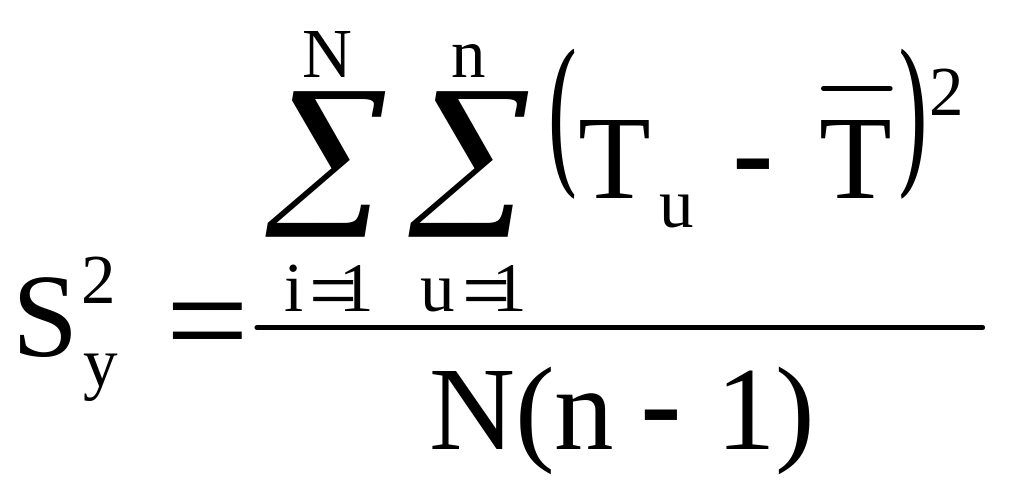, (5)

где u – количество параллельных опытов (1…n=3);

i – количество уровней переменного фактора (точек на кривой отклика) (1…N=4);

– среднее значение выхода из серии параллельных опытов. Вариации параллельных опытов составляют ± (10 – 15)% и рассчитываются самостоятельно.

3.8 Определить дисперсию коэффициентов регрессии

В однофакторных экспериментах дисперсия коэффициентов модели, полученных методом наименьших квадратов, равна

. (6)

3.9 Оценить значимость коэффициентов модели.

Коэффициенты моделей статистически значимы при соблюдении условия

, (7)

где t_p и t_T -расчётный и табличный коэффициенты распределения Стьюдента (Табл. П1 приложения) с достоверностью 95% и степенями свободы f = N(n – 1).

3.10 Объединить частные модели в одну общую многофакторную модель.

Пример:

Дано: частные модели вида: Т = а₁∙(в₁)^σ и Т = а₂∙(V)^в2 .

Приведём любую из моделей к безразмерному виду, разделив её на наименьшее значение выхода.

Пример: Получим m = и, умножив вторую модель на эту величину, будем иметь Y = m∙а₂∙V^в2 = С∙