14-es_1 / Высшая математика (РТФ) / умк_Цывис_Функции_Интеграл. исчисл

Если предел интегральной суммы существует при неограниченном

∫∫∫ f (x, y, z)dxdydz (или ∫∫∫ f (x, y, z)dv ).

Тройной интеграл (1) существует, если:

-функция f(x,y,z) ограниченная;

-функция f(x,y,z) непрерывная;

-ограниченная функция f(x,y,z), все разрывы которой лежат на конеч- ном числе поверхностей с объемом 0.

§3. Свойства интегрируемых функций

итройных интегралов

Сформируем эти свойства (доказательство их аналогично доказа- тельству свойств для двойного интеграла).

1.Существование и величина тройного интеграла не зависит от зна- чений, принимаемых функцией вдоль конечного числа поверхностей с объемом 0.

2.Если V = V1 + V2 , то

∫∫∫ f (M )dV = ∫∫∫ f (M )dV + ∫∫∫ f (M )dV ,

причем из существования интеграла слева следует существование – спра- ва, и обратно.

3.Если C − const , то

∫∫∫C × f (M )dV = C ∫∫∫ f (M )dV .

341

5. Если интегрируема в (V) функция f удовлетворяет неравенству m ≤ f ≤ M , то

m ×V £ ∫∫∫ fdV £ M ×V .

V

§ 4. Вычисление тройного интеграла

Пусть функция f(x,y,z) определена в области

V = {(x, y, z);(x, y) Î D, z1 (x, y) £ z £ z2 (x, y)} ,

где z1 (x, y) и z2 (x, y) – непрерывные функции в квадрируемой области D

(рис. 1).

z

z = z2 (x, y)

V

z = z1 (x, y)

0 y

Теорема. Пусть

1.Существует тройной интеграл

∫∫∫f (x, y, z)dxdydz .

V

342

2. Для любых (x, y) D существует определенный интеграл

Таким образом, вычисление тройного интеграла сводится в этом случае к последовательному вычислению трех определенных (однократ- ных) интегралов

где V – область, ограниченная поверхностями z = 0, z = y, y = x2 , y = 1. Решение. Построим данную область V (рис. 2).

Область V является правильной в направлении оси Oz (вход z = 0 и выход z = y). Ее проекция на плоскость Oxy также правильная в направле- нии оси Oy и оси Ox.

Сведем данный тройной интеграл к повторному

343

y = x2

x

Рис. 2

§ 5. Замена переменных в тройном интеграле

Аналогично случаю двойного интеграла производится замена пере- менных в тройном интеграле

∫∫∫ f (x, y, z)dxdydz ,

1)отображение (1) взаимнооднозначно;

2)функции ϕ(u,v, w), ψ(u,v,w), θ(u,v, w) имеют в области V1 непре-

рывные частные производные первого порядка;

344

3) якобиан преобразования

Тогда справедливо равенство (формула замены переменных в трой- ном интеграле)

Суть замены переменных в тройном интеграле (формула (2) состоит в следующем: интеграл, стоящий в правой части равенства (2) «проще» как по виду функции f(u,v,w), так и по области V1 , чем интеграл и область V

в левой части (2).

Формулы (1) можно рассматривать как формулы перехода к новым, криволинейным координатам (u,v,w) в области V. Поверхности u = const, v = const и w = const представляют собой координатные поверхности (во- обще говоря, криволинейные) в пространстве (x,y,z). Кривые, на которых две криволинейные координаты имеют постоянные значения, и изменяется только одна из координат, представляют собой координатные линии.

Цилиндрические координаты. Пусть M(x,y,z) – произвольная точка в пространстве R3 . M ′ – проекция точки M на плоскость xOy (рис. 1).

z

M(x,y,z)

M (r, ϕ, z)

Рис. 1

345

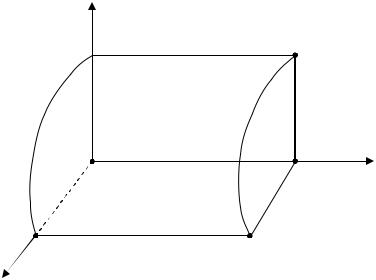
Точка M однозначно задается тройкой чисел (r,j, z), где (r,j) – по- лярные координаты точки M ′ на плоскости xOy; z – аппликата точки M.

Тройка чисел (r,j, z) называется цилиндрическими координатами точки M.

Переход от прямоугольных координат (x,y,z) к цилиндрическим (r,j, z) задается формулами

x = r cos ϕ, y = r sin ϕ, z = z

(3)

(0 £ r < +¥, 0 £ j < 2p, - ¥ < z < +¥)

Якобиан преобразования

Тогда тройной интеграл в цилиндрической системе координат имеет вид

Отметим, что координатные поверхности в рассматриваемом случае будут:

а) r = const – цилиндрические поверхности с образующими, парал- лельными оси z; направляющими для них служат окружности на плоскости xOy с центром в начале координат;

б) j = const – полуплоскости, проходящие через ось z; в) z = const – плоскости, параллельные плоскости xOy.

Таким образом, вычисление тройного интеграла сводится к интегри-

рованию на r, по j и по z аналогично тому, как это делается в декарто- вых координатах.

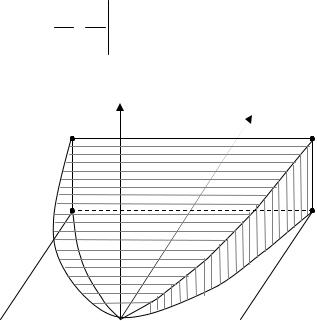
Сферические координаты. Пусть M(x,y,z) – произвольная точка в пространстве R3 . M ′ – проекция точки M на плоскость xOy (рис. 2). Точ-

OM и Oz.

Тройка чисел (r,ϕ,θ) называется сферическими координатами точ-

ки M (или полярными координатами в пространстве).

346

Рис. 2

Переход от прямоугольных координат (x,y,z) к сферическим (r,j,q)

задается формулами

x = r cos j × sin q, y = r sin j × sin q, z = r cos q

(5)

(0 ≤ r < +∞, 0 ≤ ϕ < 2π, 0 ≤ θ ≤ π)

Якобиан преобразования

I = D(x, y, z) = r2 sin q .

D(r,j,q)

Тогда тройной интеграл в сферической системе координат имеет вид

∫∫∫ f (x, y, z)dxdydz = ∫∫∫ f (r cos j × sin q, r sin j × sin q, r cos q)r2 sin qdrdjd q .

V

Отметим, координатные поверхности составляют три семейства:

где V – область, ограниченная поверхностями z = 0 и (z -1)2 = x2 + y2 .

347

Решение. Область V – конус (рис. 3). Уравнение конической поверхности,

ограничивающей область V, запишем в виде z = 1 − x2 + y2 , а саму об-

ласть V: 0 ≤ z ≤ 1 − x2 + y2 , x2 + y2 ≤ 1. Тогда данный тройной интеграл I

можно свести к последовательному вычислению трех определенных инте- гралов в прямоугольных координатах.

y = +1 − x2

–1 D z = 0 1 x

y = −1 − x2

Рис. 3

При вычислении данного интеграла удобнее перейти к цилиндриче- ским координатам x = r cos ϕ, y = r sin ϕ, z = z . Тогда прообраз круга D есть

область V1 , изображенная на рис. 4.

Якобиан перехода к цилиндрическим координатам равен r, подынте-

гральная функция в цилиндрических координатах равна r2 (1 + sin 2ϕ) − z .

348

z

1

z = 1 – r

349

Уравнение сферы в сферических координатах имеет вид r2 = r cos ϕ ,

r

V1

2π ϕ

r = cos θ

π

2

θ

Рис. 6

Пример 3. Поменять порядок интегрирования (различными способами)

1 x xy

в) ∫dx∫dy ∫ f (x, y, z)dz .

0 0 0

Ответы:

350