Решение. Построим область D (рис. 9).
Пусть новые переменные будут u и v. В системе координат uOv по ус- ловию задачи будет прямоугольник (P), который должен быть ограничен прямыми, параллельными координатным осям: u = u1 , u = u2 , v = v1 и v = v2 . Из уравнений линий, задающих границы области D имеем:
xy = 1, xy = 2, x − y = −1, x − y = 1.
y
y = 2 x
|
|
|
|
|
|
|
|
y = |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
–1 |
0 |
|
|
1 |
x |
x |
|
|
|
|
|
|
–1 |
|
|
|
|
|
|
|
|
Рис. 9 |
|
Полагая |
u = xy, |
v = x − y |
|
получим искомое преобразование, а |
прямоугольник (P) |
будет ограничен прямыми |
u = 1, u = 2, v = −1, v = 1 |
(рис. 10). |
|
|
|
|
|
|
|
|
|
|
v
1
–1
Рис. 10
§6. Приложения двойного интеграла
6.1.Вычисление площадей плоских фигур
Площадь S плоской области D, расположенной на плоскости XOY вычисляется в декартовых координатах по формуле
S = ∫∫ f (x, y)dxdy ,
D
а в полярных координатах по формуле
S = ∫∫rdrdϕ .
D
Пример 1. Вычислить площадь плоской фигуры, ограниченной ли-
ниями: y2 = 10x + 25, y2 = −6x + 9 (рис. 1).
Решение. Для построения области D преобразуем уравнения границ, за-
писав их в виде x = |
y2 |
− 2,5 и |
x = − |
y2 |
+ |
3 |
. |
|
|
|
10 |
|
6 |
2 |
|
Каждое из этих уравнений определяет параболу с осью симметрии Ox.
|
|
|
y |
|
B |
|
15 |
|
|
|
3 |
y2 = 10x + 25 |
|
|
|
|
|
|
y2 = 9 − 6x |
–2,5 |
–1 |
0 |
3 |
x |
|
|
|
2 |
 –3
–3
 –
–  15
15
A
Рис. 1
y 2 |
=10x + 25 |
определяем координаты |
Решая систему уравнений |
2 |
= -6x + 9 |
y |
|
точек A(-1;-
 15) и B(-1;
15) и B(-1; 
 15) .
15) .
Отметим, что внешние пределы интегрирования удобнее взять по y, так как в противном случае область интегрирования нужно разбивать на две части и соответственно вычислять два интеграла. Учитывая симмет- рию области D относительно оси Ox , получим
|
|
|
|
− |
y 2 |
+ |
3 |
|
|
|
|
|
|
15 |
6 |
2 |
|
16 |
|
|
|
S = ∫∫dxdy = 2 ∫dy |
|
|
∫dx = |
15 . |
|
|
|
D |
0 |
|
y 2 |
3 |
|
|
|
|
|
|
|
|
|
− 2,5 |
|
|
|
|
10 |
|
|
|
|
|
|
|
|
|
|
|
|
Пример 2. Вычислить площадь плоской фигуры, заданной неравен- |
ствами: x2 + y2 ³ 4 y, x2 + y2 £ 8 y, |
|
y ³ -x . |
Решение. Данная фигура имеет границы, заданные уравнениями окружно- стей и лучом, выходящим из начала координат, но для вычисления площа- ди целесообразно перейти к полярным координатам (рис. 2)
y
r = 8sin ϕ
D
y = – x
4
r = 4sin ϕ 2
Рис. 2
Тогда
|
3 |
π |
8 sin ϕ |
|
4 |
|
|
S = ∫∫rdrdj = |
∫ dj |
∫ rdr . |
D |
0 |
4 sin ϕ |
6.2.Вычисление объемов тел
Объем тела, ограниченного сверху поверхностью z = f (x, y) , снизу
областью D плоскости XOY, а сбоку цилиндрической поверхностью, обра- зующие которой параллельны оси Oz (рис. 3, 4), находится по формуле
V = ∫∫ f (x, y)dxdy .
|
|
|
D |
|
|
z |
|
z |
z = f(x,y) |
|
|
z = f(x,y) |
|
V |
|
|
|
|
|
|
V |
|
z = g(x,y) |
|
0 |
y |
|
|
0 |
y |
|
|
|
|
|
D |
|
D |
|
|
|
|
|
x |
|
x |
|
|
|
|
|
|
Рис. 3 |
|
|
Рис. 4 |
|
Пример 3. С помощью двойного интеграла вычислить объем тела, |
|
ограниченного поверхностями: 2x + 3y + z – 6 = 0, |
x + 3y = 3, x = 0, z = 0. |
|
Решение. Уравнение |
|
|
|
2x +3y + z – 6 = 0
определяет плоскость, которая на координатных осях OX, OY, OZ отсекает соответственно от- резки 3, 2 и 6. Уравнение
x + 3y = 3
на плоскости XOY определяет прямую, а в пространстве – плоскость, параллельную оси Z. Данное тело ограничено сверху плоскостью 2x + 3y + z – 6 = 0, а снизу – плоскостью z = 0 (рис. 5).
Проекция данного тела на плоскость XOY имеет следующий вид
(рис. 6).
y
2
2x + 2y – 6 = 0
Рис. 6
Тогда объем искомого тела
|
|
2 − |
2 |
x |
|
|
|
|
|
3 |
|
|
|
|
|
|
3 |
|
|
|
|
3 |
|
V = ∫∫(6 − 2x − 3y)dxdy = ∫dx |
|
∫(6 |
− 2x − 3y)dy = |
. |
|
|
D |
0 |
|
3− x |
|
|
2 |
|
|
|
3 |
|
|
|
|
|
|
Пример 4. Вычислить объем тела, ограниченного снизу плоскостью |
XOY, сверху – плоскостью 2 – x – |
y – 2 z = 0, с боков – |
цилиндрической по- |
верхностью y = x2 и плоскостью y = x. |
|
|
|
|
|
|
|
|
|
Решение. Построим данное тело (рис. 7) |
|
|
|
|
|
|
|
|
|
z
1
1
2 x
Рис. 7

Проекция данного тела на плоскость XOY имеет вид (рис. 8)
y
y = x2
y = x
1
Рис. 8
|
Подынтегральная функция |
f (x, y) = |
1 |
(2 − x − y) . |
|
|
|
|
|
|
2 |
|
|
|
|
Тогда объем искомого тела |
|
|
|
|
|
|
1 |
x |
1 |
|
|
|
11 |
|
|
V = ∫dx ∫ |
(2 − x − y)dy = |
. |
|
|
|
|
0 |
x 2 |
2 |
|
|
120 |
|
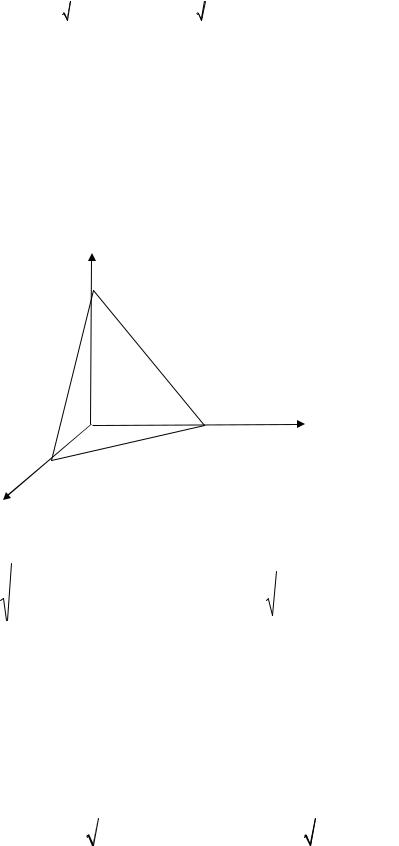
Пример 5. Оси двух круговых цилиндров с одинаковыми попереч- ными сечениями пересекаются под прямым углом. Вычислить объем об- щей части этих цилиндров.
Решение. Выберем прямоугольную систему координат в пространстве та- ким образом, чтобы оси цилиндров совпадали с осями OY и OZ, а радиус поперечного сечения каждого из цилиндров равен r. Тогда уравнения ци- линдрических поверхностей будет иметь вид:
-x2 + z 2 = r 2 – цилиндрическая поверхность с осью симметрии Oy;
-x2 + y 2 = r 2 – цилиндрическая поверхность с осью симметрии Oz.
Построим данное тело (рис. 9).
На рис. 9 отмечена одна восьмая часть тела, полученного пересече- нием двух цилиндров. Подынтегральная функция – это уравнение, разре- шенное относительно y (уравнение поверхности цилиндра с осью симмет- рии Oy), т.е.
f (x, y) = 
 r 2 − x2
r 2 − x2
z
y
x
Рис. 9
Проектируя ее часть, отрезанную второй поверхностью и содержа- щуюся в первом октанте, получим область интегрирования – это часть кру-
га x2 + y 2 ≤ r 2 , расположенная в первой четверти плоскости XOY. Поэто-
му, имеем
|
|
|
|
|
|
|
|
|
|
|
|
|
x3 |
|
x = r |
|
|
|
|
|
1 |
r |
r 2 − x 2 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
2 |
|
|
2 |
|
|
3 |
|
|
V = ∫dx ∫ |
r |
− x |
dy = |
|
x − |
|
|
|
|
= |
|
r |
. |
8 |
|
|
r |
|
3 |
|
|
|
3 |
|
0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
x = 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Следовательно V = 16 r 3 . 3
Пример 6. Вычислить объем тела, ограниченного поверхностями
x2 + y 2 = 4x, z = x, z = 2x .
|
|
|
|
z |
Решение. |
|
|
|
|
|
|
Поверхность |
|
|
|
|
|
x2 + y 2 = 4x есть круговой цилиндр |
|
|
|
|
|
|
|
|
|
|
(x − 2)2 + y 2 = 22 , а z = x и z = 2x – |
|
|
|
|
|
плоскости, проходящие через ось OY |
|
|
|
|
|
под разными углами наклона к плос- |
x |
4 |
2 |
|
0 |
кости XOY. Данные плоскости пересе- |
|
кают цилиндр, |
вырезая клинообраз- |
|
|
|
|
|
|
|
|
|
|
ный слой (рис. 10), объем которого |
|
|
|
y |
|
требуется найти. |
|
|
|
|
Искомый объем найдем как разность |
|
|
|
|
|
|
|
Рис. 10 |
|
|
объемов двух |
цилиндрических тел, |
|
срезанных сверху плоскостями z = 2x (f(x,y) = 2x) |
и z = x (f(x,y) = x). Тогда |
|
|
|
|
|
|
|
|
|
|
|
1 |
4 |
4 x − x2 |
4 |
4 x − x2 |
|
|
|
V = ∫dx |
∫ |
2xdy − ∫dx |
∫ |
xdy = 4π . |
|
2 |
|
0 |
0 |
0 |
0 |
|
|
|
|
|
|
|
Значит V = 8π .
6.3.Вычисление площадей поверхностей
Пример 7. Вычислить площадь той части плоскости 6x + 3y + 2z = 12 , которая заключена в первом октанте.
Решение. Построим поверхность, площадь которой требуется найти (рис. 11).
z
6
|
|
|
|
0 |
|
|
|
4 |
|
|
y |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 11 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dz 2 |
dz 2 |
2 4 − 2 x |
|
|
|
|
|
|
|
|
|
9 |
|
|
Тогда S = ∫∫ 1 + |
|
|
+ |
|
|
dxdy = ∫dx |
∫ |
1 + 9 + |
|
dy = 14 . |
|
|
4 |
P |
dx |
dy |
0 |
0 |
|
|
|
|
Таким образом, |
S = 14 . |
|
|
|
|
|
|
|
|
|
|
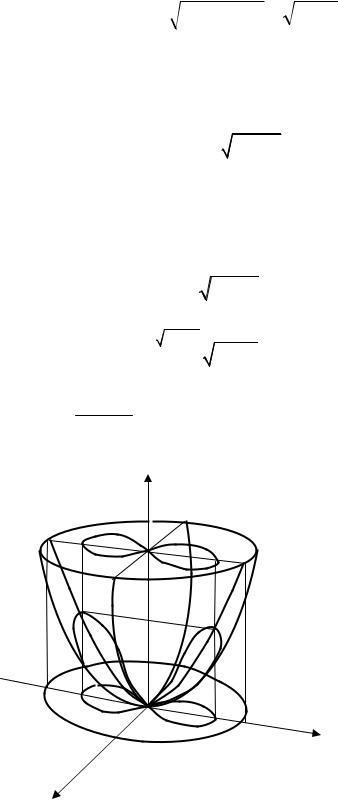
Пример 8. Вычислить площадь части поверхности параболоиды |
2x = x2 + y 2 , вырезанной цилиндром |
(x2 + y 2 )2 = x2 − y 2 . |
|
|
|
Решение. Построим поверхность, площадь которой требуется вычислить
(рис. 12).
Границей проекции вырезанной части на плоскость XOY будет лем- ниската. Цилиндр вырезает из параболоида две равные поверхности. Так
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z = |
|
2 |
+ y |
2 |
|
′ |
2 |
′ |
2 |
|
|
|
2 |
|
2 |
|
|
как |
|
(x |
|
|
) , то S = ∫∫ |
1 + (Z x) |
|
+ (Z y) |
|
dxdy = ∫∫ |
1 + x |
|
+ y |
|
dxdy . |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
P |
|
|
|
|
|
P |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Переходя к полярным координатам, имеем
x = r cos ϕ; y = r sin ϕ; 
 1 + x2 + y2 =
1 + x2 + y2 = 
 1 + r2
1 + r2
уравнение лемнискаты
(r2 + cos2 ϕ + r2 sin2 ϕ)2 = r2 cos2 ϕ − r2 sin2 ϕ
или |
|
r4 = r2 cos 2ϕ, |
r = ± cos2ϕ . |
В силу того, что параболоид и цилиндр симметричны относительно плоскостей XOY и YOZ, то достаточно вычислить интеграл по одной чет- верти лемнискаты, расположенной в первой четверти плоскости XOY. То- гда будем иметь
|
0 ≤ ϕ ≤ π , 0 ≤ r ≤ |
|
|
|
. |
|
|
|
cos 2ϕ |
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
π |
|
|
|
|
|
|
|
|
|
|
1 |
4 |
cos 2ϕ |
|
|
|
|
|
20 − 3π |
|
|
А искомая площадь |
S = ∫ dϕ |
∫ |
|
1 + r 2 |
rdr = |
. |
|
|
|
|
4 |
0 |
0 |
|
36 |
|
|
|
|
|
|
|
|
|
|
|
Таким образом, S = 20 − 3π . 9
z
y
x
Рис. 12
|
МОДУЛЬ 5. ТРОЙНОЙ ИНТЕГРАЛ |
|
§1. Задача о вычислении массы тела |
|
Пусть дано некоторое тело V, плотность в каждой точке M(x, y, z) |
равна |
ρ(x, y, z) . Определить массу m данного тела. Для решения данной |
задачи поступим следующим образом: |
− |
разбиваем область V на n частей Vi , объемы которых Vi ; |
- |
в каждой из Vi (i = |
|
) выбираем по точке Mi (i = |
|
) ; |
1, n |
1, n |
-считаем, что в пределах каждой из частей DVi плотность прибли-
женно постоянна и равна плотности ρ(Mi ) в выбранной точке;
- тогда масса mi этой части DVi (i =1, n) будет приближенно равна
mi = DVi ×r(Mi ) ;
V определим по формуле
|
n |
|
n |
lim |
∑mi |
= lim |
∑r(Mi ) × DVi |
n →∞ |
→0) i =1 |
n →∞ |
i =1 |
(max V |
|
i |
|
|
|
и, следовательно, задача решена.
Этот физический пример приводит к общему определению тройного интеграла, который является обобщением определенного интеграла на случай функции трех переменных.
§2. Определение тройного интеграла
иусловия его существования
Пусть в некоторой пространственной области (V) задана функция f(x,y,z). Разобьем эту область на конечное число частей (Vi ) (i =1, n) ,
имеющих соответственно объемы DVi (i =1, n) . В пределах i-того элемента
(Vi ) выбираем точку Mi (xi , yi , zi ) , значение функции в этой точке f (Mi )
умножим на DVi , получим интегральную сумму
n
Ii = ∑ f (xi , yi , zi ) Vi .
i =1




 –3
–3 –
–  15
15

 15)
15) 
 15) .
15) .






 1 +
1 + 
 1 +
1 + 