Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Пензенский Государственный Университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

умк_Цывис_Функции_Интеграл. исчисл

..pdf

Скачиваний:

Добавлен:

18.05.2015

Размер:

4.7 Mб

Скачать

☆

<<< < Предыдущая 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 2728 / 3628 29 30 31 32 33 34 35 36 > Следующая >>>

4. Длина дуги пространственной кривой.

По отношению к пространственной кривой

x = ϕ(t), y = ψ(t), z = λ(t)

без кратных точек – определение длины дуги дается в таком же виде, как и для плоской кривой. В этом случае получается формула длины дуги, ана- логичная, как и для плоской кривой с учетом третьей координаты, т.е.

l = ∫ (xt¢)2 + ( yt¢)2 + (zt¢)2 dt .

Пример 22. Вычислить длину винтовой линии x = a cos t, y = a sin t, z = ct от точки А(t = 0) до точки М (t – любая).

Решение. В данном случае имеем

(xt¢)2 + ( yt¢)2 + (zt¢)2 = a2 + c2 ,

тогда

l = ∫ a2 + c2 dt = a2 + c2 t .

Этот результат действительно такой, потому что при разворачивании цилиндрической поверхности винтовая линия на ней превратится в на- клонную прямую.

Пример 23. Вычислить длину кривой Вивиани

x = R sin2 t, y = R sin t cost, z = R cost

Решение. В данном случае имеем

(x¢)2	+ ( y¢)2	+ (z¢)2	= R × 1 + sin2 t .
t	t	t

Тогда длина кривой выразится эллиптическим интегралом 2-го рода

π π π

2		2			2		1			1

l = 4R ∫	1 + sin2 tdt = 4R ∫		1 + cos2 t = 4	2	R ∫	1 -		sin2 tdt = 4	2RE		.

0	0		0			2				2

5. Длина дуги, заданной в полярных координатах.

Получим формулу для длины дуги кривой в случае, когда уравнение кривой задано в полярных координатах

ρ = f (θ) .

271

Для получения формулы длины дуги, заданной в полярных коорди- натах, используем формулу для длины дуги в параметрической форме. Так как соотношение между декартовыми и полярными координатами точки имеют следующий вид

x = ρcos θ,

y = ρsin θ ,

а ρ и θ связаны уравнением кривой

ρ = f (θ) , то, как x, так и y можно

выразить через одну переменную (параметр) θ:

x = ρcos θ = f (θ)cos θ;

y = ρsin θ = f (θ)sin θ .

Таким образом, получаем, что искомая кривая задана в параметриче-

ской форме, тогда

′

= ρ cos θ − ρsin θ,

= ρ sin θ + ρcos θ

′ 2

′

+ ρ

(x )

+ ( y )

= (ρ )

а следовательно

θ2

l =

′

+ ρ

d θ ,

∫ (ρ )

где ρ = f (θ), ρ

′

θ1

(θ) .

При этом соответствующая формула для дифференциала дуги в по- лярных координатах

(de)2 = (dp)2 + ρ2 (d θ)2 .

Пример 24. Вычислить длину кар- диоиды ρ = a(1 − cos θ)

Решение. Кардиоида симметрична относи- тельно Ox и в начале координат имеет точку возврата, а касательная совпадает с осью Ox.

Мы получим половину длины кар- диоиды, при изменении полярного угла от 0 до π. Тогда

l	π				π
	π				π
	= a∫ (1 − cos θ)2 + sin2 θd θ = a∫						d θ =
						2 − 2cos θ
2						2 − 2cos θ
2	0				0
	0				0
		π		π	θ d θ = 4a.
		π		π
	= a∫		4sin2 θ d θ = 2a∫sin
	0		2	0	2
	0			0

Следовательно, длина всей кардиоиды равна 8a.

272

Пример 25. Найти длину замкнутой кривой r = a sin3 ϕ . 3

Решение. Так как r ³ 0 , то sin ϕ ³ 0 , откуда 0 £ j £ 3p. При изменении j

от 0 до	3	p радиус-вектор r	возрастает от 0 до	a, а конец радиус-
от 0 до		p радиус-вектор r	возрастает от 0 до	a, а конец радиус-
2
вектора описывает дугу ОАМВ.
		A
		M	C	x
0

				B
А при изменении		j от			3	p до			3π величина				ρ		убывает от a до 0,
А при изменении		j от			2	p до			3π величина				ρ		убывает от a до 0,
					2
при этом описывая дугу			ВСАО, симметричную дуге ОАМВ относительно
прямой j = π или j = - π .
2			2
Тогда имеем
				r¢	= a sin2 j cos j;
				ϕ					3	3
									3	3
														= a sin2 j;
				a2 sin6 j + a2 sin4 j cos2 j
	r2 + (r¢ )2	=		a2 sin6 j + a2 sin4 j cos2 j
	ϕ						3			3			3		3
							3			3			3		3
	3π		2	j			a	3π			2j				3ap
	l = a ∫ sin			dj =				∫	(1 - cos			)dj =				.
	l = a ∫ sin			dj =			2	∫	(1 - cos			)dj =			2	.
0				3			2	0		3					2
0								0

Пример 26. Вычислить длину первого витка архимедовой спирали

r = a × j.

Решение. Первый виток архимедовой спирали образуется при изме- нении полярного угла j от 0 до 2π. Следовательно, имеем

2π		2π			1
2π		2π

l = ∫	a2j2 + a2 dj = a ∫		j2 + 1dj = a p	4p2 + 1 +		ln(2p +	4p2 + 1 .
l = ∫	a2j2 + a2 dj = a ∫		j2 + 1dj = a p	4p2 + 1 +	2	ln(2p +	4p2 + 1 .
0	0				2
0	0

273

8.5.Объем тела

1.Понятие объема тела. Понятие объема вводится аналогично по- нятию площади. При конструктивном определении объема рассматрива- ются кубильяжи, т.е. разбиение пространства на одинаковые кубы.

Рассмотрим кубильяж, у которого длина ребер кубов равна

10n

Пусть пространственная фигура (тело) F содержит фигуру, составленную

из an

кубов этого кубильяжа, и содержится в фигуре,

составленной из

таких кубов. Тогда

– значение объема фигуры

F с недостатком, а

103n

– с избытком.

Если фигура F такова, что пределы

V (F ) = lim

= lim

V (F )

n →∞ 103n

n→∞ 103n

совпадают, то фигура F называется кубируемой, а число V (F ) =

на-

V (F )

зывается объемом фигуры

F и обозначается через V(F). Объем V есть

функция, заданная на множестве всех кубируемых фигур и принимающая неотрицательные значения.

Как и площадь, объем может быть определен аксиоматически, при- чем аксиомы, на которых основывается понятие объема, совершенно ана-

логичны аксиомам площади:
1)	функция	V неотрицательна, т.е.	V (F ) ³ 0 для любой кубируемой
фигуры (тела);
2)	функция	V аддитивна, т.е. если	F1 и F2 – кубируемые фигуры,
не имеющие общих внутренних точек, то
		V (F1 F2 ) = V (F1 ) + V (F2 );
3)	функция	V инвариантна относительно перемещений, т.е. если F1
подобна	F2 , то V (F 1) = V (F2 ) ;
4)	единичный куб (т.е. куб, ребро которого имеет длину 1) имеет

объем 1.

Как и для случая площадей, имеет место теорема существования и единственности.

274

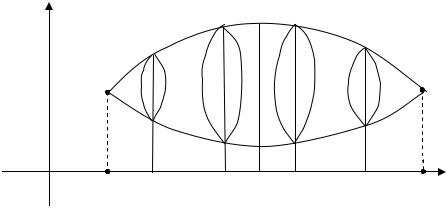
2. Метод вычисления объемов методом сечений.

Пусть дано некоторое тело Т, объем которого требуется вычислить. Проведем сечения этого тела плоскостями, перпендикулярными оси Ox (поперечные сечения). Считаем, что в сечении получаются фигуры, пло- щадь которых мы сможем вычислить. Отметим, что построенные сечения будут иметь площадь S(x) – функция от x, x [ab] . Тогда объем тела, за-

ключенного между двумя сечениями x = a и x = b, определим следую- щим образом.

x0	ci			xn x
a	xi−1	xi		b
Считаем, что данное тело имеет такую форму, что каждое сечение –
квадрируемая фигура, площадь которой		S(x),	причем	S(a) = S(b) = 0, а
функция S(x) непрерывна на	[a,b] . Отрезок		[a,b]	разбиваем на части
точками деления:
a = x0 < x1 < x2 < ... < xn −1 < xn = b ;

внутри каждого отрезка [ xi −1, xi ] выберем произвольную точку ci и про-

ведем через нее сечение x = ci , перпендикулярное к оси Ox; тогда тело Т разобьется на слои. Каждый i-тый слой заменим цилиндром, имеющим ос- нованием сечение, проходящее через точку ci , а высоту – расстояние ме-

жду двумя сечениями, т.е. величина [ xi −1, xi ] = xi . Тогда Vi = S (ci ) × Dxi , а

V = lim ∑Vi

n →∞ i =1

= lim ∑S (ci )

n →∞ i =1

xi = ∫S (x)dx .

Следовательно, рассматриваемый объем равен

V = ∫S (x)dx ,

где S(x) – площадь поперечного сечения тела, проведенного через x пер- пендикулярно оси Ox.

275

Пример 27. Вычислить объем трехосного эллипсоида, т.е. тела, по- верхность которого выражается уравнением

x2	+	y2	+	z2	=1.
a2		b2		c2

Решение. Сечение, перпендикулярное к оси Ox есть эллипс

y2	+	z2	=1 -	x2	,
b2		c2		a2

полуоси которого соответственно равны

b 1 -

и c 1 -

Площадь эллипса

S = pa × b , где a и b –

но, площадь рассматриваемого сечения

S (x) = p × bc 1

а объем эллипсоида

V =

∫

pbc 1

= pbc x

−a

его полуоси. Следователь-

= 4 pabc .

−a

Отметим, что если a = b = c = r , то мы получим шар, и V = 4 pr3 . 3

Пример 28. Вычислить объем пирамиды высотой Н и площадью основания S0 .

Решение. Рассмотрим четырехугольную пирамиду. Вершину пирамиды S примем за начало координат, а ось Ox направим по высоте Н пирамиды к основанию.

S 0

S(x)

S(0)

276

Проведем сечение пирамиды плоскостью, параллельной основанию

и отстоящей от вершины S на расстоянии

0 ≤ x ≤ H . Площадь этого

сечения является функцией от x, т.е. пусть она равна S(x).

В силу свойств сечений пирамиды, параллельных основанию имеем

S (x)

H 2

Откуда получим

S (x) =

x2 .

Тогда объем пирамиды равен

H 2

V = ∫ S (x)dx = ∫

x2dx =

S0 H .

H 2

0 3

Пример 29. Вычислить объем тела, ограниченного однополостным

гиперболоидом

и плоскостями z = 0, z = h (h > 0).

Решение. В данном примере рассмотрим сечения, перпендикулярные оси Oz, т.е. искомый объем

V (z) = ∫S (z)dz ,

где S(z) – площадь сечения, перпендикулярная оси z. Определим функцию S(z)

=1 +

Тогда полуоси эллипса

a =

a2 1 +

;

b = b2

а его площадь находим по формуле

S (z) = pa b = pab 1

1 1

Тогда искомый объем

V = pab

∫

1 +

dz = pabh 1 +

277

Пример 30. Оси двух одинаковых цилиндров с радиусами основа- ния, равными r, пересекаются под прямым углом. Вычислить объем тела, составляющего общую часть этих двух цилиндров.

Решение. Пусть оси цилиндров совпадают с Oy и Oz.

Тогда ОАВСD –	1	часть искомого объема. Проведем сечение этого

8

тела плоскостью, перпендикулярной оси Ox, на расстоянии x от начала координат. Сечение – это квадрат EFKL, сторона которого вычисляется по

формуле EF =

r2 - x2 , а площадь

S (x) = r2 − x2 ,

следовательно,

иско-

мый объем

V = 8∫(r2 - x2 )dx =

r3 .

Замечание. Рассмотрим эту за-

дачу для случая, в котором цилиндры

имеют различные радиусы r и R > r.

Отличие по сравнению с рассматри-

ваемым выше примером лишь в том,

что вместо квадрата, в сечении рас-

сматриваемого тела плоскостью по-

0 F A

лучится прямоугольник со сторона-

ми r2 - x2 и R2 - x2 .

Тогда

искомый

объем

V = 8∫ (R2 - x2 )(r2 - x2 )dx .

Сделав подстановку

x = r sin j,

k =

, получим

V = 8Rr2 ∫ cos2 j ×

1 - k 2 sin2 jdj.

Данный интеграл эллиптический интеграл, для вычисления которого используем соответствующие таблицы.

Пример 31. Определить объем геометрического тела, отсекаемого от прямого кругового цилиндра плоскостью, проходящей через диаметр ос- нования цилиндра (рис. 1)

278

								L
		P			L	S1
		P			L			h	y
								h	y
x		N		h		x
x	α	N		h		S
A1		y				S
A1		y				A1		K
	M					A1		K
	M
		x			y	α	M		Q
		α	a	K		α	M		Q
		α	a	K			y
		O					y
		O

A	A
Рис. 1	Рис. 2

Считаем,

что

основание цилиндра

есть

круг

радиуса

а,

т.е.

x2 + y2 ≤ a2 , и что секущая плоскость проходит через диаметр

и со-

ставляет угол a с плоскостью основания.

Определим площадь сечения, перпендикулярного к оси x и пересе-

кающего ее в точке

М. Это сечение – прямоугольный треугольник,

пло-

щадь которого

S (x) = S MNP =

y2 × tga =

(a2 - x2 ) × tga .

Тогда искомый объем

V =

tga ∫ (a2 - x2 )dx =

a3tga =

a2 h .

−a

Отметим, что тот же объем можно найти, построив сечение, перпен-

дикулярное оси

Oy (рис. 2). Секущая плоскость, проходящая через точку

М с ординатой

пересекает данное тело по прямоугольнику

S1SQQ1 ,

площадь которого

S ( y) = 2xytga = 2tga × y ×

a2 - y2 .

Тогда искомый объем

V = 2tga∫ y a2 - y2 dy =

tga × (a2 - y2 )

a3tga =

a2h .

279

3. Принцип Кавальери для объемов.

				Если в пространстве заданы два те-
				Если в пространстве заданы два те-
		A		ла V1 и V2 , и любая плоскость, парал-
N	R		E M	лельная данной, в сечении с этими тела-
N	R		E M	ми образует две фигуры, площади кото-
	C			ми образует две фигуры, площади кото-
	C			рых равны друг другу: S1 = S2	(при этом
				рых равны друг другу: S1 = S2	(при этом
	O			сечения каждого тела, вообще говоря,
				являются переменными). Тогда два тела
				имеют равные объемы V1 = V2 .
		B		имеют равные объемы V1 = V2 .	R и опи-
		B		Возьмем круг радиуса
				Возьмем круг радиуса
	Рис. 3			шем около него квадрат. Проведем диа-
	Рис. 3			гонали квадрата (рис. 3) и, вращая рису-
				гонали квадрата (рис. 3) и, вращая рису-
				нок вокруг вертикальной оси АВ, полу-
чим шар радиуса			R, описанный около шара цилиндр и вписанный в ци-

линдр «двойной» круговой конус с вершиной в центре шара О. На рис. 4 показаны эти три тела.

–

Рис. 4

Возьмем точку С на оси вращения АВ на некотором расстоянии x от центра шара и проведем через С горизонтальную плоскость (MN). Эта плоскость в сечении с цилиндром образует круг радиуса CM = R , в сече-

нии с конусом – круг радиуса CD = OC = x (т.к. угол при вершине кону-

са прямой) и в сечении с шаром –

круг радиуса

. По теореме Пифаго-

ра имеем

2 =

2 +

или

2 =

2 +

2 .

Умножая обе части последнего соотношения на число π, получим p × CM 2 = p CE 2 + p CD 2 , т.е.

280

<<< < Предыдущая 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 2728 / 3628 29 30 31 32 33 34 35 36 > Следующая >>>

Соседние файлы в папке Высшая математика (РТФ)

#
18.05.20154.76 Mб48умк_Вакульчик_Элементы векторной алгебры.pdf
#
18.05.20155.38 Mб53умк_Вакульчик_Элементы линейной алгебры.pdf
#
18.05.20151.33 Mб54умк_Мальцев_Осн дискретной матем.pdf
#
18.05.20153.75 Mб62умк_Пальчик_Теория вероятностей.pdf
#
18.05.20155.68 Mб42умк_Цывис_Диф.уравнения_Ряды.pdf
#
18.05.20154.7 Mб52умк_Цывис_Функции_Интеграл. исчисл..pdf
#
18.05.20153.54 Mб100умк_Яско_ Диф.уравнения_Ряды.pdf