
- •Содержание дисциплины
- •Тема 1. Краткие сведения из теории чисел
- •2. Наибольший общий делитель (нод). Алгоритм Евклида.
- •4.Взаимно простые числа. Наименьшее общее кратное (нок).
- •5. Простые и составные числа. Основная теорема арифметики.
- •7. Целые систематические числа.
- •8. Конечные и бесконечные десятичные дроби.
- •10. Решение уравненияв целых числах для целых чисел.
- •11. Признаки делимости.
- •Тема 2. Краткие сведения из алгебры многочленов
- •4. Деление с остатком в . Схема Горнера.
- •5. Наибольший общий делитель. Взаимная простота и неприводимость.
- •6. Многочлены над полем комплексных чисел .
- •7. Многочлены над полем действительных чисел.
- •8. Многочлены над полем рациональных чисел .
- •9. Нахождение рациональных корней многочленов с рациональными коэффициентами.
- •10. Освобождение от алгебраической иррациональности в знаменателе.
- •11. Симметрические многочлены и их применение.
- •Вариант 1
- •Вариант 2
- •Вариант 3
- •Вариант 4
- •Вариант 5
- •Вариант 6
- •Вариант 7
- •Вариант 8
- •Вариант 9
- •Вариант 10
- •Вариант 11
- •Вариант 12
- •Вариант 13
- •Вариант 14
- •Вариант 15
4. Деление с остатком в . Схема Горнера.
Определение. Разделить с остатком
многочлен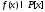 на ненулевой многочлен
на ненулевой многочлен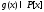 - значит найти многочлены
- значит найти многочлены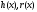
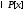 такие, что
такие, что
1)
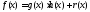 и 2)
и 2)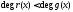 .
.
При этом многочлен
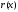 называетсяостатком, а
называетсяостатком, а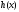 -неполным частным.
-неполным частным.
Теорема 8.2.(О делении многочленов
с остатком в ).
Для любых многочленов
).
Для любых многочленов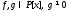 существуют, причём единственные
многочлены
существуют, причём единственные
многочлены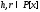 такие, что 1)
такие, что 1)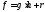 и 2)
и 2) .
.
Таким образом, деление с остатком любого многочлена на ненулевой многочлен с коэффициентами из одного и того же поля всегда возможно, причём единственным образом.
Деление с остатком многочленов производится, как и для натуральных чисел, уголком, начиная с верхнего правого угла.
Схема Горнера– это алгоритм деления
с остатком многочлена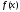 на
на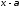 .
.
Если
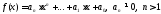 ,
то по теореме Безу существует единственный
многочлен
,
то по теореме Безу существует единственный
многочлен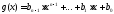 такой, что
такой, что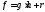 .
Тогда
.
Тогда
получаем следующую систему соотношений:

Замечаем следующую зависимость:
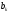 получается как сумма
получается как сумма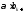 и
и .
Заготовкой для вычислений является
таблица:
.
Заготовкой для вычислений является
таблица:
|
|
|
|
|
…. |
|
|
|
|
|
|
|
|
|
|
Для того, чтобы заполнить первую слева
незаполненную клеточку во второй строке,
нужно
 умножить на элемент, стоящий в предыдущей
клеточке второй строки, и результат
сложить с элементом, стоящим над
вычисляемой клеточкой в первой строке.
умножить на элемент, стоящий в предыдущей
клеточке второй строки, и результат
сложить с элементом, стоящим над
вычисляемой клеточкой в первой строке.
Все дальнейшие вычисления производим в таблице:
|
|
|
|
|
…. |
|
|
|
|
|
|
|
…. |
|
|
Пример 17. Разделить с остатком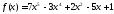 на
на .
.
В данном случае
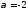 .
Заполняем заготовку:
.
Заполняем заготовку:
|
|
7 |
-3 |
0 |
2 |
-5 |
1 |
|
-2 |
7 |
|
|
|
|
|
Далее производим вычисления:
|
|
7 |
-3 |
0 |
2 |
-5 |
1 |
|
-2 |
7 |
-17 |
34 |
-66 |
127 |
-253 |
Значит,
 .
.
В частности,
 .
.
Схема Горнера применяется во многих случаях. В частности, при определении кратности корня многочлена.
Определение. Пусть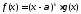 ,
где
,
где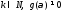 .
Тогда
.
Тогда называетсякорнем кратности
называетсякорнем кратности
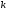 многочлена
многочлена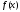 .
Если
.
Если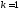 ,
то
,
то называетсяпростымкорнем.
называетсяпростымкорнем.
Пример 18.Найти кратность корня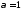 многочлена
многочлена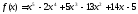 .
.
По теореме Безу кратность корня
 равна количеству делений
равна количеству делений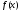 на
на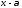 с нулевым остатком. Все вычисления
выполняем в одной таблице:
с нулевым остатком. Все вычисления
выполняем в одной таблице:
|
|
1 |
-2 |
5 |
-13 |
14 |
-5 |
|
1 |
1 |
-1 |
4 |
-9 |
5 |
0 |
|
1 |
1 |
0 |
4 |
-5 |
0 |
|
|
1 |
1 |
1 |
5 |
0 |
|
|
|
1 |
1 |
2 |
7 |
|
|
|
Значит,
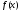 ⋮
⋮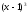 ,
но не делится на
,
но не делится на .
Поэтому кратность корня
.
Поэтому кратность корня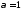 многочлена
многочлена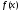 равна 3.
равна 3.
Заметим, что при вычислении значений в третьей и т.д. строках таблицы, требуемые по схеме Горнера числа брали из стоящей выше строки.
5. Наибольший общий делитель. Взаимная простота и неприводимость.
Определение.Многочлен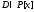 называетсяобщим делителем(ОД)
многочленов
называетсяобщим делителем(ОД)
многочленов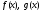 ,
если каждый из этих многочленов делится
наD.
,
если каждый из этих многочленов делится
наD.
Многочлен dназывается
наибольшим общим делителем многочленов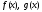 ,
если 1)d- ОД этих
многочленов; 2)dделится
на любой ОД многочленов
,
если 1)d- ОД этих
многочленов; 2)dделится
на любой ОД многочленов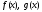 .
.
Обозначение.Нормированным НОД
многочленов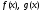 называется такой НОД, старший коэффициент
которого равен 1. Обозначим его через
(
называется такой НОД, старший коэффициент
которого равен 1. Обозначим его через
(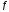 ,
,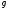 ).
).
Теорема 9.2(Об определяющих свойствах НОД).
1)Если НОД двух многочленов существует, то он определён с точностью до ассоциированности.
2)Если
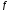 ⋮
⋮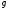 и
и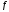 нормирован, то(
нормирован, то(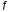 ,
,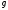 )=
)=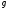 .
.
3)Если
 ,
где
,
где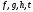 - многочлены из
- многочлены из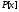 и
и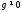 ,
то
,
то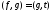 .
.
4)Если хотя бы один из многочленов
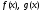 не равен0, то их НОД существует.
не равен0, то их НОД существует.
Алгоритм Евклидаили метод
последовательного деления с остатком
применим и в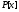 .Но
в случае многочленов модуль (норма в
.Но
в случае многочленов модуль (норма в )
заменяется на степень (норма в
)
заменяется на степень (норма в ).
Пусть
).
Пусть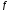 и
и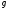 – ненулевые многочлены. Делим
– ненулевые многочлены. Делим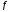 на
на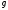 с остаткомr1.
Еслиr1≠0,
то делим
с остаткомr1.
Еслиr1≠0,
то делим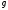 с остаткомr2наr1. Еслиr2≠0,
то делимr1наr2с
остаткомr3и т.д. до тех пор, пока очередной остатокrn+1не станет равным нулю:
с остаткомr2наr1. Еслиr2≠0,
то делимr1наr2с
остаткомr3и т.д. до тех пор, пока очередной остатокrn+1не станет равным нулю:
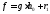 ,
где
,
где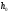 ,r1– многочлены
из
,r1– многочлены
из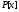 и
и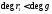 ,
,
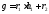 ,
где
,
где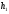 ,
r2 - –
многочлены из
,
r2 - –
многочлены из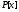 и
и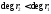 ,
,
………………
rn-2=rn-1∙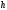 n-1+rn,
где
n-1+rn,
где
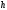 n-1,
rn
-– многочлены из
n-1,
rn
-– многочлены из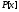 и
и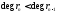 ,
,
rn-1=rn∙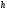 n+0,
где
n+0,
где
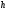 n
–многочлен из
n
–многочлен из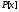 .
.
Теорема 10.2.Последний ненулевой остаток в алгоритме Евклида для ненулевых многочленов равен их наибольшему делителю.
Следствие.Для любых ненулевых
многочленов из
из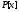 существуют
существуют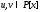 такие, что
такие, что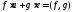 (линейное выражение наибольшего общего
делителя двух ненулевых многочленов
из
(линейное выражение наибольшего общего
делителя двух ненулевых многочленов
из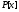 ).
).
Определение. Многочлены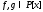 называютсявзаимно простыми, если
называютсявзаимно простыми, если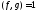 ,
т.е. общими делителями этих многочленов
могут быть только ненулевые элементы
поля
,
т.е. общими делителями этих многочленов
могут быть только ненулевые элементы
поля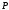 .
.
Теорема 11.2. (Основные свойства взаимной простоты).
1) Многочлены
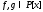 взаимно просты тогда и только тогда,
когда существуют многочлены
взаимно просты тогда и только тогда,
когда существуют многочлены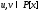 такие, что
такие, что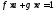 .
.
2) Если многочлены
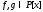 взаимно простые и
взаимно простые и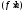 ⋮
⋮ ,
то
,
то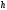 ⋮
⋮ для любого многочлена
для любого многочлена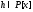 .
.
Определения. Многочлен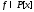 степени большей или равной 1 называетсяприводимымнад полем
степени большей или равной 1 называетсяприводимымнад полем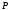 ,
если существуют многочлены
,
если существуют многочлены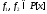 такие, что
такие, что
1)
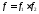 и 2)
и 2)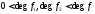 .
.
Многочлен
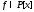 степени большей или равной 1 называетсянеприводимымнад полем
степени большей или равной 1 называетсянеприводимымнад полем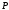 ,
если его нельзя представить в виде
,
если его нельзя представить в виде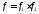 ,
где 1)
,
где 1)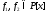 и
и
2)
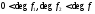 .
.
Пример 19.1) Многочлен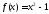 приводим над полями
приводим над полями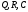 .
2) Многочлен
.
2) Многочлен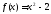 приводим над полями
приводим над полями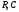 ,
но неприводим над полем
,
но неприводим над полем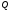 .
3) Многочлен
.
3) Многочлен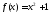 приводим над полем
приводим над полем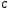 ,
но неприводим над полями
,
но неприводим над полями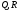 .
.
Замечания. 1) Многочлены, являющиеся
элементами поля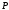 (т.е. многочлены нулевой степени и нулевой
многочлен), не являются ни приводимыми,
ни неприводимыми. 2) Многочлен первой
степени неприводим над любым полем,
содержащим его коэффициенты. 3) Многочлен
второй степени из
(т.е. многочлены нулевой степени и нулевой
многочлен), не являются ни приводимыми,
ни неприводимыми. 2) Многочлен первой
степени неприводим над любым полем,
содержащим его коэффициенты. 3) Многочлен
второй степени из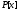 приводим над полем
приводим над полем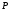 тогда и только тогда, когда его корни
лежат в поле
тогда и только тогда, когда его корни
лежат в поле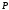 .
4) Многочлен третьей степени из
.
4) Многочлен третьей степени из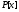 приводим над полем
приводим над полем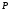 тогда и только тогда, когда хотя бы один
его корень лежит в поле
тогда и только тогда, когда хотя бы один
его корень лежит в поле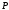 .
.
Теорема 12. 2. (Свойства неприводимости).
Если
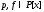 ,
,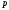 неприводим над
неприводим над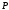 и
и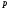 ⋮
⋮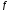 ,
то либо
,
то либо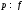 ,
либо
,
либо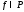 .
.Если
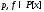 ,
,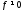 и
и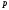 - неприводим над полем
- неприводим над полем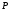 ,
то либо
,
то либо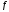 ⋮
⋮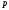 ,
либо
,
либо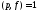 .
.Если
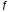 взаимно прост с многочленами
взаимно прост с многочленами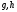 ,
то он взаимно прост и с их произведением
,
то он взаимно прост и с их произведением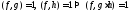 .
.Если
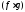 ⋮
⋮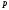 и
и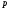 неприводим, то либо
неприводим, то либо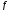 ⋮
⋮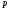 ,
либо
,
либо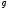 ⋮
⋮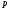 .
.Если
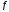 ⋮
⋮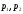 ,
где
,
где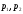 неприводимые и неассоциированные между
собой, то
неприводимые и неассоциированные между
собой, то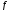 ⋮
⋮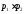 ,
т.е. и на их произведение.
,
т.е. и на их произведение.
Теорема 13.2. Всякий многочлен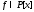 степени больше или равной 1 либо неприводим
над
степени больше или равной 1 либо неприводим
над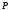 ,
либо разлагается в произведение
неприводимых над
,
либо разлагается в произведение
неприводимых над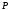 многочленов, причём это разложение
единственно с точностью до ассоциированности
и порядка следования сомножителей.
многочленов, причём это разложение
единственно с точностью до ассоциированности
и порядка следования сомножителей.





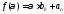
 0
0