
- •Содержание дисциплины
- •Тема 1. Краткие сведения из теории чисел
- •2. Наибольший общий делитель (нод). Алгоритм Евклида.
- •4.Взаимно простые числа. Наименьшее общее кратное (нок).
- •5. Простые и составные числа. Основная теорема арифметики.
- •7. Целые систематические числа.
- •8. Конечные и бесконечные десятичные дроби.
- •10. Решение уравненияв целых числах для целых чисел.
- •11. Признаки делимости.
- •Тема 2. Краткие сведения из алгебры многочленов
- •4. Деление с остатком в . Схема Горнера.
- •5. Наибольший общий делитель. Взаимная простота и неприводимость.
- •6. Многочлены над полем комплексных чисел .
- •7. Многочлены над полем действительных чисел.
- •8. Многочлены над полем рациональных чисел .
- •9. Нахождение рациональных корней многочленов с рациональными коэффициентами.
- •10. Освобождение от алгебраической иррациональности в знаменателе.
- •11. Симметрические многочлены и их применение.
- •Вариант 1
- •Вариант 2
- •Вариант 3
- •Вариант 4
- •Вариант 5
- •Вариант 6
- •Вариант 7
- •Вариант 8
- •Вариант 9
- •Вариант 10
- •Вариант 11
- •Вариант 12
- •Вариант 13
- •Вариант 14
- •Вариант 15
5. Простые и составные числа. Основная теорема арифметики.
Определение. Натуральное числоpназываетсяпростым,еслиp>1иpне имеет натуральных делителей, отличных от1иp.
Натуральное число nназываетсясоставным,еслиn>1иnимеет по крайней мере один натуральный делитель, отличный от1иp.
Число 1не является ни простым, ни составным.
Замечание.В школьном курсе математики
при определении простого и составного
числа обычно «забывают» упомянуть, что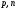 - натуральные и большие единицы. При
этом не упоминают и о натуральности
делителей, так как в школе все делители
натуральные.
- натуральные и большие единицы. При
этом не упоминают и о натуральности
делителей, так как в школе все делители
натуральные.
Теорема 7.1.(Об основных свойствах простых чисел).
1)Любое натуральное число n>1делится хотя бы на одно простое число.
2)Если простое число pделится на натуральное числоn, то либоn=1, либоn=p.
3)Если произведение целых чисел делится на простое число p, то хотя бы один из сомножителей делится наp.
4)Если натуральное число n>1является составным, то его наименьший
простой делитель не превосходит числа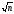 .
.
5)Если натуральное число nне делится ни на одно простое числоp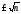 ,
тоn- простое.
,
тоn- простое.
Пример 3. Докажите, что число 127 простое.
Действительно, 127 – натуральное число,
большее 1. Кроме того, 11<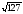 <12
и 127 не делится ни на одно простое числоp, гдеp=2,3,5,7; 11<p<12. Значит,
по свойству 5 теоремы 7.1, число 127 –
простое.
<12
и 127 не делится ни на одно простое числоp, гдеp=2,3,5,7; 11<p<12. Значит,
по свойству 5 теоремы 7.1, число 127 –
простое.
Теорема 8.1. (Основная теорема арифметики). Всякое натуральное числоn, большее единицы, либо просто, либо может быть представлено, причём единственным образом, в виде произведения простых чисел с точностью до порядка следования сомножителей.
Определение. Представление
натурального числаn>1в видеn=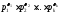 ,
где
,
где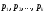 -
различные простые числа,
-
различные простые числа,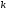 -неотрицательное
целое число, а
-неотрицательное
целое число, а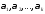 -
натуральные числа, называетсяканоническим
разложением числа.
-
натуральные числа, называетсяканоническим
разложением числа.
Следствие.Каждое натуральное числоn>1может быть представлено, причём единственным образом с точностью до порядка следования сомножителей, в каноническом виде.
Процесс представления числа n>1в канонической форме называетсяфакторизацией. Общий метод факторизации
заданного числа заключается в том, что
числоnпробуют делить
последовательно на простые числа 2, 3,
5,…,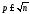 до тех пор, пока не найдётся простое
числоpтакое, чтоn⋮p.
Если такоеpнайдётся,
то дальнейшая факторизация числа
до тех пор, пока не найдётся простое
числоpтакое, чтоn⋮p.
Если такоеpнайдётся,
то дальнейшая факторизация числа сводится к факторизации числаn1=
сводится к факторизации числаn1=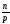 ,
меньшегоn. Если же
среди всех указанных выше простых чисел
нет ни одного делителя числаn,
то, согласно свойству 5 теоремы 7.1, само
числоnпростое,n=p1
иn=p
,
меньшегоn. Если же
среди всех указанных выше простых чисел
нет ни одного делителя числаn,
то, согласно свойству 5 теоремы 7.1, само
числоnпростое,n=p1
иn=p .
.
Пример 4. Представить в канонической
форме (каноническом виде) натуральное
число =5929.
=5929.
Перебираем по порядку все простые числа 2, 3, 5 и т.д. и ищем среди них наименьший простой делитель числа 5929. По признакам делимости на 2, 3, 5 число 5929 на них не делится. А 5929=7∙847=7∙n1. Числоn1 не делится на 2, 3, 5, поэтому делим его вновь на 7: 847=7∙121=7∙n2;n2не делится на 2, 3, 5, 7. Поэтому делимn2на следующее простое числоp=11: 121=11∙11. Таким образом,n=7∙n1=7∙7∙n2=7∙7∙11∙11=72∙112.
Теорема 9.1.(О распределении простых чисел в натуральном ряду).
1) (Теорема Евклида). Множество всех простых чисел бесконечно.
2) В натуральном ряду есть сколь угодно длинные интервалы, не содержащие простых чисел.
Теорема 10.1.(Решето Эратосфена).
1) Если во множестве натуральных чисел 2, 3, 4, 5, … n, зачеркнуть все числа, кратные первымrпростым числам 2, 3, 5, …,pr, то первое (наименьшее) не зачёркнутое число будет простым.
2) Если в этом множестве вычеркнуть все
числа, кратные всем простым до
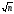 (т.е. выбратьrтак,
чтобыpr≤n<pr+1),
то оставшиеся не вычеркнутыми числа
совпадают со множеством всех простых
чиселpтаких, чтоn≥p>
(т.е. выбратьrтак,
чтобыpr≤n<pr+1),
то оставшиеся не вычеркнутыми числа
совпадают со множеством всех простых
чиселpтаких, чтоn≥p>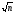 .
.
Данная теорема даёт следующий алгоритм
нахождения всех простых чисел в интервале
от 2доn: во множестве2, 3, 4, 5, …, n- первое
число2простое. Запоминаем2и
вычёркиваем все числа, кратные2.
Тогда первое не вычеркнутое число3–простое. Запоминаем3и
вычёркиваем из оставшихся все числа,
кратные3. Следующее первое не
вычеркнутое число5–простое
и т.д. Продолжаем этот процесс до простого
числаprвключительно, гдеpr≤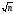 <pr+1.
Все оставшиеся не вычеркнутыми числа
образуют множество всех простых чисел,
лежащих между
<pr+1.
Все оставшиеся не вычеркнутыми числа
образуют множество всех простых чисел,
лежащих между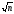 иn(включая иn,
если оно простое, т.е. не вычеркнуто). А
вместе с запомненными ранее простыми
числами 2, 3, 5, …,prполучится множество всех простых чисел,
не превосходящих числаn.
иn(включая иn,
если оно простое, т.е. не вычеркнуто). А
вместе с запомненными ранее простыми
числами 2, 3, 5, …,prполучится множество всех простых чисел,
не превосходящих числаn.
Теорема 11.1.(Применение канонической формы).
Если n=
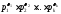 - каноническая форма натурального числаn, то все натуральные
делители числаnимеют
видc=
- каноническая форма натурального числаn, то все натуральные
делители числаnимеют
видc=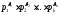 ,
где
,
где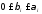 ,
,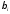 -целые
числадля всехi=1,
2, …, k.
-целые
числадля всехi=1,
2, …, k.
2) Если a,b-натуральные
числа, причёмa=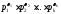 ,b=
,b=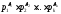 ,
гдеp1, p2,
…,pk–различные
простые числа, а
,
гдеp1, p2,
…,pk–различные
простые числа, а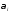 ≥0,
≥0,
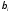 ≥0-целые
числа (согласованное представление
натуральных чиселaиb), то (a,b)=
≥0-целые
числа (согласованное представление
натуральных чиселaиb), то (a,b)=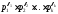 ,
где
,
где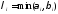 для всех
для всех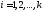 ;
[a,b]=
;
[a,b]=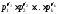 ,
где
,
где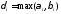 для всех
для всех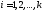 .
.
Замечание. Данные формулы обосновывают известные школьные способы нахождения НОД и НОК натуральных чисел.
6. Числовые функции.
Числовые функции– это функции, заданные на множестве всех натуральных чиселNи связанные с арифметической природой натуральных чисел.
Определение.
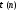 –количество всех натуральных делителей
натурального числаn.
–количество всех натуральных делителей
натурального числаn.
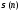 -сумма всех натуральных делителей числаn, взятых ровно по
одному разу.
-сумма всех натуральных делителей числаn, взятых ровно по
одному разу.
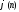 -количество всех натуральных чисел, не
превосходящихnи
взаимно простых с числомn.
-количество всех натуральных чисел, не
превосходящихnи
взаимно простых с числомn.
Функция
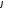 называетсяфункцией Эйлера.
называетсяфункцией Эйлера.
Пример 5.Вычислить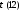 ,
,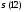 ,
,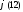 .
.
Так как 12⋮1, 2, 3, 4, 6, 12
– все натуральные делители числа 12.
Поэтому
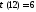 ,
,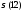 =1+2+3+4+6+12=28.
Натуральные числа 1, 5, 7, 11 и только они
не превосходят 12 и взаимно просты с 12.
Значит,
=1+2+3+4+6+12=28.
Натуральные числа 1, 5, 7, 11 и только они
не превосходят 12 и взаимно просты с 12.
Значит,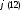 =4.
=4.
Теорема 12.1.Пусть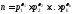 - каноническое разложение числа
натурального числаn>1.
Тогда
- каноническое разложение числа
натурального числаn>1.
Тогда
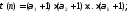
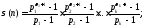
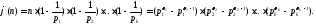
Определение. Целой частьюдействительного числаαназывается наибольшее целое числоkтакое, что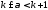 .Дробной частью– разность междуαи целой частьюα.
.Дробной частью– разность междуαи целой частьюα.
Обозначения.
 – целая часть числаα;
– целая часть числаα;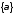 - дробная часть числаα.
Итак, [α]– целое
число и
- дробная часть числаα.
Итак, [α]– целое
число и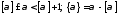 .
.
Пример 6.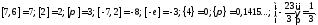
Следствия. 1) Для любых натуральных
чисел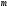 и
и количество натуральных чисел, кратных
количество натуральных чисел, кратных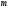 и не превосходящих
и не превосходящих ,
равно
,
равно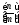 .
2) Показатель, с которым простое число
.
2) Показатель, с которым простое число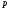 входит в каноническое разложение числа
входит в каноническое разложение числа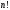 ,
равен
,
равен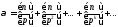 .
.
Замечание.Количество ненулевых слагаемых в данной формуле конечно.
