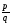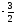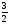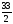- •Содержание дисциплины
- •Тема 1. Краткие сведения из теории чисел
- •2. Наибольший общий делитель (нод). Алгоритм Евклида.
- •4.Взаимно простые числа. Наименьшее общее кратное (нок).
- •5. Простые и составные числа. Основная теорема арифметики.
- •7. Целые систематические числа.
- •8. Конечные и бесконечные десятичные дроби.
- •10. Решение уравненияв целых числах для целых чисел.
- •11. Признаки делимости.
- •Тема 2. Краткие сведения из алгебры многочленов
- •4. Деление с остатком в . Схема Горнера.
- •5. Наибольший общий делитель. Взаимная простота и неприводимость.
- •6. Многочлены над полем комплексных чисел .
- •7. Многочлены над полем действительных чисел.
- •8. Многочлены над полем рациональных чисел .
- •9. Нахождение рациональных корней многочленов с рациональными коэффициентами.
- •10. Освобождение от алгебраической иррациональности в знаменателе.
- •11. Симметрические многочлены и их применение.
- •Вариант 1
- •Вариант 2
- •Вариант 3
- •Вариант 4
- •Вариант 5
- •Вариант 6
- •Вариант 7
- •Вариант 8
- •Вариант 9
- •Вариант 10
- •Вариант 11
- •Вариант 12
- •Вариант 13
- •Вариант 14
- •Вариант 15
9. Нахождение рациональных корней многочленов с рациональными коэффициентами.
Нахождение рациональных корней многочлена
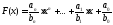 с рациональными коэффициентами (
с рациональными коэффициентами (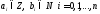 )
сводится к задаче о нахождении рациональных
корней многочлена с целыми коэффициентами,
так как
)
сводится к задаче о нахождении рациональных
корней многочлена с целыми коэффициентами,
так как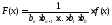 ,
где
,
где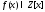 и любой корень многочлена
и любой корень многочлена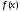 является корнем многочлена
является корнем многочлена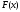 и наоборот.
и наоборот.
Нахождение рациональных корней многочлена с целыми коэффициентами.
Теорема 20.2.Пусть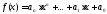 многочлен
многочлен -й
степени с целыми коэффициентами (
-й
степени с целыми коэффициентами (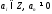 ).
Тогда несократимая рациональная дробь
).
Тогда несократимая рациональная дробь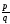 (
(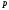 -целое,
-целое,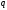 -натуральное
и
-натуральное
и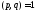 )
может быть корнем многочлена
)
может быть корнем многочлена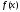 только в том случае, когда выполняются
условия: 1)
только в том случае, когда выполняются
условия: 1)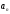 ⋮
⋮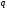 ,
2)
,
2)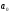 ⋮
⋮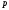 и 3)
и 3)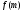 ⋮
⋮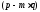 для любого целого числа
для любого целого числа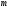 .
.
Замечание.Если для некоторой
несократимой рациональной дроби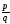 не выполняется хотя бы одно из трёх
условий теоремы, то эта дробь не является
корнем данного многочлена. Если же для
этой дроби выполняются условия 1) и 2) и
не находится целого числа
не выполняется хотя бы одно из трёх
условий теоремы, то эта дробь не является
корнем данного многочлена. Если же для
этой дроби выполняются условия 1) и 2) и
не находится целого числа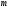 ,
для которого условие 3) не выполняется,
то нужно эту дробь непосредственно
подставить в многочлен для проверки
условия
,
для которого условие 3) не выполняется,
то нужно эту дробь непосредственно
подставить в многочлен для проверки
условия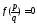 .
Количество несократимых рациональных
дробей с выполнением условий 1) и 2)
теоремы конечно. Значит, проверив их на
выполнение условия 3) частично и условия
.
Количество несократимых рациональных
дробей с выполнением условий 1) и 2)
теоремы конечно. Значит, проверив их на
выполнение условия 3) частично и условия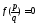 ,
можно за конечное число шагов найти все
рациональные корни данного многочлена.
,
можно за конечное число шагов найти все
рациональные корни данного многочлена.
Алгоритм нахождения рациональных
корней многочлена
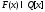 .
.
Редукция от
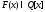 к
к .
.Находим
 многочлена
многочлена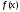 и все
и все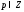 и
и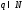 такие, что 1)
такие, что 1)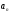 ⋮
⋮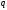 ,
2)
,
2)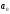 ⋮
⋮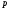 .
Исключаем среди дробей
.
Исключаем среди дробей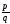 сократимые.
сократимые.Находим
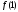 и
и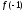 и проверяем выполнение условий
и проверяем выполнение условий ⋮
⋮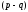
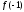 ⋮(
⋮(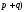 .
.Для некоторых целых чисел
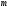 находим значения
находим значения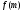 и проверяем выполнение условия
и проверяем выполнение условия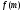 ⋮
⋮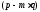 (пункты 3 и 4 нужны для отсеивания лишних
претендентов на роль рациональных
корней многочлена
(пункты 3 и 4 нужны для отсеивания лишних
претендентов на роль рациональных
корней многочлена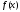 ).
).Оставшиеся не отсеянными на роль корней дроби проверяем на выполнение условия
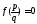 .
Полученные корни и являются искомыми.
.
Полученные корни и являются искомыми.
Пример 21. Найти рациональные корни
многочлена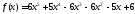 .
.
Данный многочлен имеет целые коэффициенты.
Имеем
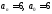 .
Так как необходимо
.
Так как необходимо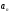 ⋮
⋮ ,
,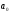 ⋮
⋮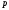 ,
то 6⋮
,
то 6⋮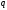 и 6⋮
и 6⋮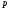 .
Значит,
.
Значит,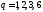 и
и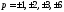 .
Поэтому
.
Поэтому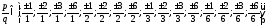 .
.
В этом множестве есть сократимые, т.е.
не взаимно простые дроби. При решении
их нужно исключить. Решение оформляем
в виде таблицы, в клеточках которой,
соответствующих дроби
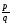 ,
ставим 0, если дробь является корнем
,
ставим 0, если дробь является корнем ,
и
,
и в противном случае. В нашей заготовке
сразу исключим из рассмотрения сократимые
дроби.
в противном случае. В нашей заготовке
сразу исключим из рассмотрения сократимые
дроби.
|
|
-1 |
1 |
-2 |
2 |
-3 |
3 |
-6 |
6 |
|
1 |
|
|
|
|
|
|
|
|
|
2 |
|
|
- |
- |
|
|
- |
- |
|
3 |
|
|
|
|
- |
- |
- |
- |
|
6 |
|
|
- |
- |
- |
- |
- |
- |
Теперь только дроби, соответствующие
незаполненным клеточкам в таблице и
только они, могут быть рациональными
корнями многочлена
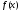 .
.
Вычисляем
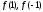 по схеме Горнера.
по схеме Горнера.
|
|
6 |
5 |
-6 |
-6 |
-5 |
6 |
|
1 |
6 |
11 |
5 |
-1 |
-6 |
0 |
|
-1 |
6 |
-1 |
-5 |
-1 |
-4 |
10 |
Значит,
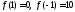 .
1 – корень
.
1 – корень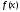 ,
-1 не является корнем. Поэтому можно
проверять лишь выполнение условия
,
-1 не является корнем. Поэтому можно
проверять лишь выполнение условия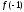 ⋮
⋮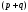 или 10⋮
или 10⋮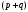 .
.
Заметим, что дробь
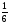 не является корнем
не является корнем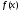 ,
так как для неё
,
так как для неё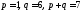 и 10 не делится на 7. Аналогично исключаем
дроби:
и 10 не делится на 7. Аналогично исключаем
дроби: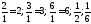 .
.
Далее находим
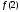 :
:
|
|
6 |
5 |
-6 |
-6 |
-5 |
6 |
|
2 |
6 |
17 |
28 |
50 |
95 |
196 |
Итак,
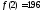 и, используя свойство
и, используя свойство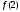 ⋮
⋮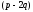 ,
исключаем дополнительно дроби:
,
исключаем дополнительно дроби: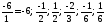 .
.
Оставшиеся дроби
 проверяем по схеме Горнера.
проверяем по схеме Горнера.
|
|
6 |
5 |
-6 |
-6 |
-5 |
6 |
|
-2 |
6 |
-7 |
8 |
-22 |
-39 |
≠0 |
|
-3 |
6 |
-13 |
33 |
-105 |
310 |
≠0 |
|
|
6 |
-4 |
0 |
-6 |
4 |
0 |
|
|
6 |
14 |
15 |
|
|
≠0 |
|
|
6 |
3 |
-7 |
|
|
≠0 |
|
|
6 |
9 |
0 |
-6 |
-9 |
0 |
Итак, рациональными корнями данного
многочлена
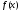 являются числа 1;
являются числа 1;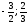 .
.