математика ГМУ ЗАО

Тема 3.2 Основные теоремы о дифференцируемых функциях и их приложения. Выпуклость функции. Основные теоремы дифференциального исчисления: теорема Ферма, теорема Ролля, теорема Лагранжа. Правило Лопиталя. Возрастание и убывание функции. Экстремумы функции. Наибольшее и наименьшее значение функции на отрезке. Выпуклость функции. Точки перегиба. Асимптоты графика функции. Общая схема исследования функции и построение их графиков. Приложение производной в экономической теории. [1,4,9] С помощью производных можно эффективно исследовать функции на возрастание и убывание, определять экстремумы функций [1,с.216,217], наибольшее и наименьшее значение. Для этого необходимо знать теоремы о достаточных условиях возрастания и убывания функции, определения точек минимума и максимума, первое и второе достаточное условие экстремума, определение выпуклости и вогнутости функции (выпуклости вниз). Необходимо знать общую схему исследования функции. В учебном пособии приведена схема исследования функции для нахождения характерных точек и особенностей, по которым можно построить ее график [1, с. 232].

Раздел 4 Интегральное исчисление. При изучении материала данного раздела студенту необходимо, прежде всего, разобраться в принципиальном вопросе: интегральное исчисление решает обратную задачу— нахождение самой функции по ее производной. Эта задача является более сложной по сравнению с задачей дифференцирования.

Тема 4.1 Неопределенный интеграл. Первообразная функция и неопределенный интеграл. Свойства неопределенного интеграла. Интегралы от основных элементарных функций. Метод замены переменной. Метод интегрирования по частям. Интегрирование простейших рациональных дробей. Интегрирование некоторых видов иррациональностей. Интегрирование тригонометрических функций [1,7]. Понятие первообразной функции [1,с.251] связывается геометрической интерпретацией, когда первообразные отличаются на число (константу). Отсюда следует определение неопределенного интеграла, как «совокупность всех первообразных для функции f(x) на промежутке Х (ось абсцисс)».

f(x)dx=F(x)+C, f(x)—подинтегральная функция, f(x)dx— подынтегральное выражение, F(x)—первообразная функция, 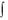– знак интеграла, С— константа.

Следует изучить свойства (с доказательствами) неопределенного интеграла (1, с.253, 254), знать табличные интегралы [1, с.255]. Обратить внимание на свойство 2 [1, с.253]: дифференциал неопределенного интеграла равен подынтегральному выражению d( f(x)dx)=f(x)dx, то есть операции интегрирования и дифференцирования взаимнообратны (знаки d и взаимно уничтожают друг друга).

Дифференциал функции y=d f(x)dx dx=d(d f(x)dx)=( f(x)dx) dx=f(x)dx.

Непосредственное интегрирование предполагает [1, примеры 1.10—10.3, с.255—257] сведение интегралов к табличным за счет тождественных преобразований и основных правил интегрирования.

21

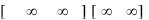
Если интеграл, полученный после замены переменной, стал «проще» данного (преобразован в табличный или приводящийся к табличному), то цель подстановки достигнута. После интегрирования функции по переменной t необходимо вернуться к прежней переменной х, выразив t через х по формуле, применявшейся при подстановке.

Примеры различных подстановок даны в [1]. Практическое применение формулы интегрирования по частям [1, с. 263], если оно целесообразно, связано с проблемой правильного разбиения подынтегрального выражения на сомножители u и dv. Отметим, что формулу интегрирования по частям, как правило, удобно применять, если подынтегральная функция является произведением многочлена

Тема 4.2 Определенный интеграл. Понятие определенного интеграла, его геометрический и экономический смысл. Свойства определенного интеграла. Определенный интеграл как функция верхнего предела. Формула Ньютона-Лейбница. Замена переменной и формула интегрирования по частям в определенном интеграле. Геометрические приложения определенного интеграла. Несобственные интегралы. Приближенные вычисления определенных интегралов. Использование понятия определенного интеграла в экономике [4]. Студенту необходимо рассмотреть задачу о площади криволинейной трапеции и разобраться в том, что площадь криволинейной трапеции есть предел площади S под ломанной в предложении неограниченного приближения ломанной к заданной кривой. Важно разобраться с понятием интегральной суммы, ее геометрическим смыслом и перейти к понятию определенного интеграла [1, с.283—285]. Студент должен знать, что в отличие от неопределенного интеграла, который является семейством кривых, определенный интеграл является числом и определенный интеграл вычисляется формулой Ньютона-Лейбница. Благодаря этой формуле, интеграл вычисляется путем нахождения приращения первообразной для данной функции на отрезке интегрирования. Достаточное условие интегрируемости функции на отрезке— непрерывность функции на этом отрезке. Студент должен разобраться в методах интегрирования, изучив для этого свойства определенного интеграла и теорему о среднем [1, с.289—291]. Метод интегрирования по частям позволяет расширить класс интегрируемых функций за пределы табличных интегралов [1, с. 241—245]. При этом необходимо использовать приемы интегрирования по частям для неопределенного интеграла. Метод подстановки также расширяет класс интегрируемых функций. При этом нужно помнить, что при введении новой переменной изменяются пределы интегрирования. После их изменения можно рассчитать определенный интеграл, не возвращаясь к старой переменной [1, пример 11.4], [2,с.259]. Для вычисления площадей плоских фигур необходимо уметь определять пределы интегрирования, если они не заданы и если площадь фигуры представляется в виде сумм или разностей криволинейных трапеций. Поэтому нужно построить кривые, ограничивающие плоские фигуры, определяют граничные условия (пределы интегрирования). Необходимо разобрать примеры [1,11.5—11.7, 11.20—11.22,

с.300—304, 313), (2, с.261, примеры 11.30—11.35].

Тема 4.3 Несобственные интегралы. Несобственные интегралы. Приближенные вычисления определенных интегралов. Использование понятия определенного интеграла в экономике [2,8]. Несобственный интеграл вычисляется как интеграл с одним или с двумя неограниченными пределами. Подынтегральная функция определена и непрерывна на одном из промежутков a;+ ),(- ;b , - ;+ . Если несобственный интеграл сходится, то он имеет конечный предел, если не сходится, то предел его равен бесконечности [2, с.271, 272]. Формула трапеций применяется для приближенного вычисления определенного интеграла, когда соответствующая первообразная не является.

22

Раздел 5 Функции нескольких переменных. При изучении темы раздела 5 необходимо проводить сравнение с функциями одной переменной и по аналогии определять область определения, но только множеством точек плоскости, а также графики в виде поверхности в пространстве [1, пример 15.2, с.400].

Тема 5.1 Точечные множества в N – мерном пространстве. Функции нескольких переменных, их непрерывность. Основные понятия. Предел и непрерывность. Свойства функций нескольких переменных, непрерывность функций нескольких переменных [4,8]. При изучении темы необходимо проводить сравнение с функциями одной переменной и по аналогии определять область определения, но только множеством точек плоскости, а также графики в виде поверхности в пространстве [1, пример 15.2, с.400].

Тема 5.2 Производные и дифференциалы функции нескольких переменных. Частные производные. Дифференциал функции. Производная по направлению. Градиент. Экстремум функции нескольких переменных. Наибольшее и наименьшее значение функции. Полный дифференциал функции. Применение дифференциала функции к приближенным вычислениям. Понятие об эмпирических формулах [6]. Техника дифференцирования функции двух переменных включает те же правила и принципы, которые использовались для нахождения производных функций одной переменной [1, пример 15.7,15.8, с.405—406]. При определении частной производной необходимо использовать понятие частного приращения.

Раздел 6 Теория вероятностей. При изучении тем этого раздела студенты сталкиваются с такими фундаментальными понятиями, как испытание (опыт, эксперимент), случайное событие, вероятность события и др. Необходимо четко представлять, что событие - это не какое-нибудь происшествие, а лишь возможный исход (результат) испытания, т.е. выполнения определенного комплекса условий.

Тема 6.1 Сущность и условия применимости теории вероятностей. Основные

перестановки (без повторений и с повторениями). Понятия и частоты событий. Свойства относительной частоты. Частные определения вероятности. Аксиоматическое определение вероятности. Классическое определение вероятности. Вероятное пространство. Теорема сложения вероятностей. Статистическая вероятность. Теорема умножения вероятностей (зависимых и независимых событий). Формула Бернулли. Формула Пуассона. Локальная и интегральная формулы Муавра-Лапласа [3]. Вероятность события есть численная мера степени объективной возможности наступления события. Если при классическом определении вероятность события определяется как доля случаев, благоприятствующих данному событию, то при статистическом определении - как доля тех фактически произведенных испытаний, в которых это событие появилось. При этом предполагается, что число испытаний достаточно велико, а события - это исходы тех испытаний', которые могут быть воспроизведены неограниченное число раз при одном и том же комплексе условий, и обладают устойчивостью относительных частот. Студент должен четко усвоить основные операции над событиями – их сумму и произведение. Если (А + В) - событие, состоящее в появлении хотя бы одного из данных событий (т.е. наступления либо события А, либо события В, либо обоих событий вместе), то АВ представляет событие, состоящее в совместном появлении двух событий (т.е. наступления и события А, и события В). Нужно знать, что событием, противоположным сумме нескольких событий, является произведение противоположных событий. Основными теоремами данной темы являются теоремы слежения и умножения вероятностей. Следует четко знать, что вероятность суммы событий равна сумме их вероятностей (т.е. Р(А + В) = Р(А) + Р(В)) для несовместных событий, а вероятность произведения событий равна произведению вероятностей (т.е. Р(АВ) = Р(А)Р(В)) для независимых событий.

23

Особое внимание следует уделить задачам по данной теме. Решение каждой из них должно сопровождаться предварительным логическим анализом условия, формулировкой и обозначением искомого события, выявлением его логической связи с другими, более простыми событиями. Этот анализ выявит применимость в данной задаче той или иной формулы или теоремы (теорем сложения, умножения, формул полной вероятности, и т.п.) и позволит обосновать дальнейшие операции, связанные с расчетом вероятностей.

При решении задачи прежде всего необходимо ввести обозначения для событий и по данным условия составить соотношения между ними, позволяющие определить искомую - вероятность через данные или более просто определяемые вероятности. Нужно соблюдать условие применимости используемой теоремы (например, условие несовместности событий при использовании теоремы сложения, условие зависимости или независимости событий при использовании теоремы умножения и т.п.).

В этой теме также рассматривается схема Бернулли – п последовательных независимых испытаний, в каждом из которых событие А может наступить с постоянной вероятностью Р(А) = р. Результат испытаний - появление т раз события А, которое чередуется в любом порядке с п-т раз не появлением события А.

При решении задач темы следует уяснить, что нужно понимать под испытанием и событием А. Далее необходимо сформулировать вопрос задачи в виде условий, налагаемых на число т наступлений события или частость (относительную частоту) m/n. Затем перейти к записи условий задачи в терминах и обозначениях схемы повторных испытаний, к выбору подходящей расчетной формулы и вычислительной схемы b.

Расчет вероятностей можно производить по точной формуле Бернулли (если п - небольшое число) и по асимптотическим формулам (если п велико).

Тема 6.2 Случайные величины и способы их описания. Понятие случайной величины. Закон распределения дискретной случайной величины. Математические операции над случайными величинами. Математическое ожидание дискретной случайной величины. Дисперсия дискретной случайной величины. Функция распределения случайной величины. Непрерывные случайные величины. Плотность вероятности. Мода и медиана. Квантили. Моменты случайных величин. Асимметрия и эксцесс [4]. В этой теме рассматривается одно из фундаментальных понятий теории вероятностей — понятие случайной величины. Под случайной величиной понимается переменная, которая в результате испытания в зависимости от случая принимает одно из возможного множества своих значений (какое именно заранее неизвестно). Если говорить более строго, то случайная величина есть функция, заданная на множестве элементарных исходов.

Наиболее полным описанием случайной величины является ее закон распределения, то есть всякое соотношение, устанавливающее связь между возможными значениями случайной величины и соответствующими им вероятностями.

При решении задач случайная величина, как и случайное событие, подлежит четкому определению по условию. Ее связь со случайным событием заключается в том, что принятие ею некоторого числового значения (т.е. выполнение равенства X = xi) есть случайное событие, характеризуемое вероятностью Р(Х = хi) = рi.

Особое внимание следует обратить на числовые характеристики случайной величины, призванные в сжатой форме выразить наиболее существенные черты распределения, в частности на математическое ожидание и дисперсию, и их свойства.

Функция распределения случайной величины - одно из фундаментальных понятий теории вероятностей, поскольку является универсальным описанием любой случайной величины. Функция распределения Р(х) представляет вероятность того, что случайная величина X примет значение, меньшее

24

х, т.е. Р(х) = Р(Х < х). Необходимо знать свойства функции распределения Р(х) и ее производной φ(х) - плотности вероятности случайной величины и уметь их изображать графически.

Тема 6.3 Модели законов распределения вероятностей, наиболее употребляемые в социально-экономических приложениях. Биноминальный закон распределения. Закон распределения Пуассона. Геометрическое распределение. Гипергеометрическое распределение. Равномерный закон распределения. Показательный (экспоненциальный) закон распределения. Нормальный закон распределения. Логарифмическинормальное распределение. Распределение некоторых случайных величин, представляющих функции нормальных величин [8].

Тема 6.4 Закон распределения вероятностей для функций от известных случайных величин. Неравенство Чебышева. Закон распределения вероятностей для функций от известных случайных величин. Неравенство Маркова (лемма Чебышева). Неравенство Чебышева. Теорема Чебышева [3,8]. Из непрерывных случайных величин особо важное значение имеет нормальный закон распределения. Необходимо знать теоретико-вероятностный смысл его параметров, выражение функции распределения РN(х) через функцию Лапласа ф(x), свойства нормально распределенной случайной величины, правило трех сигм. Важно четко представлять, что нормальный закон, в отличие от других, является предельным законом, к которому при некоторых весьма часто встречающихся условиях приводит совокупное действие (сумма) п независимых случайных величин Х1,

Х2,..., Хn при п→∞.

Тема 6.5 Закон больших чисел и его следствие. Особая роль нормального распределения: центральная предельная теорема. Закон больших чисел и его следствие. Особая роль нормального распределения. Центральная предельная теорема. Данная тема важна для понимания методов математической статистики. Она включает ряд теорем, устанавливающих при определенных условиях устойчивость частности и средней арифметической (теоремы Бернулли, Чебышева и др.). При изучении каждой из них важно уяснить условия их применимости, а также смысл утверждений, сопровождаемых словами «практически невозможно», «практически достоверно». Особое внимание следует уделить понятию «сходимость по вероятности». При использовании неравенств Маркова и Чебышева в процессе решения задач необходимо учитывать, что: 1) приведенные неравенства дают не точное значение соответствующей вероятности, а лишь ее оценку снизу или сверху (вероятность не меньше (не больше) данного числа); 2) неравенство Чебышева оценивает вероятность отклонения случайной величины X от ее математического ожидания М(Х) = а.

Тема 6.6 Цепи Маркова и их использование в моделировании социальноэкономических процессов. Определение случайного процесса и его характеристики. Основные понятия теории массового обслуживания. Понятие Марковского случайного процесса. Потоки событий. Уравнение Колмогорова. Предельные вероятности состояний. Процессы гибели и размножения. СМО с отказами [4].

Раздел 7 Математическая статистика. Прежде чем непосредственно изучать выборочный метод, необходимо ознакомиться с простейшей статистической обработкой опытных данных, построением вариационных рядов, вычислением их числовых характеристик.

Тема 7.1 Вариационные ряды и их характеристики. Вариационные ряды и их графическое изображение. Средние величины. Показатели вариации. Начальные и центральные моменты вариационного ряда [3]. Вариационный ряд является статистическим аналогом (реализацией) распределения признака (случайной величины), а его числовые характеристики - средняя арифметическая х и дисперсия s2 - аналогами соответствующих числовых характеристик случайной величины - математического ожидания М(х) и

25

дисперсии σ2. Точно так же понятие частости (относительной частости) для вариационного ряда аналогично понятию вероятности для случайной величины.

Необходимо четко знать формулы вычисления числовых характеристик ряда. Более сложные формулы, используемые в упрощенном способе расчета, являются вспомогательными и их сложность объясняется переходом в расчетах от рассматриваемых вариантов к условным.

Тема 7.2 Основы математической теории выборочного метода. Задача и её распределение. Генеральная и выборочная совокупность. Повторная и бесповторная выборка. Репрезентативная выборка. Способы отбора, применяемые на практике. Несмещенность, эффективность и состоятельность оценок. Гистограммы и полигоны частот. Статистическое распределение выборки. Эмпирическая функция распределения [4]. Выборочный метод широко применяется на практике. Однако значение этой темы значительно шире, поскольку концепция выборки лежит в основе методологии математической статистики. Соотношение между характеристиками выборочной и генеральной совокупностей есть соотношение между опытными данными (результатами наблюдений) и теоретической моделью.

Тема 7.3 Статистическое оценивание и проверка гипотез, статистические методы обработки экспериментальных данных. Статистическая гипотеза. Ошибки первого и второго рода. Виды гипотез. Статистический критерий проверки нулевой гипотезы. Критическая область. Область принятия гипотезы. Критические точки. Сравнение двух дисперсий нормальных генеральных совокупностей. Проверка гипотезы о значимости выборочного коэффициента корреляции [8]. Чтобы по данным выборки иметь возможность судить о генеральной совокупности, она должна быть отобрана случайно. Необходимо знать свойства выборочных оценок: несмешенность, состоятельность, эффективность. Уметь обосновать несмешенность и состоятельность выборочных средней и доли. При этом следует помнить, что основное требование, предъявляемое к выборочной оценке, заключается в том, чтобы ее расстояние относительно оцениваемого параметра было минимальным. Для несмещенной оценки это требование означает ее эффективность. Но даже «наилучшая» оценка является лишь приближенным значением неизвестного параметра и, будучи величиной случайной, может существенно отличаться от самого параметра. Поэтому наряду с точечной рассматривают интервальную оценку параметра, т.е. такой числовой интервал, который с заданной доверительной вероятностью (надежностью) накрывает неизвестное значение параметра. Программой предусматривается построение доверительного интервала для генеральной средней и генеральной доли собственно-случайных выборок (повторной и бесповторной). Основой являются формулы доверительной вероятности для средней и доли. Необходимо усвоить три типа задач на выборку, сводящиеся к определению предельной ошибки выборки или границ доверительного интервала, надежности оценки и объема выборки.

Если по условию задачи объем бесповторной выборки значительно меньше объема генеральной совокупности, то расчет необходимых характеристик проводят по формулам для повторной выборки.

Основными видами учебных занятий являются: лекции, практические занятия, самостоятельная работа. На лекциях в систематизированном виде излагается основное содержание тем, коренные проблемы применения математических методов для решения задач профессиональной деятельности. Целью практических занятий является закрепление, углубление и расширение знаний по рассматриваемым проблемам. В ходе практических занятий у студентов формируются умения решения задач. При организации самостоятельной работы необходимо изучить основные теоретические положения, изучая литературу по

26

математике и смежным дисциплинам, а также сформировать умения самостоятельного научного поиска и исследовательской работы. Заключительный этап изучения курса – экзамен, который проводится в два этапа:

1 этап – проверка теоретических знаний, полученных в ходе изучения дисциплины по билетам, в устной форме, с целью проверки степени усвоения обучаемыми программы курса «Математика» (либо тестирование с применением компьютера);

2 этап – проверка практических умений, полученных в ходе изучения дисциплины. Студент, успешно справившийся с первым этапом аттестации, допускается ко 2 этапу. Критерии экзаменационной оценки

1.Примерная тематика научных сообщений, рефератов

1.Применение матричного анализа в экономике.

2.Линейные операции над векторами

3.Модель Леонтьева многоотраслевой экономики (балансовый анализ).Дать экономическую интерпретацию задачи, двойственной задаче об использовании ресурсов.

4.Уравнение плоскости.

5.Линейная модель обмена.

6.Применение двойственности к однопродуктовой задаче.

7.Несимметричные двойственные задачи.

8.Геометрическая интерпретация задачи динамического программирования.

9.Принцип поэтапного построения оптимального управления.

10.Простейшие экономические задачи, решаемые методом динамического программирования.

11.Безусловная однопараметрическая оптимизация.

12.Безусловная многопараметрическая оптимизация.

13.Условная нелинейная оптимизация.

14.Применение функций в экономике.

15.Интерполирование функций.

16.Глобальные свойства непрерывных функций.

27

17.Задача о непрерывном начислении процентов.

18.Экономический смысл производной.

19.Использование понятия производной в экономике.

20.Приложение производной в экономической теории.

21.Интегрирование простейших рациональных дробей.

22.Интегрирование некоторых видов иррациональностей.

23.Интегрирование тригонометрических функций.

24.Приближенные вычисления определенных интегралов.

25.Использование понятия определенного интеграла в экономике.

26.Полный дифференциал функции.

27.Применение дифференциала функции к приближенным вычислениям.

28.Понятие об эмпирических формулах.

29.Функции нескольких переменных в экономической теории.

30.Производственные системы и теория затрат.

31.Изокоста и ее свойства.

32.Эффективное распределение ресурсов и равновесие производителя в долгосрочном периоде.

33.Функция затрат и ее свойства.

34.Функция полезности.

35.Кривые безразличия.

36.Непрерывные случайные величины.

37.Плотность вероятности.

38.Мода и медиана.

39.Квантили.

40.Моменты случайных величин.

41.Асимметрия и эксцесс.

42.Показательный (экспоненциальный) закон распределения.

43.Нормальный закон распределения.

44.Логарифмическинормальное распределение.

45.Распределение некоторых случайных величин, представляющих функции нормальных величин.

46.Особая роль нормального распределения.

47.Центральная предельная теорема.

48.Предельные вероятности состояний.

49.Процессы гибели и размножения.

50.СМО с отказами.

51.Показатели вариации.

52.Начальные и центральные моменты вариационного ряда.

53.Гистограммы и полигоны частот.

54.Статистическое распределение выборки.

55.Эмпирическая функция распределения.

56.Сравнение двух дисперсий нормальных генеральных совокупностей.

57.Проверка гипотезы о значимости выборочного коэффициента корреляции.

2.Примерные вопросы для самопроверки освоения дисциплины

28

4.Элементарными преобразованиями матрицы не являются …

1)отбрасывание нулевой строки (столбца);

2)Умножение всех элементов строки (столбца) на любое число;

3)Транспонирование матрицы;

4)Все преобразования являются элементарными.

5.Возведение матрицы А в целую положительную степень возможно лишь в случае, если …

1)А – квадратная матрица;

2)А – единичная матрица;

3)А – нулевая матрица;

4)Определитель матрицы А не равен нулю.

6.Правило Сарруса, или правило треугольников для определителей

5 0 1

29

3)элементы главной диагонали – нули;

4)нет верного ответа.

10.В матричной форме система m линейных уравнений c n переменными имеет вид А Х В , где А – матрица коэффициентов перед

неизвестными, …

Варианты ответа:

1)Х – матрица – столбец неизвестных,

В– матрица – столбец свободных членов;

2)Х – матрица – строка неизвестных,

В– матрица – строка свободных членов;

3)Х – матрица столбец неизвестных,

В– матрица строка неизвестных;

4)Х – матрица – строка неизвестных,

В– матрица – столбец свободного члена.

11.Как называется метод решения систем линейных уравнений, при котором с помощью элементарных преобразований, система уравнений приводится к равносильной системе ступенчатого или треугольного вида, из которой последовательно, начиная с последних переменных, находятся все остальные переменные?

1)Метод Крамера;

2)Метод Гаусса;

3)Метод обратной матрицы;

г) Метод элементарных преобразований.

12.Если системы имеют одно и то же множество решений, то они называются …

1) Совместными ;

2) Несовместными;

3) Равносильными;

4) Неопределенными.

13.Если система линейных уравнений имеет хотя бы одно решение, то она называется …

1) Совместной;

2) Несовместной;

30