Desktop_2 / 1 курс 1 семестр / Математика Часть1

3π

2

Рис. 6

Полученная кривая называется кардиоидой.

2. Перейдя от декартовых координат к полярным, построить линию

( x2 + y2 )2 = 25( x2 − y2 ) .

Решение

ρ4 = 25ρ2 (cos2 ϕ−sin2 ϕ) .

π

3π

2

Рис. 7 Полученная кривая называется леминискатой Бернулли.

19

Задания для контрольной работы № 1

1-10. Доказать, что данная система имеет единственное решение, найти его по формулам Крамера. Найти решение системы матричным методом.

11-20. В прямоугольной системе координат Oxyz даны точки M1 , M 2 , M 3 , M 4 . Доказать, что они не лежат в одной плоскости. Найти объем пирамиды

21-30. В условиях предыдущей задачи:

20

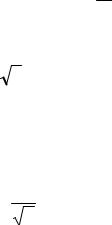
1. Написать уравнение плоскости ( α), проходящей через точки M1 , M 2 , M 3 ; 2. Найти расстояние от начала координат до плоскости ( α);

3. Записать уравнение прямой, проходящей через точку M 4 перпендикулярно плоскости ( α);

4.Найти координаты проекции точки M 4 на плоскость ( α);

5.Найти координаты точек пересечения плоскости ( α) с осями коорди-

нат.

31-40. Написать каноническое уравнение кривой, применяя метод выделения полного квадрата. Найти координаты центра кривой (для окружности, эллипса и гиперболы), координаты вершин (для параболы). Сделать чертеж.

31.5x2 − 4y2 +30x +8y + 21 = 0 .

32.9x2 +16 y 2 −18x −64 y −71 = 0 .

33.x2 +8x + y +14 = 0 .

34.4x2 + 9 y2 − 36 y = 0 .

35.x2 − y2 − 4x + 6 y − 9 = 0 .

36.y2 − 2y −3x −14 = 0 .

37.9x2 +18x −16 y 2 −135 = 0 .

38.x2 + y2 −8x + 4 y + 4 = 0 .

39.x2 − 2x −3y − 2 = 0 .

40.x2 + 4 y2 − 2x +8y −11 = 0 .

41-50. Построить кривые в полярной системе координат. Углу ϕ придавать значения с шагом, равным 12π .

21

51-60. Перейти от декартовых координат к полярным и построить линию.

22

II.ВВЕДЕНИЕ В МАТЕМАТИЧЕСКИЙ АНАЛИЗ

1.Функции и их графики

Переменная величина y называется функцией переменной величины x, если каждому значению x, взятому из некоторого множества, по определенному правилу (закону) ставится в соответствие единственное значение y. При этом х на-

зывают независимой переменной или аргументом, y – зависимой переменной или функцией. Функциональную зависимость x и y в общем виде записывают так: y=f(x). Множество допустимых для х значений называется областью определения функции D(f). Множество значений, принимаемых переменной y, называется

областью значений функции y=f(x): E(f).

Существует несколько способов задания функции. Однако наиболее часто встречаются следующие способы: аналитический, табличный и графический. Если функция задана аналитически, то есть с помощью формулы вида y=f(x), то область определения функции – это область значений переменной, допустимых

Ответ: [3 ; 4) (4 ;+∞).

Пример: Дана функция f (x) = 2x .

Найти f (0), f (2x +1), f ( 1x ), f (log2 5) . Решить уравнение

2[ f (x)]4 −17[ f (x)]2 +8 = 0 .

Решение

Далее решаем уравнение. Оно будет иметь следующий вид:

23

Во многих случаях свойства функций становятся более ясными и наглядными, если функцию изобразить графически. Графиком функции называется множество точек плоскости Оxy, координаты которых имеют вид М(х,f(x)), где

х D( f ) , а ордината – соответствующее значение функции.

Элементарной называется функция, которую можно задать одним аналитическим выражением, составленным из основных элементарных функций с помощью конечного числа арифметических действий и конечного числа операций взятия функции от функции. Следующие функции называются основными эле-

ментарными:

1. Степенная функция y = xα , где α – действительное число. Приведем графики некоторых степенных функций:

1) y=х. ( α =1 )

y

24

4) y = 1x .

( α = −1 )

5) y = x . ( α = 12 ).

2. Показательная функция y = a x , где а > 0, а ≠1 .

a>1 (y=2x) 0<a<1 (y=0,5x)

25

4) график функции y = f(kx) получается из графика функции y = f(x) путем

5) график функции y = –f(x) получается из графика функции y = f(x) путем симметричного отражения относительно оси Ox, а график функции y = f(-x) получается симметричным отражением относительно оси Oy.

С помощью этих преобразований можно построить графики многих других более сложных функций чисто геометрическим путем. Рассмотрим несколько примеров.

Примеры

Построить графики функций: 1. y = 2xx−+11 .

Решение

Преобразуем функцию следующим образом:

фика функции y = 3x путем его сдвига на 1 единицу вправо вдоль оси Ох (см. п.

2, a = 1 ) и сдвигом полученного графика вверх вдоль оси Оy на 2 единицы вверх.

Рис. 8

27

2. y = sin 2x .

Решение

Строим график функции y = sin x , далее сжимаем график по оси абсцисс в два раза, т. е. уменьшаем абсциссы точек графика в два раза, оставляя ординаты без изменения. При этом заметим, что период функции y = sin 2x равен π. Сжатие графика функции удобно проводить в характерных точках графика функции y = sin x ( 0, π2 , π, 32π, 2π и т. д.)

Рис. 9

3. y = sin2 x .

Решение

Прежде чем строить график, преобразуем данную функцию следующим образом:

График этой функции можно получить из графика функции y = cos x , выполнив последовательно такие преобразования: сжатие по оси абсцисс в два раза; сжатие по оси ординат в два раза; симметричное отражение относительно

оси абсцисс; параллельный перенос вдоль оси ординат вверх на 12 единицы масштаба. График функции y = sin2 x представлен на рис. 10.

Рис. 10

28