Федеральное агентство железнодорожного транспорта Уральский государственный университет путей сообщения Кафедра «Высшая и прикладная математика»

В. В. Башуров О. А. Башурова С. А. Ягупов

Вычислительная математика и моделирование систем

Екатеринбург Издательство УрГУПС

2012

Федеральное агентство железнодорожного транспорта Уральский государственный университет путей сообщения Кафедра «Высшая и прикладная математика»

В. В. Башуров О. А. Башурова С. А. Ягупов

Вычислительная математика и моделирование систем

Методические указания для студентов заочного обучения

по направлению подготовки бакалавров 230400 – «Информационные системы и технологии»

Екатеринбург Издательство УрГУПС

2012

УДК 519.6 Б33

Авторы: В. В. Башуров – доцент кафедры «Высшая и прикладная математика», канд. физ.-мат. наук, УрГУПС О. А. Башурова – ассистент кафедры «Высшая и прикладная математика», УрГУПС

С. А. Ягупов – доцент кафедры «Высшая и прикладная математика», канд. физ.-мат. наук, УрГУПС

Рецензент: В. Е. Замыслов – доцент кафедры «Высшая и прикладная математика», канд. физ.-мат. наук, УрГУПС

Башуров, В. В.

Б33 Вычислительная математика и моделирование систем : метод. указания / В. В. Башуров, О. А. Башурова, С. А. Ягупов. – Екатеринбург :

УрГУПС, 2012. – 51, [1] с.

Методические указания содержат краткий теоретический курс по вычислительной математике и моделированию систем. По различным темам приведены примеры решения задач с использованием математического пакета Mathcad. Предложены задания для работы на занятиях и самостоятельной работы студентов. В пособии даны задания для контрольных работ, причем последняя цифра указывает номер варианта студента.

Пособие предназначено студентам направления подготовки бакалавров230400

– «Информационные системы и технологии» для изучения дисциплин «Моделирование систем» и «Вычислительная математика».

УДК 519.6

Печатается по решению редакционно-издательским советом университета

©Уральский государственный университет путей сообщения (УрГУПС), 2012

Оглавление

Введение ……………………………………………………..…………...…….. 4

ЧАСТЬ I. МОДЕЛИРОВАНИЕ СИСТЕМ..………………………..…….…… 5

1.Погрешности вычислений ……………...………………….…………… 5

2.Решение систем линейных уравнений..……………………….…….….. 7

3.Интерполяция функций ……………….…………………..…………… 10

4.Метод наименьших квадратов ………...……………………………… 17

Задания для контрольной работы «Моделирование систем»..………..….... 26

ЧАСТЬ II. ВЫЧИСЛИТЕЛЬНАЯ МАТЕМАТИКА.……………………...… 28

5.Решение уравнений……………………………...……………………… 28

6.Численное интегрирование ……………………..……….........………... 33

7.Ряды Фурье ………………………………………..………...………..… 36

8.Численное решение дифференциальных уравнений …..……...……... 40

Задания для контрольной работы «Вычислительная математика»……...… 46

Лабораторные работы ...………….....................…………..………...………. 48

Библиографический список ………….………………………….……..…..… 51

3

Введение

Работа студента-заочника в УрГУПС предполагает самостоятельное изучение теоретического материала и выполнение практических заданий. Для этой цели служат контрольные работы, выполняемые в течение семестра.

В данном пособии содержатся теоретические сведения, методические указания и сами контрольные работы. Здесь же указана литература. Вариант контрольной работы студент выбирает в соответствии с присвоенным ему шифром (номеру варианта соответствует последняя цифра номера в зачетной книжке).

Правила выполнения контрольной работы:

1.Контрольная работа должна быть выполнена в отдельной тетради и сдана в деканат (не забудьте указать фамилию преподавателя!).

2.Работу следует оформлять в тонкой тетради, оставляя место для исправления ошибок (желательно писать на левой странице, оставляя чистой правую). Если при проверке работы в ней обнаружены ошибки, то студент должен их исправить и отослать работу вновь на проверку. Работа должна быть отправлена не позднее 2-х недель до начала сессии.

3.Решение задач должно быть достаточно подробным и логически обоснованным. Полезно в ходе решения приводить формулы, формулировки теорем или другие теоретические сведения, на основании которых делается заключение.

4.Работа может быть выполнена без привлечения математических пакетов, но приветствуется использование пакета Mathcad, а также Excel.

.

4

Часть I. Моделирование систем

1. Погрешности вычислений

На различных этапах решения задачи могут возникать погрешности, искажающие результаты вычислений. Оценка точности результатов вычислений является важнейшим этапом организации вычисления, тем более при отсутствии опытных или других данных для сравнения. Различают три типа погрешностей.

1.Математическая модель никогда во всей полноте точно не отражает описываемый объект. Кроме того, некоторые данные, входящие в математическую модель, могут иметь погрешность. Это погрешность математической модели. Она называется неустранимой погрешностью.

2.Численный метод решения задачи является источником погрешности. Возникающая при этомпогрешность численного методатеоретически может быть отрегулирована за счет изменения некоторого параметра(например, шага разбиения интервала, числа членов ряда, числа итераций). Погрешность метода обычно стараются довести до величины, в несколько раз меньше неустранимой погрешности.

3.Вычислительная погрешность связана спогрешностью округления чисел

из-за ограниченности представления чисел в компьютере. Числа в компьютере представлены в двух видах: целые и действительные. Целые числа записываются точно и действия с ними производятся точно, если возможно. Действительные

числа записываются в форме с плавающей точкой, например -1535 ×10-1 , -1,535 ×102 , -0,1535 ×103 . Последняя запись – нормализованная форма числа с плавающей точкой. Примерно так записываются числа в память компьютера. Значащими цифрами числа называются все цифры вего записи справа, начиная с первой ненулевой цифры. Для каждого типа действительных чисел в памяти компьютера выделено определенное число байтов. Поэтому при записи с плавающей точкой воспринимается только определенное количество значащих цифр, осталь-

ные отбрасываются. Таким образом, компьютер оперирует с приближенными значениями действительных чисел.

При рассмотрении приближенных чисел различают два вида погрешностей: абсолютную и относительную. Абсолютная погрешность – это разность по модулю между точным значением числа x и его приближенным значением a

Dx =x - a .

Относительная погрешность – это отношение абсолютной погрешности к приближенному значению числа (часто записывается в процентах)

δx = Dx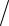 a .

5

Так как истинное значение x обычно неизвестно и имеем лишь приближенное значение a , то в качестве абсолютной погрешности используют предельную погрешность Da , которая определяется следующим образом:

–если число a получено в опыте при измерениях, то в качестве Da берут шкалу деления измерительного прибора;

–если число a получено путем округления, то в качестве Da берут половину единицы последнего разряда числа;

–при вычислении в компьютере округления не производятся, а цифры, не умещающиеся в разрядную сетку, отбрасываются. В этом случае погрешность Da

вдва раза больше по сравнению с результатом округления.

И в качестве относительной погрешности используется формула

δx = D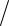a a .

Тогда любое число x можно записать через оценку в следующем виде:

При вычислениях погрешности чисел определяются по формулам:

При массовых вычислениях необходимо придерживаться следующих правил.

1.При сложении и вычитании приближенных чисел в результате следует сохранять столько десятичных знаков, сколько их в приближенном данном с наименьшим числом десятичных знаков.

2.При умножении и делении в результате следует сохранять столько значащих цифр, сколько их имеет приближенное данное с наименьшим числом значащих цифр.

6

3.При возведении в степень (в том числе дробную) в результате следует сохранять столько же значащих цифр, сколько их имеет основание.

4.Во всех промежуточных результатах длительных вычислений следует сохранять одной цифрой более, чем рекомендуют предыдущие правила. В окончательном результате эта «запасная цифра» отбрасывается.

5.Если некоторые данные имеют больше десятичных знаков(при сложении и вычитании) или больше значащих цифр (при умножении, делении или возведении в степень), чем другие, то их предварительно следует округлить, сохраняя одну лишнюю цифру.

7

Совокупность коэффициентов aij составляет квадратную матрицу A = aij .

Необходимым и достаточным условием существования единственного решения системы линейных уравнений является неравенство нулю определителя матрицы коэффициентов. В случае равенства нулю определителя матрица называется вырожденной. При этом система либо не имеет решения, либо имеет их бесконечное множество.

Одним из самых распространенных методов решения системы линейных алгебраических уравнений являетсяметод Гаусса. Он основан на приведении матрицы A коэффициентов системы к треугольному виду. Рассмотрим данный метод на примере системы трех уравнений:

a11 x1 + a12 x2 + a13 x3 = b1 ;

a21x1 + a22 x2 + a23 x3 = b2 ;

a31x1 + a32 x2 + a33 x3 = b3 .

Для исключения x1 из второго уравнения умножаем первое уравнение на

- a21 и складываем его со вторым уравнением, полученное уравнение поста-

a11

вим вместо второго. Тогда первый коэффициент полученного второго уравнения станет равным нулю. То же самое проделаем с третьим уравнением, умно-

жив исходное первое уравнение на - a31 . В результате система будет преобра-

a11

зована к следующему виду:

a11 x1 + a12 x2 + a13 x3 = b1 ; a22¢ x2 + a23¢ x3 = b2¢;

a32¢ x2 + a33¢ x3 = b3¢,

где aij¢ = aij - a1 j ×ai1 / a11 ; bi¢ = bi × ai1 / a11 , i, j = 2,3.

Теперь из третьего уравнения необходимо исключить член, содержащий

x2 . Для этого умножаем второе уравнение на- a32¢ и складываем с третьим,

a22¢

полученное уравнение поставим вместо третьего. Получим

a11 x1 + a12 x2 + a13 x3 = b1 ; a22¢ x2 + a23¢ x3 = b2¢;

8

где aij¢¢ = aij¢ - a2¢ j × a¢j 2 / a22¢ , bi¢¢= bi¢ - bi¢× ai¢2 / a22¢ , i, j = 3 .

Матрица системы приведена к треугольному виду. Такой этап называется прямым ходом метода Гаусса. Теперь из третьего уравнения можно найти x3 ,

затем подставить его во второе уравнение и найти из него x2 и т. д. (обратный ход метода Гаусса):

Пример. Методом Гаусса решить систему уравнений

ì 2,1x1 -1,3x2 + 0,6x3 = 3, 2;

ï

í1, 2x1 +1,5x2 -1,=0x3 -1,7; ïî-0,6x1 + 2,5x2 -1,3x3 = 0,5.

1, 2

Решение. Умножаем первое уравнение на - = -0,57 и складываем

2,1

его со вторым уравнением, полученное уравнение поставим вместо второго.

Умножим исходное первое уравнение на- -0, 6 = 0, 29 и складываем его с

2,1

третьим уравнением, полученное уравнение поставим вместо третьего. В результате получаем

9