выч.математика - Башуров

Рис. 14. Исходная функция с четным продолжением

иее представление через ряд Фурье

8.Численное решение дифференциальных уравнений

По определению производная функции y = f (x) вычисляется по форму-

ле

y¢ = f ¢(x) = lim Dy ,

Dx®0 Dx

где Dx – малое приращение аргумента, Dy =f (x + Dx) - f (x) – приращение

функции. Если невозможно применить аналитическую формулу, то производная аппроксимируется с помощью отношения конечных разностей Dy и Dx :

40

y¢ » Dy / Dx.

В таком случае функцию y = f (x) обычно представляют в табличном виде: y0 , y1 ,… при x = x0 , x1 … Пусть шаг – разность между соседними значе-

ниями аргумента – постоянный и равен h . Запишем выражения для производной y1 при x = x1 . В зависимости от способа вычисления конечных разностей

получаем разные формулы для вычисления производной в одной и той же точке:

стей.

Рассмотрим дифференциальное уравнение первого порядка, разрешимое относительно производной, в виде y¢ = f (x, y ) с заданным начальным условием y (x0 ) = y0 .

Необходимо найти такую функцию y = φ (x), которая удовлетворяла бы

дифференциальному уравнению и проходила через заданную точку. Такая задача носит название задачи Коши. Для некоторых типов уравнений существуют способы аналитического решения. В основном задачу приходится решать численными методами.

Наиболее распространенные численные методы решения дифференциальных уравнений – методы конечных разностей. Суть методов состоит в следующем: область непрерывного изменения аргумента и функции заменяется дискретным множеством точек, называемых узлами. Эти узлы составляют разностную сетку. Искомая функция непрерывного аргумента приближенно заменяется функцией дискретного аргумента на заданной сетке. Такая функция называется сеточной. Исходное дифференциальное уравнение заменяется разностным уравнением, т. е. производные заменяются конечно-разностными отношениями. Такая замена дифференциального уравнения разностным называ-

ется его аппроксимацией на сетке или разностной аппроксимацией.

Одним из самых простых методов являетсяметод Эйлера. Значения функции в узлах x0 , x1 … заменим сеточной функцией y0 , y1 ,… Шаг примем постоянным h = xi+1 - xi = const . Заменим производную конечно-разностным отношением:

41

найти значения функции во всех точках сетки. Точность метода порядка h . Порядок точности можно повысить путем усложнения разностной схемы.

Весьма распространены в практических вычисленияхметоды Рунге–Кутта второго и четвертого порядков точности. Вычисления по методам Рунге– Кутта второго порядка точности проводятся в два этапа. Их часто называют методами типа предиктор – корректор, потому что они работают по принципу предсказание – поправка. На первом этапе находится промежуточное значение yi+12 по формуле Эйлера с шагомh / 2, а на втором этапе строится значение

Точность метода порядка h2 . Наиболее широкое применение нашли методы Рунге–Кутта четвертого порядка

Точность метода порядка h4 . В современных вычислительных средах, как правило, используются варианты методов Рунге–Кутта с автоматическим выбором шага по независимой переменной(величина шага может изменяться в процессе интегрирования в зависимости от оценки полученной точности).

Пример. Решить дифференциальное уравнение y¢ = xy с начальным ус-

ловием y (0) = 2 численными методами, сравнить с аналитическим решением.

42

Решение. Точное решение: y = 2ex2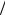2 . Рассмотрим решение на интервале

Метод Рунге–Кутта четвертого порядка:

Рис. 15. Точное и численные решения

Также дифференциальное уравнение можно приближенно решить с -по мощью представления искомой функции в виде степенного ряда (например, ряда Тейлора). Неизвестные коэффициенты ряда находятся последовательно из самого дифференциального уравнения.

43

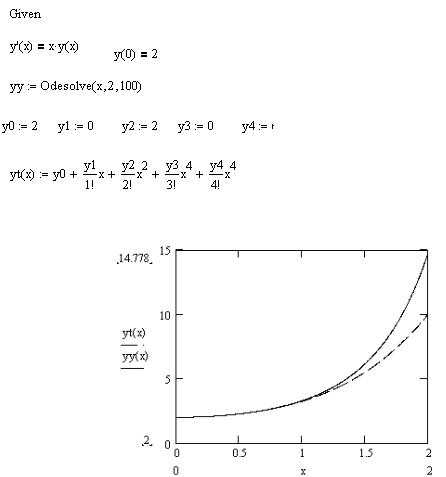
Пример. Представить решение дифференциального уравнения y¢ = xy с

начальным условием y (0) = 2 через ряд Тэйлора до четвертой степени.

Решение. Представление функции в виде ряда Тэйлора в окрестности

Сравним его с решением, полученным с помощью пакетаMathcad численным интегрированием

Изобразим решения через ряд Тейлора и численным методом (рис. 16).

Рис. 16. Численное решение дифференциального уравнения и решение в виде ряда Тейлора

44

Дифференциальные уравнения второго порядка и выше можно решить с помощью численного интегрирования или свести с помощью замен к системе дифференциальных уравнений первого порядка.

Пример. Решить с помощью пакетаMathcad дифференциальное уравнение y¢¢ - 2 y¢ + 5 y =(2t 2 - 4t )sin (2t ) с начальными условиямиy (0) = -1,

y¢(0) = 2 с помощью численного интегрирования и сведением к системе диф-

ференциальных уравнений.

Решение

Рис. 17. Решение дифференциального уравнения двумя численными методами

45

Задания для контрольной работы «Вычислительная математика»

21–30. Задачи на решение нелинейных уравнений

Найти корни уравнения аналитическим способом, округляя полученные значения до двух знаков после запятой. Найти наименьший корень методом

хорд, а наибольший – методом касательных с точностью ε =10-2 . Уравнения заданы в вариантах:

31–40. Задачи на численное интегрирование

Вычислить определенные интегралы по формалам трапеций и Симпсона с шагом h = 0,1. Интегралы приведены в вариантах:

46

41–50. Задачи на численное решение дифференциальных уравнений

Найти решение дифференциального уравнения первого порядка методом Эйлера с шагом h = 0,1 на интервале [0; 0,5]. Представить решение в виде ряда Тэйлора до четвертой степени и найти необходимые коэффициенты. Изобразить решения на чертеже. Дифференциальные уравнения с начальными данными приведены в вариантах:

47

Лабораторные работы

При изучении дисциплин«Моделирование систем» и «Вычислительная математика» полезно изучить некоторый математический пакет. Одним из доступных и понятных студентам пакетов являетсяMathcad, который позволяет решать математические задачи различной сложности. Ниже приведены лабораторные работы, которые помогут студентам освоить этот программный продукт и на пратике изучить дисциплины. Во всех вариантах стоит параметр N , который преподаватель сам определяет для студентов в группе.

Лабораторная работа 1 Система линейных алгебраических уравнений

Лабораторная работа 2 Интерполяция табличных функций

Задана табличная функция при x = 0,1, 2...10 со значениями счетчика слу-

чайных чисел rnd(N). Вычислить значение в точке x = N + 0,3 с помощью: 5

–локальной линейной интерполяции;

–сплайнов;

–глобальной интерполяции.

Построить графики табличной функции и указанных видов интерполяции.

48

Лабораторная работа 3 Метод наименьших квадратов

1.Методом наименьших квадратов найти коэффициенты линейной аппроксимирующей функции.

2.С помощью оператора linfit определить линейную, квадратическую и гиперболическую аппроксимацию.

3.Построить степенную и показательную аппроксимации.

4.Вычислить среднеквадратические отклонения всех аппроксимаций и выбрать наилучшее приближение.

Лабораторная работа 4 Решение нелинейных уравнений

1.Найти производную функции f (x) и изобразить ее вместе с функцией

графически.

2. Определить количество корней f (x) = 0 и найти их через операторroot и

блок Given-Find.

Лабораторная работа 5 Гармонический анализ

Построить разложение в ряд Фурье при10, 50 и 100 членах ряда. Изобра-

é N N ù

зить функцию и Фурье-представления на интервале ê- ; ú .

ë 3 3 û

2.Задана функция g (x) = N ×e-N ×x при 0 £ x £1. Разложить функцию по коси-

нусам в ряд Фурье при5, 10 и 50 членах ряда. Построить графики функции с четным продолжением и представление в виде ряда Фурье на интервале [-1;1].

49