
Фишбейн, механика
.pdf
Равномерное движение по окружности ( at = 0 ):
at = 0 , an = const
u = const
S = ut .
Равнопеременное движение по окружности ( at = const ):
at = const , an ¹ const u = u0=+ att u0 ± at t
|
|
|
a t 2 |
at |
t2 |
|
|
||
|
|
S = u0t + |
t= |
u0t ± |
|
|
|
. |
|
|
|
|
2 |
|
|||||
|
|
2 |
|
|
|
|
|||
Ускоренное: |
r |
r |
|
|
at |
> 0. |
|||
u at , модуль u увеличивается, |
|||||||||
Замедленное: |
r |
r |
|
|
at |
< 0. |
|||
u ¯ at , модуль u уменьшается, |
|||||||||
Вращательное движение
r
Вектор бесконечно малого угла поворота dj. Направлен вдоль оси вращения по направлению поступательного движения правого винта, если его вращать по направлению поворота(Если 1-2, то вверх, если 1-2′, то вниз). По
r r r
модулю равен углу поворота dj ³ 0 , проекция djz = ±dj. Dj =j2 - j1 - вектор конечного углового смещения или угла поворота.
|
|
|
z |
r |
|
|
|
dj |
|
|
|
|
|
r |
|
r |
2′ |
|
e |
r |
w |
d j |
r |
|
e ¯ |
|
|
d j 2 wr e ¯ |
|
r |
|
r |
1 |
|
e |
|
|
||
|
|
dj |
|
|
|
|
Угловая скорость |
r |
|
|
|
|
|
|
|
|||||
|
|
w |
|
|
|
|
|
|
|||||||
r |
|
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
dj |
. |
|
|
|
|
|
|
|
|
|
|
|
|||
w = |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
dt |
|
|
r |
|
|
|
|
|
|
r |
|||||
|
|
|
|
|
|
|
|
|
|
||||||
Вектор угловой скорости w направлен вдоль оси вращения по направлению dj, |
|||||||||||||||
w== |
djz |
±w, Dj |
|
|
|
|
t2 |
|
dt - площадь |
под кривой w |
|
от t с |
|||
z |
=j |
2 z |
- j |
= w |
z |
||||||||||
|
|||||||||||||||
z |
|
dt |
|
|
1z |
ò |
z |
|
|
|
|||||
|
|
|
|
|
|
|
t1 |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
пишут j. |
|
|
|
|||
учетом знака. Очень часто вместо |
jz |
|
|
|
|||||||||||
10

|
|
Угловое ускорение e |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
r |
|
|
r |
|
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
d 2j |
dw |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
e |
|
dt2= |
dt |
=. |
|
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r |
||||||
Вектор углового ускорения e направлен вдоль оси вращения по направлению dw. |
||||||||||||||||||||||||||||||||||||||||
e=== |
d 2jz |
|
dwz |
|
±e, Dw |
|
|
|
|
|
|
|
|
|
|
t2 |
z dt |
|
|
|
|
|
|
|
|
|
|
|
|
e |
|
|
|
|||||||
|
|
|
|
|
|
|
|
z |
w= |
2 z |
- w |
= e |
- площадь под кривой |
z |
от |
|||||||||||||||||||||||||
|
|
2 |
|
|
|
|
||||||||||||||||||||||||||||||||||
z |
|
|
dt |
|
dt |
|
|
|
|
|
|
|
1z |
ò |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
t с учетом знака. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
Угловой путь Ф |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dФ |
|
|
|
|
|
|
|
|
|
||
Ф = òwdt ³ 0 - |
|
площадь под кривойw от t , w |
|
= |
|
³ 0 -модуль угловой |
||||||||||||||||||||||||||||||||||
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dt |
|
|
|
|
|
|
|
|
|
||
скорости. |
Если вращение без изменения направления, то |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
Ф |
= |
|
|
|
r |
|
|
Dj= |
|
|
Dj |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
Dj= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Равномерное вращение точки ( e =0) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
e =0 |
|
|
|
|
|
|
|
|
|
|
ez =0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
w = const |
|
|
|
|
|
|
|
|
w= |
±w |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
Ф = wt |
|
|
|
|
|
|
|
|
|
|
jz= j0 z + wzt |
|
|
|
или Djz= wzt |
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Равнопеременное вращение точки ( e = const ) |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
e = const |
|
|
|
|
|
e |
z |
= ±e, w= |
|
±w |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0z |
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
w w=0 ± et |
|
|
|
|
wz= w0z + ezt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
Ф = w t ± |
et 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
t + |
|
|
e |
t2 |
|
|
|
|
t + |
e |
t2 |
||||||||||||
|
|
|
|
|
|
|
j |
z |
|
=j |
+ w |
|
|
|
|
z |
|
|
или Dj |
z |
=w |
|
z |
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
0 |
|
|
2 |
|
|
|
|
|
|
|
|
|
0 z |
|
0 z |
|
2 |
|
|
|
|
0 z |
|
|
2 |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
( + ) ускоренное, ( -) замедленное |
r |
|
|
|
|
|
|
|
|
|
|
e, |
r |
|
|
|
-e, |
|
|
|
|
|||||||||||||||||||
e OZ→ e = |
|
e ¯ OZ→ e= |
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
r |
|
|
|
|
|
|
|
|
z |
|
|
|
|
|
|
|
|
r |
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
¯OZ→ w0 z = -w0 . |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
w0 OZ→ w0 z = w0 , w0 |
||||||||||||||||||||||||||||
|
|
|
|
|
|
r |
|
|
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
и ez -одинаковые. |
|||||||||
Ускоренное: w e, модуль w увеличивается, знаки wz |
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
r |
|
|
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
знаки wz |
и ez -разные. |
|
|
|
|
|||||||||||
Замедленное: w ¯ e, модуль w уменьшается, |
|
|
|
|
||||||||||||||||||||||||||||||||||||
11
Связь линейных и угловых физических (в радианах) и технических (в оборотах) величин
F - угловой путь в радианах, w-угловая скорость в радианах в секунду, N -угловой путь в оборотах, v, n -угловая скорость в оборотах в секунду, S -линейный путь в метрах, u -линейная скорость в метрах в секунду,
r - радиус траектории движения точки.
F = |
S |
, |
w = |
u |
, N = |
F |
, v = n = |
w |
, |
|||||||
|
r |
|
|
|
||||||||||||
|
|
r |
|
|
|
2p |
|
2p |
||||||||
|
at |
|
= er , an = w2 r , a = r |
w4 + e2 |
. |
|||||||||||
|
|
|||||||||||||||
|
|
|
|
|
|
Плоское движение |
|
|
|
|
||||||
Плоское движение (качение |
тел) |
– сумма поступательного движения |
||||||||||||||
|
|
|
|
|
|
r |
|
|
|
|
|
|
|
|
|
|
тела со скоростью центра |
массvC |
(все |
точки тела |
движутся одинаково) и |
||||||||||||
вращательного вокруг неподвижной оси, проходящей через центр масс тела, с
|
|
r |
|
|
|
линейной скоростью u ( u = wR , R - радиус колеса, шара, цилиндра и т. д.). |
|||||
|
A |
|
|
A |
A |
|
r |
r |
|
|
|
C |
vC |
vC |
A |
r |
R |
|
|
C |
|
vC |
|
|
|
|
= |
|
+ |
|
|
|
|
|
r |
|
|
|
|
|
u |
A
|
r |
r |
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
v = vC |
+ u – результирующая скорость для любой точки тела. |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
r |
r |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
1 vC |
u |
|
v1 = vC + u |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
v4 = |
vC2 |
+ u2 |
|
|
r |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
u |
|
v4 |
|
r |
|
|
|
2 vC |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
vC |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
r |
|
|
|
|
|
|
|
|
r |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
r |
|
|
|
r |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
4 |
vC |
R |
|
u |
|
r |
v2 |
= |
2 |
+ u |
2 |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
vC |
|
|
|||||||||
|
|
|
|
|
|
|
r |
|
r |
|
|
|
|
v2 |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
u |
|
vC |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Точка |
|
|
каса |
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
v3 |
= |
|
vC - u |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Если тело движется без проскальзывания, то в точке касания опоры его скорость равна нулю, т. е. v3 = vC - u = 0, а это значит, что vC = u = wR . В
этом случае сила трения скольжения есть, а ее работа равна нулю, так как нет движения одного тела по поверхности другого.
12

Тесты с решениями
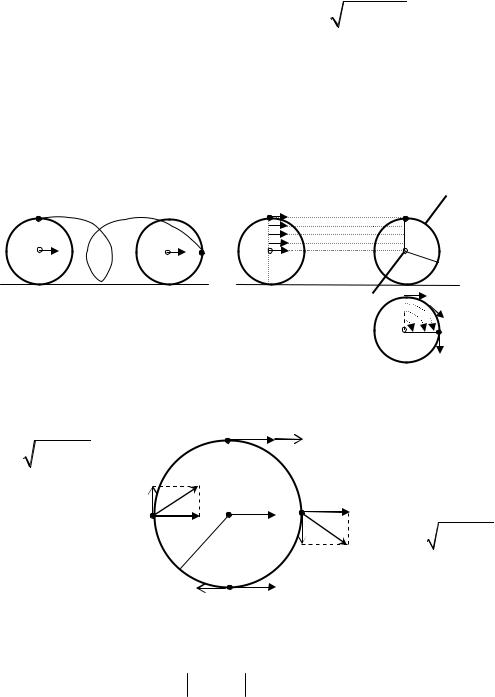
1. Твердое тело начинает вращаться вокруг осиZ с угловой скоростью, проекция которой изменяется со временем, как показано на графике.
Угловое перемещение (в радианах) в промежутке времени от 4 с до 8 с равно..0
Решение
t2
По определению Djz =j2 z - j1z =òwz dt - площадь под кривой wz от t .
t1
Площадь первого треугольника с учетом знака(от 4 с до 6 с) – это поворот на угол (угловое перемещение)
Площадь второго треугольника с учетом знака (от 6 с до 8 с) – поворот на угол
(т. е. в обратном направлении). Следовательно, с 4 с по 8 с тело повернется на угол 0,5 - 0,5 = 0рад.
Примечание. Достаточно было посчитать |
площади треугольников в |
клеточ- |
|||||||
ках, чтобы понять, что ответ 0. |
|
|
|
|
|
|
|||
2. |
|
Диск вращается |
вокруг своей |
оси, зменяя проекцию |
угловой |
скорости |
|||
w |
|
|
|
|
|
|
r |
|
|
z |
(t) так, как показано на рисунке. Вектор угловой скорости w и вектор угло- |
||||||||
|
r |
направлены в |
одну |
сторону |
в |
интервалы времени… |
|||
вого ускорения e |
|||||||||
|
|
|
|
|
от 0 до t1 |
и от |
t2 до t3 |
||
|
|
|
|
|
от 0 до t1 |
и от |
t1 до |
t2 |
|
|
|
|
|
|
от t1 до t2 и от t2 до t3 |
||||
|
|
|
|
|
от 0 до t1 |
и от |
t3 до |
t4 |
|
13
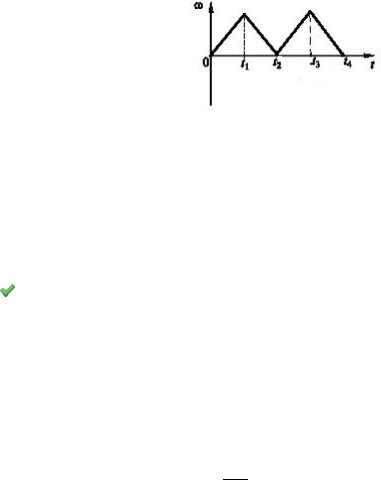
Решение
Вектор угловой скорости=w| и вектор| углового ускорения e направлены в одну сторону при ускоренном вращении, т.е. когда модуль ω растет со временем. Построим зависимость ω ω от t .
Следовательно, w растет на участках от 0 до t1 и от t2 до t3 .
3. Частица из состояния покоя начала двигаться по дуге окружности радиуса R = 2 м с угловой скоростью, модуль которой изменяется с течением времени по закону ω = 2t2. Отношение нормального ускорения к тангенциальному через 2 секунды равно …8
8
4
1
2
Решение
Нормальное ускорение частицы равно
ω
где R – радиус |
кривизны |
траектории.Тангенциальное ускорение определяется |
|||||||||
= |
|
= |
|
|
= 4 |
ω |
, |
||||
выражением |
|
|
|
|
|
(ω ) |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Следовательно, |
отношение |
нормального ускорения к тангенциальному через |
|||||||||
= |
= |
= |
|
|
= |
|
= 4 . |
||||
2 с равно |
|
|
|
|
|
|
= 8 . |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
4. Диск катится равномерно по |
горизонтальной поверхности со скоростью |
||||||||||
без проскальзывания. Вектор скорости точки А, лежащей на ободе диска, |
|||||||||||
ориентирован |
в направлении… |
|
|
|
|
|
|
|
|||
14
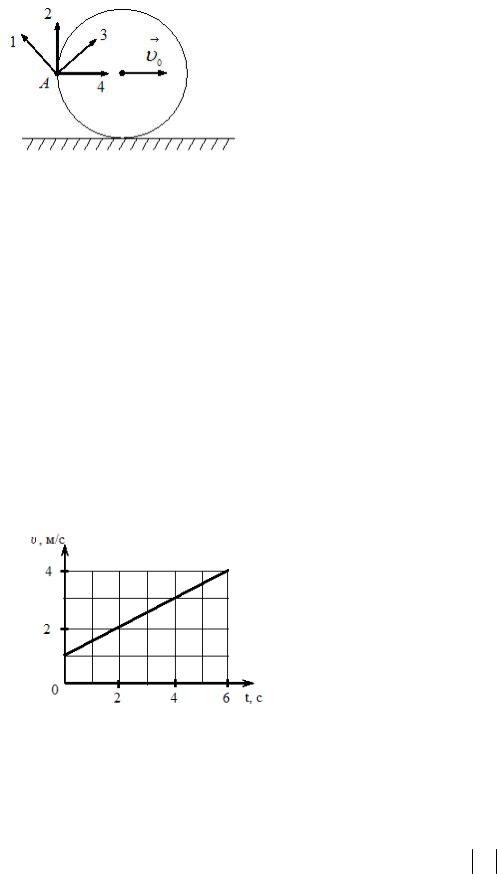
 3 1 2 4
3 1 2 4
Решение
Качение однородного кругового цилиндра (диска) по плоскости является плоским движением, которое можно представить как совокупность двух дви-
жений: поступательного, происходящего со скоростью |
центра масс, и враща- |
||||||
|
|
= |
+ |
|
|
|
направлена по ка- |
тельного вокруг оси, проходящей через этот центр (скорость |
|||||||
сательной к окружности). Тогда |
|
|
вр (см. теоретическую часть). Век- |
||||
тор скорости |
точки А ориентирован |
в направлении |
3. |
|
|
||
Примечание. Отсутствие проскальзывания никакой роли не играет.
5. Твердое тело вращается вокруг неподвижной оси. Скорость точки, находящейся на расстоянии 10 см от оси, изменяется со временем в соответствии с графиком, представленным на рисунке. Угловое ускорение тела(в единицах СИ) равно …
 5 0,5 0,05 50
5 0,5 0,05 50
Решение
Так как модуль скорости растет линейно, то это равноускоренное движение по окружности. Тогда
u(t=) u + a t и a = |
u - u0 |
= |
|
a |
|
> 0. |
|||
|
|
||||||||
|
|||||||||
0 |
t |
t |
t |
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
||
Тангенциальное ускорение связано с угловым уравнением at = eR . Тогда
e = |
|
at |
|
= |
u - u |
0 |
|
= |
4 -1 |
= 5рад/с2 или с-2. |
|
|
|
|
|
|
|||||
|
R |
|
tR |
|
|
|
||||
|
|
|
|
|
|
|
6 ×0,1 |
|||
15

6. Точка М движется по спирали с равномерно убывающей скоростью в направлении, указанном стрелкой. При этом величина полного ускорения точки …
уменьшается
увеличивается не изменяется равна нулю
= |
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Величина |
|
полного |
|
|
ускорения |
определяется |
соотнош |
||||||||||
|
τ |
|
, где τ |
|
и |
– проекция тангенциального и нормального ус- |
||||||||||||
корения соответственно |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
где R – радиус кривизны |
|
τ |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
траектории. Так как по условию скорость убывает рав- |
||||||||||||||||||
|
|
= |
, |
= |
|
, |
|
|
|
|
|
|||||||
Так как по условию скорость |
|
= |
|
= const. |
|
|
|
|
|
|
||||||||
номерно (т. е. линейно с ростом t), то |
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
τ |
|
|
|
|
|
|
|
|
|
|
|
|
(смотри рисунок), то |
|
|
убывает, |
а радиус кривизны траектории R растет |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
уменьшается. Таким образом, полное |
ускорение |
точки |
|
|
|
|
умень- |
|||||||||||
|
τ |
|
|
|||||||||||||||
= |
|
|
|
= |
+ |
|
||||||||||||
шается. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
7. Точка М движется по спирали с постоянной по величине скоростью в- на правлении, указанном стрелкой. При этом величина нормального ускорения…
увеличивается
уменьшается не изменяется равна нулю
Решение
Так как по условию скорость постоянна, а радиус кривизны траектории R растет (смотри рисунок), то величина нормального= ускорения
уменьшается.
16

8. Точка М движется по спирали с постоянным по величине нормальным уско-
рением в направлении, указанном стрелкой. При этом проекция тангенциально-
го ускорения на направление скорости
меньше нуля больше нуля равна нулю
Решение |
|
|
= |
|
= const, |
|||
то |
|
|
|
|||||
Так как нормальное ускорение |
|
|
|
|||||
|
= |
|
|
|
|
|||
Так как со временем(с ростом t) |
const√ |
|
. |
|||||
|
||||||||
|
|
. |
|
радиус R (смотри рисунок) уменьшается, то |
||||
уменьшается |
и |
Тогда проекция тангенциального ускорения на направление |
||||||
скорости |
|
|
τ = |
< 0. |
||||
|
|
|
|
|
|
|
||
9. Материальная точка М движется по окружности со скоростью . График за- |
||||||||
висимости τ |
от времени (τ – единичный вектор положительного направления, |
|||||||
τ |
– проекция |
на это направление) показан на рисунке. При |
этом для нор- |
|||||||||
|
|
|
|
|
|
|
|
|
|
|||
мального |
|
|
и тангенциального τ ускорений выполняются условия |
|
||||||||
|
|
|
= 0, |
τ > 0 |
|
|
|
|
|
|||
|
|
|
> 0, |
τ = 0 |
|
|
|
|
|
|||
|
|
|
= 0, |
τ = 0 |
|
|
|
|
|
|||
Решение |
> 0, |
τ > 0 |
|
|
= |
, |
|
− |
|
|||
|
|
|
||||||||||
|
|
|
||||||||||
|
|
|
|
|
|
|
||||||
Так как |
|
τ |
|
и линейно зависит от времени, то |
где |
положи- |
||||||
тельная |
константа. |
|
|
|||||||||
|
|
= |
|
|
|
|
|
|||||
17
Тогда |
|
|
|
= |
= |
> 0, |
τ = |
= |
> 0. |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Следовательно, |
> 0, |
|
τ > 0. |
|
|
|
|
|
|
|
|
|
|||||||||||
10. Материальная точка М движется по окружности со скоростью |
. График |
||||||||||||||||||||||
зависимости τ |
от времени (τ– единичный вектор положительного |
направле- |
|||||||||||||||||||||
ния, |
τ – |
проекция |
на |
это направление) показан на рисунке. При этом для |
|||||||||||||||||||
нормального |
и тангенциального |
τ |
ускорений выполняются условия |
||||||||||||||||||||
|
|
|
– увеличивается, |
|
τ – постоянно |
|
|
|
|
|
|
|
|||||||||||
|
|
|
– постоянно, |
τ – постоянно |
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
– увеличивается, |
|
τ – величивается |
|
|
|
|
|
|
|
|||||||||||
|
|
|
– постоянно, |
τ – увеличивается |
|
|
|
|
|
|
|
||||||||||||
тельная |
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
, |
|
|
|
|||||
Решение |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Так |
как |
|
τ |
|
и линейно |
зависит |
от |
времени, то |
= . |
|
где |
|
положи- |
||||||||||
|
|
константа, и |
= |
|
|
= |
|
|
, |
τ = |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Следовательно, |
– увеличивается, |
τ – постоянно. |
|
|
|
|
|
|
|
||||||||||||||
11. Тело движется с постоянной по величине скоростью по траектории, изображенной на рисунке. Для величин полного ускорения тела в точкахА и В справедливо соотношение …
Решение |
|
|
|
|
|
|
|
Величина полного ускорения |
|
τ |
|
, где τ и |
– проекции |
||
тангенциального и нормального |
ускорения соответственно. По определению |
||||||
|
= |
|
+ |
|
|
|
|
|
|
18 |
|
|
|
|
|

τ = |
τ |
|
|
|
|
|
|
= const. |
|
= |
= |
|
|
||||
= 0, |
|
|
|
|||||
где R – радиус кривизны |
траектории. По условию скорость постоянна. Тогда |
|||||||
|
= |
, |
= |
|
|
, |
|
|
Так как радиус кривизны траектории в точке А (смотри рисунок) меньше, чем в точке В, то, следовательно, полное ускорение в точке А больше, чем в точке В.
12. Камень бросили под углом к горизонту со скоростьюv . Его траектория в
однородном поле тяжести изображена на рисунке. Сопротивления воздуха нет.
Нормальное ускорение на участке А-В-С …
уменьшается
увеличивается не изменяется
Решение |
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r |
|
|
a |
|
gt = 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
gt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
r |
r |
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a0 |
r |
gn |
g |
= gn |
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
r |
g |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
gt |
a0 gn |
|
|
|
|
= на нормальную и тангециальную со- |
||||||||||||
|
|
r |
|
|
|
|
|||||||||||||
|
|
g |
|
|
|
|
|||||||||||||
Разложим вектор ускорения |
|||||||||||||||||||
ставляющие |
|
= |
|
|
=α |
|
|||||||||||||
Так как угол α |
|
|
|
cos |
α, |
=α |
|
= |
sin . |
α |
τ cos0τ |
= 1 |
|
||||||
участке А-В-С, то |
|
|
|
|
|
|
cos |
|
|
|
cos |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
α |
|
|
|
|
|
||
|
уменьшается от |
до 0, а |
|
растет от |
|
|
|
до |
|
|
на |
||||||||
|
|
= |
|
|
увеличивается на подьеме до |
, а |
|
= |
умень- |
||||||||||
шается до 0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
13. Камень бросили под углом к горизонту со скоростью |
|
. Его траектория в |
|||||||||||||||||
однородном поле тяжести изображена на рисунке. |
Сопротивления воздуха нет. |
||||||||||||||||||
|
|
|
v |
|
|
|
|
|
|||||||||||
Модуль полного ускорения камня …
19
