
- •Электромагнетизм Тестовые задания
- •Предисловие
- •1. Электрическое поле (эп)
- •1.1. Расчетные формулы по теме «эп»
- •1.2. Тестовые задания по теме «эп»
- •2. Электроемкость и конденсаторы (эк)
- •2.1. Расчетные формулы по теме «эк»
- •2.2. Тестовые задания по теме «эк»
- •3. Законы постоянного тока (зпт)
- •3.1. Расчетные формулы по теме «зпт»
- •3.2. Тестовые задания по теме зпт
- •4.Магнитное поле тока (мпт)
- •4.1. Определения основных понятий мпт
- •4.2.Основные формулы раздела «мпт»
- •4.3. Тестовые задания по теме «мпт»
- •4.4. Задачи на тему «мпт»
- •5. Сила Лоренца (сл)
- •5.1. Расчетные формулы
- •5.2. Тестовые задания по теме «сл»
- •6. Электромагнетизм (эм)
- •6.1. Электромагнитная индукция и самоиндукция
- •6.2. Расчетные формулы по теме «эм»
- •6.3. Тестовые задачи по теме «эм»
- •7. Электромагнитные колебания (эмк)
- •7.1. Собственные незатухающие электромагнитные колебания
- •7.2. Собственные затухающие эмк
- •7.3. Расчетные формулы по теме «эмк»
- •7.4. Расчетные формулы в заданиии «переменный ток»
- •7.5. Тестовые задания по теме эмк
- •8.Библиографический список
- •Электромагнетизм Тестовые задания
- •620034, Екатеринбург, ул. Колмогорова, 66 Приложение
7.3. Расчетные формулы по теме «эмк»
Свободные ЭМК (0 – максимальное значение).
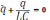
 – дифференциальное уравнение, описывающее
свободные гармонические колебания
заряда в колебательном контуре.
– дифференциальное уравнение, описывающее
свободные гармонические колебания
заряда в колебательном контуре.
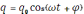
 – закон изменения заряда q
(силы тока
– закон изменения заряда q
(силы тока 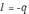
 ,
ЭДС самоиндукции
,
ЭДС самоиндукции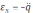
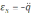 )
в зависимости от времени электромагнитных
гармонических колебаний .
)
в зависимости от времени электромагнитных
гармонических колебаний .
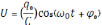 –
закон изменения напряжения на
конденсаторе.
–
закон изменения напряжения на
конденсаторе.
 – закон изменения силы тока в контуре.
– закон изменения силы тока в контуре.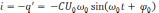

 – закон изменения ЭДС самоиндукции в
контуре.
– закон изменения ЭДС самоиндукции в
контуре.
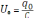 –
амплитуда напряжения.
–
амплитуда напряжения.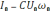
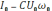 –
амплитуда силы тока.
–
амплитуда силы тока. 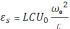
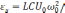
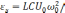 C –
изменение ЭДС самоиндукции.
C –
изменение ЭДС самоиндукции.

 – собственная частота контура, q0
– амплитуда колебаний заряда.
– собственная частота контура, q0
– амплитуда колебаний заряда.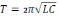
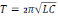 –
формула Томсона.
–
формула Томсона.



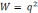
 /
2C
+ Li2
/
2 – полная энергия электромагнитного
поля колебательного контура.
/
2C
+ Li2
/
2 – полная энергия электромагнитного
поля колебательного контура.
Затухающие ЭМК
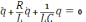
 – уравнение затухающих колебаний.
– уравнение затухающих колебаний.
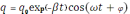 – закон изменения заряда.
– закон изменения заряда.
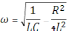 – циклическая частота затухающих
колебаний.
– циклическая частота затухающих
колебаний.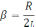
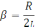 –
коэффициент затухания.
–
коэффициент затухания.
 = ln(At
/ At
+T)
=
= ln(At
/ At
+T)
= 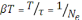
 –
логарифмический декремент затухания,Ne
– число колебаний за время релаксации.
–
логарифмический декремент затухания,Ne
– число колебаний за время релаксации.
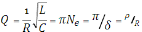 – добротность контура.
– добротность контура.
7.4. Расчетные формулы в заданиии «переменный ток»
(приложено
напряжение 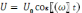


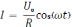 – переменный ток текущий через резистор
сопротивлением R.
– переменный ток текущий через резистор
сопротивлением R.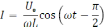
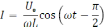 −
переменный ток, текущий через катушку
индуктивностью L.
−
переменный ток, текущий через катушку
индуктивностью L.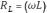
 –
индуктивное сопротивление.
–
индуктивное сопротивление.
 –
переменный ток, текущий через конденсатор
емкостью С.
–
переменный ток, текущий через конденсатор
емкостью С.
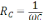 –
емкостное сопротивление.
–
емкостное сопротивление.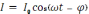
 ;
;

 – переменный ток, текущий в цепи
(последовательное RLC,
– переменный ток, текущий в цепи
(последовательное RLC,
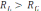
 ).
).
 − полное сопротивление цепи RLC
переменному току(RL
− полное сопротивление цепи RLC
переменному току(RL >RC).
>RC).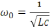
 –
резонансная циклическая частота.
–
резонансная циклическая частота.Действующее (эффективное) значение тока
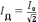
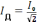 и
напряжения
и
напряжения 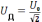
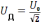 .
.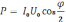
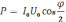 –
средняя мощность цепи переменного
тока.
–
средняя мощность цепи переменного
тока.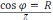


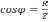
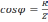 –
коэффициент мощности.
–
коэффициент мощности.
7.5. Тестовые задания по теме эмк
ЭМК
1. В
LC
контуре конденсатор зарядили и отключили.
Свободные ЭМК в LC
контуре. Находятся параметры в
конденсаторе: C
– электрическая емкость, q
–
заряд, Wоэ−
энергия электрического поля, E0
– напряженность электрического поля,
0
– объемная плотность энергии. В катушке:
W0м
– энергия магнитного поля, L
– индуктивность катушки, 0
– потокосцепление, В0
–
индукция магнитного поля, Ф – магнитный
поток, ом
–
плотность энергии магнитного поля, so
–
ЭДС самоиндукции, RL
– индуктивное сопротивление, Rc
– емкостное сопротивление. Индекс 0
обозначает амплитудное значение
колеблющихся величин ( ).
Сначала конденсатор был заряжен, а затем
отключен от источника. Это первое (1)
состояние контура. Далее в конденсатор
ввели диэлектрик (2)
(
).
Сначала конденсатор был заряжен, а затем
отключен от источника. Это первое (1)
состояние контура. Далее в конденсатор
ввели диэлектрик (2)
(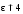 ).
Параметры конденсатораd,
S
и катушки ,
N,
S
не
меняются. Во сколько раз изменятся
максимальные значения параметров
контура?
).
Параметры конденсатораd,
S
и катушки ,
N,
S
не
меняются. Во сколько раз изменятся
максимальные значения параметров
контура?
Решение:
емкость
 ,
заряд не меняется (q
=),
энергия электрического поля в конденсаторе
,
заряд не меняется (q
=),
энергия электрического поля в конденсаторе
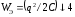 ,
напряженность электрического поля
,
напряженность электрического поля ,
объемная плотность энергии электрического
поля
,
объемная плотность энергии электрического
поля
 ,
энергия магнитного поляWОЭ
= WОМ4,
индуктивность
,
энергия магнитного поляWОЭ
= WОМ4,
индуктивность
 не меняется. Из соотношенияq2/C
~ Li2
получим I
↓
2, В
↓ 2,
магнитный поток
не меняется. Из соотношенияq2/C
~ Li2
получим I
↓
2, В
↓ 2,
магнитный поток
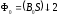 ,
потокосцепление
,
потокосцепление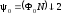 .
Объемная плотность энергии магнитного
поляОМ
=
(B2/2μ0μ)4,
ЭДС самоиндукции
.
Объемная плотность энергии магнитного
поляОМ
=
(B2/2μ0μ)4,
ЭДС самоиндукции
 ,
циклическая частота
,
циклическая частота ,
индуктивное сопротивление
,
индуктивное сопротивление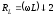 ,
период
,
период ,
частота
= (1/T)
2, емкостное сопротивление
,
частота
= (1/T)
2, емкостное сопротивление
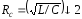 ,
сила взаимодействия между пластинами
,
сила взаимодействия между пластинами .
.
ЭМК
2. Контур
 в цепи переменного тока.
Как изменятся параметры переменного
тока, если частоту колебаний переменного
тока увеличить (ω
в цепи переменного тока.
Как изменятся параметры переменного
тока, если частоту колебаний переменного
тока увеличить (ω ):
φ – сдвиг фазы между током и напряжением,
):
φ – сдвиг фазы между током и напряжением,
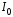 – амплитуда силы тока,Iд
–
действующее значение силы тока, Uд
– действующее значение напряжения,
Q
– реактивная мощность. Параметры
– амплитуда силы тока,Iд
–
действующее значение силы тока, Uд
– действующее значение напряжения,
Q
– реактивная мощность. Параметры
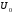 ,L,
,L,
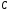 ,
,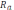
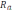 не меняются, причем .
не меняются, причем .
Решение.
Сдвиг фазы между током и напряжением
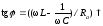 импеданс
сопротивлений
импеданс
сопротивлений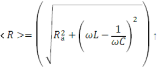
 ,
максимальное значение силы тока
,
максимальное значение силы тока ,
действующее значение силы тока
,
действующее значение силы тока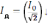
 ,
действующее значение напряжения
,
действующее значение напряжения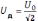
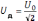 не меняется, реактивная мощность
не меняется, реактивная мощность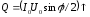 .
Активная мощность
.
Активная мощность
ЭМК
3. Свободные
электромагнитные колебания в
 контуре.
Напряжение
на конденсаторе изменяется по закону
синуса
(
контуре.
Напряжение
на конденсаторе изменяется по закону
синуса
( ).
При
).
При
 →
→
 ;
; .
Параметры конденсатораS,
d,
ε
и
катушки N,
S,
𝓁,
μ не меняются. Находятся параметры
конденсатора: q,
E,
.
Параметры конденсатораS,
d,
ε
и
катушки N,
S,
𝓁,
μ не меняются. Находятся параметры
конденсатора: q,
E,

 ,
,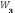
 ,Rc,
,Rc,
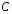 ,
катушки:Wм,
,
катушки:Wм,
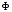 ,B,
H,
ψ,
,B,
H,
ψ,
 ,
,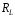 ,
,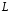 ,
далееT,
ω. С учетом сдвига фазы колебаний
определите параметры контура, которые
в момент времени t
= T/4
принимают
положительные
максимальное
,
далееT,
ω. С учетом сдвига фазы колебаний
определите параметры контура, которые
в момент времени t
= T/4
принимают
положительные
максимальное
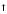 ,
равное нулю
,
равное нулю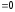 ,
отрицательное минимальное
,
отрицательное минимальное значения. Значение величины не меняется
(=).
значения. Значение величины не меняется
(=).
Решение.
Напряжение
 ,
значит,
,
значит,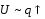 ,
,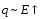 ,
,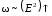 ,
,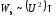 ,
, ,
,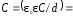 .
В этот момент времени сила тока
.
В этот момент времени сила тока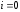 ,
значит
Wм=0,
,
значит
Wм=0,
 ,
,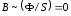 ,
,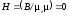 ,
,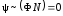 ,
,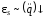 ,
, ,
,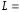 ,
,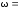 ,T
= .
,T
= .
ЭМК
4. В контуре RLC
конденсатор зарядили, затем его отключили
от источника, и далее ввели в него
диэлектрик
.
В ЭМК заряд не меняется (q=)
с увеличением емкости
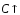 (приd=)
напряженность электрического поля в
конденсаторе
(приd=)
напряженность электрического поля в
конденсаторе
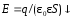 ,
напряжение
,
напряжение ,
энергия электрического поля
,
энергия электрического поля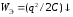 ,
плотность энергии
,
плотность энергии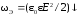 ,
период
,
период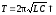 ,
циклическая частота колебаний
,
циклическая частота колебаний ,
емкостное сопротивление
,
емкостное сопротивление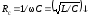 ,
коэффициент затухания
,
коэффициент затухания .
.
ЭМК
5. Свободные
ЭМК в LC
контуре.
Сначала конденсатор
был заряжен и отключен от источника
( ).
R
).
R
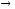 0. Это первое (1) состояниеLC
контура. Затем изменили (2) параметры
электрического (магнитного) поля в
LC
контуре. Во сколько раз (С2/С1)
изменятся максимальные (0) параметры в
LC
контуре: 1) С
– электрическая емкость, 2) q0
– электрический заряд, 3) W0
– энергия электрического поля, 4)
0. Это первое (1) состояниеLC
контура. Затем изменили (2) параметры
электрического (магнитного) поля в
LC
контуре. Во сколько раз (С2/С1)
изменятся максимальные (0) параметры в
LC
контуре: 1) С
– электрическая емкость, 2) q0
– электрический заряд, 3) W0
– энергия электрического поля, 4)
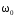 – плотность энергии магнитного поля,
5)В0
– магнитная индукция. Далее: 1)
– плотность энергии магнитного поля,
5)В0
– магнитная индукция. Далее: 1)
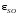 – ЭДС самоиндукции, 2)RL
– индуктивное сопротивление, 3)
– ЭДС самоиндукции, 2)RL
– индуктивное сопротивление, 3)
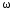 – циклическая частота колебаний, 4)T
– период колебаний, 5) L
–
индуктивность катушки, если во втором
состоянии напряженность электрического
поля
– циклическая частота колебаний, 4)T
– период колебаний, 5) L
–
индуктивность катушки, если во втором
состоянии напряженность электрического
поля 
 ↓ 4. Параметры конденсатораd,
S
и катушки
↓ 4. Параметры конденсатораd,
S
и катушки
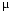 ,N,
S,
𝓁не
менять.
,N,
S,
𝓁не
менять.
Задаваемые
параметры: q,
E,
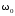 ,
U,
ε,
d,
S,
,
U,
ε,
d,
S,
 ,
N.
,
N.
ЭМК
6. Свободные
ЭМК в LC
контуре.
Напряжение на конденсаторе изменяется
по закону синуса (косинуса). При t
= 0
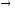
 0
=
0; R
0
=
0; R 0.
Находятся: 1) q
–
электрический заряд, 2) E
– напряженность электрического поля,
3) Rc
– емкостное сопротивление, 4)
0.
Находятся: 1) q
–
электрический заряд, 2) E
– напряженность электрического поля,
3) Rc
– емкостное сопротивление, 4) 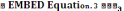
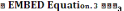 –
плотность энергии электрического поля,
5)
W
– энергия электрического поля. 1) В
– магнитная индукция, 2)
Ф
– магнитный поток, 3) εS
– ЭДС самоиндукции, 4)
–
плотность энергии электрического поля,
5)
W
– энергия электрического поля. 1) В
– магнитная индукция, 2)
Ф
– магнитный поток, 3) εS
– ЭДС самоиндукции, 4) 
 –
плотность энергии магнитного поля, 5)RL
– индуктивное сопротивление. С учетом
сдвига фазы колебаний укажите параметры
LC
контура, которые в момент времени t
принимают положительное максимальное
(+
–
плотность энергии магнитного поля, 5)RL
– индуктивное сопротивление. С учетом
сдвига фазы колебаний укажите параметры
LC
контура, которые в момент времени t
принимают положительное максимальное
(+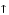 ),
равное = 0, отрицательное максимальное
(–
),
равное = 0, отрицательное максимальное
(–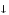 )
значения. Значение параметра не меняется
(=). Принятьt
= T/4.
)
значения. Значение параметра не меняется
(=). Принятьt
= T/4.
Задаваемые параметры: T/4, T/2, 3T/4, T, 3T/2, 5T/4.
+

 ЭМК
7. К нижним концам двух пружин с
коэффициентом упругости
ЭМК
7. К нижним концам двух пружин с
коэффициентом упругости 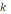
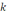 у каждой прикреплены концы расположенного
горизонтально металлического стержня
длиной
у каждой прикреплены концы расположенного
горизонтально металлического стержня
длиной
 и массой
и массой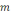
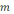 .
Верхние концы пружин соединены проволокой
через конденсатор емкостью
.
Верхние концы пружин соединены проволокой
через конденсатор емкостью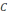
 .
Стержень колеблется в вертикальной
плоскости с амплитудой
.
Стержень колеблется в вертикальной
плоскости с амплитудой
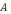 .
Весь стержень постоянно находится в
однородном магнитном поле с индукцией
.
Весь стержень постоянно находится в
однородном магнитном поле с индукцией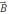
 ,
вектор которой горизонтален и
перпендикулярен стержню. Массой пружин
пренебречь. Индекс
,
вектор которой горизонтален и
перпендикулярен стержню. Массой пружин
пренебречь. Индекс
 – максимальное амплитудное значение
величины. Пружины проводящие. Сопротивление
всей цепи
– максимальное амплитудное значение
величины. Пружины проводящие. Сопротивление
всей цепи
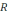 .
Индуктивностью цепи пренебречь.
Обозначения: 1)
.
Индуктивностью цепи пренебречь.
Обозначения: 1)
 – циклическая частота колебаний, 2)
– циклическая частота колебаний, 2)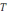
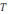 – период, 3)
– период, 3)
 – частота, 4)
– частота, 4)
 – максимальная (0) скорость, 5)
– максимальная (0) скорость, 5)
 – ускорение, 6)
– ускорение, 6)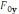
 – сила упругости, 7)
– сила упругости, 7)
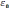 – индукционная ЭДС, 8)
– индукционная ЭДС, 8)
 – заряд в конденсаторе, 9)
– заряд в конденсаторе, 9)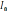
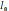 – сила тока, 10)
– сила тока, 10)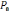
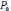 – мощность тока, 11)
– мощность тока, 11)
 – сила Ампера, 12) – энергия электрического
поля, 13)
– сила Ампера, 12) – энергия электрического
поля, 13)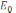
 –
напряженность электрического поля, 15)
–
напряженность электрического поля, 15)
 – ЭДС самоиндукции. Во сколько раз
изменятся значения параметров, если в
задаче изменится один параметр, а
остальные не меняются?
– ЭДС самоиндукции. Во сколько раз
изменятся значения параметров, если в
задаче изменится один параметр, а
остальные не меняются?
Дано: c, k, m, B, 𝓁, R, d, A0.
Найти:
1) ω, 2) 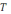
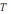 ,
3)
,
3)
 ,
4)
,
4) 
 ,
5)
,
5) 
 ,
6)
,
6) 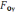
 ,
7)
,
7) 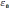
 ,
8)
,
8) 
 ,
9)
,
9) 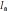
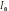 ,
10)
,
10) 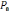
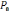 ,
,
11)
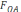
 ,
12) ,
13)
,
12) ,
13) 
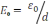 , 14)
, 14)
 ,
15)
,
15) 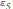
 .
.
Расчетные формулы:
1) 2k = mω2,
2)
T

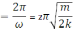 ,
,
3)
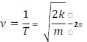


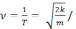
 2π,
2π,
4)

 ,
,
5)
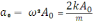
 ,
,
6)

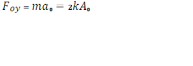 ,
,
7)
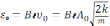
 ,
,
8)
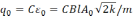 ,
,
9)
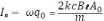
 ,
10)
,
10) 
 ,
,
11)
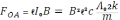
 ,
,
12) Wэо = Cε02 / 2 = (CB2l2A022k) / 2m,
13)
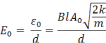 ,
,
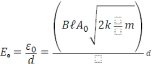
14) ω0 = Wэо / V = (CB2l2A02 2k) / 2mV ,
15)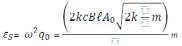


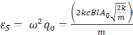
 .
.
