
- •Электромагнетизм Тестовые задания
- •Предисловие
- •1. Электрическое поле (эп)
- •1.1. Расчетные формулы по теме «эп»
- •1.2. Тестовые задания по теме «эп»
- •2. Электроемкость и конденсаторы (эк)
- •2.1. Расчетные формулы по теме «эк»
- •2.2. Тестовые задания по теме «эк»
- •3. Законы постоянного тока (зпт)
- •3.1. Расчетные формулы по теме «зпт»
- •3.2. Тестовые задания по теме зпт
- •4.Магнитное поле тока (мпт)
- •4.1. Определения основных понятий мпт
- •4.2.Основные формулы раздела «мпт»
- •4.3. Тестовые задания по теме «мпт»
- •4.4. Задачи на тему «мпт»
- •5. Сила Лоренца (сл)
- •5.1. Расчетные формулы
- •5.2. Тестовые задания по теме «сл»
- •6. Электромагнетизм (эм)
- •6.1. Электромагнитная индукция и самоиндукция
- •6.2. Расчетные формулы по теме «эм»
- •6.3. Тестовые задачи по теме «эм»
- •7. Электромагнитные колебания (эмк)
- •7.1. Собственные незатухающие электромагнитные колебания
- •7.2. Собственные затухающие эмк
- •7.3. Расчетные формулы по теме «эмк»
- •7.4. Расчетные формулы в заданиии «переменный ток»
- •7.5. Тестовые задания по теме эмк
- •8.Библиографический список
- •Электромагнетизм Тестовые задания
- •620034, Екатеринбург, ул. Колмогорова, 66 Приложение
7. Электромагнитные колебания (эмк)
7.1. Собственные незатухающие электромагнитные колебания
1.
Контур LC.
Электромагнитный колебательный контур
(ЭМК) состоит из конденсатора емкостью
С
= ε0εS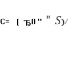 / d
с емкостным сопротивлением
/ d
с емкостным сопротивлением 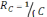 RC
= 1/ωC
и катушки индуктивностью L
= μ0μN2S/l
RC
= 1/ωC
и катушки индуктивностью L
= μ0μN2S/l
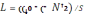 ,
индуктивным сопротивлениемRL
= ωL,
где
– относительная диэлектрическая
проницаемость среды,
– относительная магнитная проницаемость
среды,
–
циклическая частота,
,
индуктивным сопротивлениемRL
= ωL,
где
– относительная диэлектрическая
проницаемость среды,
– относительная магнитная проницаемость
среды,
–
циклическая частота,
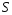 – площадь,d
– расстояние между пластинами
конденсатора, N
–
число витков в катушке. Максимальная
энергия электрического (э) поля в
конденсаторе, максимальная энергия
магнитного (м) поля в катушке. В любой
момент времени суммарная энергия. При
удельном сопротивлении
→
– площадь,d
– расстояние между пластинами
конденсатора, N
–
число витков в катушке. Максимальная
энергия электрического (э) поля в
конденсаторе, максимальная энергия
магнитного (м) поля в катушке. В любой
момент времени суммарная энергия. При
удельном сопротивлении
→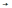 0 убыль энергии ΔW
→
0 убыль энергии ΔW
→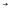 0
0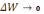 ,
отсюда
,
отсюда
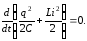
Учитывая,
что сила тока i
= –q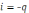 ,
а производная (i)′
,
а производная (i)′
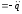 ,
запишем дифференциальное уравнение
,
запишем дифференциальное уравнение
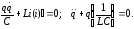
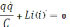
Решением дифференциального уравнения является функция
q = q0cos(ω0t + φ0),
где циклическая частота 0 = 2/Т0; 1/LC = 02.
В
ЭМК изменяются по гармоническому закону:
в конденсаторе – заряд q,
напряжение U,
напряженность электрического поля E,
плотность энергии электрического поля
ω э,
энергия электрического поля Wэ,
поверхностная плотность заряда ;
в катушке
э,
энергия электрического поля Wэ,
поверхностная плотность заряда ;
в катушке – магнитный поток Ф, индукция магнитного
поляB,
напряженность магнитного поля H,
сила тока i,
плотность энергии магнитного поля м,
энергия магнитного поля Wм,
ЭДС самоиндукции εs.
– магнитный поток Ф, индукция магнитного
поляB,
напряженность магнитного поля H,
сила тока i,
плотность энергии магнитного поля м,
энергия магнитного поля Wм,
ЭДС самоиндукции εs.
Ниже приведены соответствующие формулы:
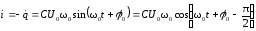 ,
,
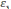
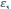
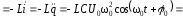
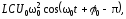
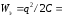
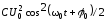 ,
,
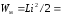
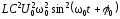 /
2.
/
2.
При
условии
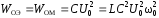 ,получим
,получим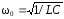 .
.
В
ЭМК заряд q
опережает силу тока i
по фазе на π/2, а ЭДС самоиндукции εs
–
на π, сила тока i
опережает ЭДС самоиндукции
εs
 по фазе на π/2.
по фазе на π/2.
2. Контуры C; L; RLC в цепи переменного напряжения.
а)
На емкость
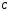 подано переменное напряжение
подано переменное напряжение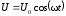 .
.
При
t0
=
0
 0
=
0;
R
= 0,
L
= 0.
В цепи сила тока
0
=
0;
R
= 0,
L
= 0.
В цепи сила тока
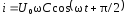 опережает
напряжение по фазе на
опережает
напряжение по фазе на
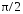 .
.
б)
На индуктивность
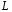 подано напряжение
подано напряжение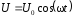 .
.
При
t0
=
0

 0
=
0;
R
= 0,
C
= 0.
В цепи сила тока
0
=
0;
R
= 0,
C
= 0.
В цепи сила тока
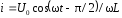 отстает от напряжения по фазе на
отстает от напряжения по фазе на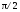 .
.
в)
На контур
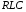 подано напряжение
подано напряжение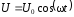 .
При условии
.
При условии сила тока опережает напряжение по фазе
сила тока опережает напряжение по фазе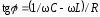 ,
а общее сопротивление цепи (импеданс)
,
а общее сопротивление цепи (импеданс)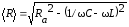 .
.
Закон
Ома
 .
.
Резонанс
напряжения. При
условии
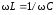 сдвиг фазы
сдвиг фазы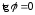 .
Ток и напряжение совпадают по фазе.
Сила тока
.
Ток и напряжение совпадают по фазе.
Сила тока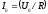 .
.
Активная
мощность
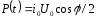 ,
реактивная мощность
,
реактивная мощность
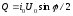 действующее значение напряжения
UД=
действующее значение напряжения
UД=
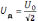 U0
/
U0
/
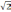 ,
действующее значение силы тока
,
действующее значение силы тока
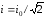 ,
определяемое по тепловому эффекту.
,
определяемое по тепловому эффекту.
7.2. Собственные затухающие эмк
При удельном сопротивлении ρ≠ 0 убыль энергии в контуре RLC равна джоулевой теплоте:

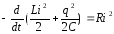 .
.
При
известном условии 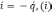
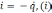 = -
= - 
 запишем дифференциальное уравнение:
запишем дифференциальное уравнение:
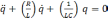
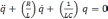 ,
где R/L
=
2β, 1/LC
=
,
где R/L
=
2β, 1/LC
=
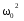 .
Решением дифференциального уравнения
.
Решением дифференциального уравнения
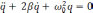 является функция
является функция
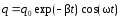 .
.
Затухающие
колебания характеризуются коэффициентом
затухания
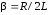 ,
циклической
частотой
,
циклической
частотой
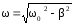 ,
логарифмическим декрементом затухания
,
логарифмическим декрементом затухания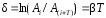 ,
добротностью
,
добротностью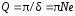 ,
временем релаксации
,
временем релаксации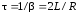 ,
в течение которого амплитуда колебаний
уменьшится вe
раз
(A1/Ai=
e).
Волновое сопротивление
~
,
в течение которого амплитуда колебаний
уменьшится вe
раз
(A1/Ai=
e).
Волновое сопротивление
~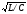 .
При значениях
<
Ra
добротность
контура Q
.
При значениях
<
Ra
добротность
контура Q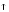 ,
число колебаний за время релаксации
Ne
,
число колебаний за время релаксации
Ne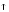 и
наоборот при
>Ra
, следует Q
и
наоборот при
>Ra
, следует Q ,
число колебаний за время релаксации
Ne
↓,
τ↓.
,
число колебаний за время релаксации
Ne
↓,
τ↓.
