
- •Электромагнетизм Тестовые задания
- •Предисловие
- •1. Электрическое поле (эп)
- •1.1. Расчетные формулы по теме «эп»
- •1.2. Тестовые задания по теме «эп»
- •2. Электроемкость и конденсаторы (эк)
- •2.1. Расчетные формулы по теме «эк»
- •2.2. Тестовые задания по теме «эк»
- •3. Законы постоянного тока (зпт)
- •3.1. Расчетные формулы по теме «зпт»
- •3.2. Тестовые задания по теме зпт
- •4.Магнитное поле тока (мпт)
- •4.1. Определения основных понятий мпт
- •4.2.Основные формулы раздела «мпт»
- •4.3. Тестовые задания по теме «мпт»
- •4.4. Задачи на тему «мпт»
- •5. Сила Лоренца (сл)
- •5.1. Расчетные формулы
- •5.2. Тестовые задания по теме «сл»
- •6. Электромагнетизм (эм)
- •6.1. Электромагнитная индукция и самоиндукция
- •6.2. Расчетные формулы по теме «эм»
- •6.3. Тестовые задачи по теме «эм»
- •7. Электромагнитные колебания (эмк)
- •7.1. Собственные незатухающие электромагнитные колебания
- •7.2. Собственные затухающие эмк
- •7.3. Расчетные формулы по теме «эмк»
- •7.4. Расчетные формулы в заданиии «переменный ток»
- •7.5. Тестовые задания по теме эмк
- •8.Библиографический список
- •Электромагнетизм Тестовые задания
- •620034, Екатеринбург, ул. Колмогорова, 66 Приложение
6. Электромагнетизм (эм)
6.1. Электромагнитная индукция и самоиндукция
Возникновение
электродвижущей силы εинд
 в
замкнутом контуре при изменении внешнего
магнитного потока Ф, пронизывающего
контур, называется явлениемэлектромагнитной
индукции
(закон Фарадея): εинд
в
замкнутом контуре при изменении внешнего
магнитного потока Ф, пронизывающего
контур, называется явлениемэлектромагнитной
индукции
(закон Фарадея): εинд

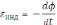 .
.
По
закону Ома индукционный ток

 ,
здесьR
– сопротивление контура. Знак «минус»
в законе Фарадея является следствием
закона сохранения энергии и соответствует
правилу Ленца, согласно которому
индукционный ток направлен так, что его
индукционный поток противодействует
изменениям основного внешнего магнитного
потока Ф.
,
здесьR
– сопротивление контура. Знак «минус»
в законе Фарадея является следствием
закона сохранения энергии и соответствует
правилу Ленца, согласно которому
индукционный ток направлен так, что его
индукционный поток противодействует
изменениям основного внешнего магнитного
потока Ф.
Пусть
к источнику ЭДС ε подключены два параллельных проводника,
по которым скользит перемычка во внешнем
магнитном поле Ф.
Согласно
закону сохранения энергии, полная работа
тока (Iεdt)
за время dt
равна джоулевой теплоте (I2Rdt)
и работе (IdФ)
по перемещению проводника с током в
магнитном поле: Iεdt
= I2Rdt
+ IdФ
подключены два параллельных проводника,
по которым скользит перемычка во внешнем
магнитном поле Ф.
Согласно
закону сохранения энергии, полная работа
тока (Iεdt)
за время dt
равна джоулевой теплоте (I2Rdt)
и работе (IdФ)
по перемещению проводника с током в
магнитном поле: Iεdt
= I2Rdt
+ IdФ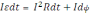 .
Отсюда
.
Отсюда
 .
.
Величина
индукционного магнитного потока Финд,
создаваемого самим текущим по контуру
током I,
равна Финд
= LI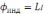 ,
где L
–
индуктивность контура (коэффициент
самоиндукции). По закону полного тока,
циркуляция магнитной индукции Bl
,
где L
–
индуктивность контура (коэффициент
самоиндукции). По закону полного тока,
циркуляция магнитной индукции Bl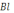 (внутри соленоида) равна произведению
μ0μ
(внутри соленоида) равна произведению
μ0μ на алгебраическую сумму токов,
пронизывающему этот контур:
Bl
= μ0μNI.
Значит,
модуль вектора магнитной индукции
внутри соленоида B
= μ0μnI,
где n
– число витков на единицу длины.
Индуктивность соленоида
на алгебраическую сумму токов,
пронизывающему этот контур:
Bl
= μ0μNI.
Значит,
модуль вектора магнитной индукции
внутри соленоида B
= μ0μnI,
где n
– число витков на единицу длины.
Индуктивность соленоида

 ,
гдеS
–
площадь, l
–
длина соленоида.
,
гдеS
–
площадь, l
–
длина соленоида.
Индукционная ЭДС, которая возникает в контуре с индуктивностью L, по закону Фарадея. Если индуктивность цепи L остается неизменной то, индуциионная ЭДС εинд всегда возникает в контуре при изменении тока I в самом этом контуре. Это явление называется самоиндукцией. Токи, возникающие вследствие самоиндукции, направлены, согласно правилу Ленца, так, чтобы противодействовать изменениям первоначального тока в контуре. Это приводит к тому, что увеличение тока при замыкании и уменьшение при размыкании цепи контура происходит не мгновенно, а постепенно.
Пусть
по цепи RLε (с ЭДС ε, индуктивностьюL
(с ЭДС ε, индуктивностьюL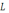 и сопротивлениемR)
течет установившийся постоянный ток
и сопротивлениемR)
течет установившийся постоянный ток

 ,
где сопротивление источникаr → 0.
В момент размыкания сила тока
,
где сопротивление источникаr → 0.
В момент размыкания сила тока

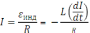 .
.
Отсюда
получаем дифференциальное уравнение

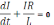 .
.
Решением
линейного дифференциального уравнения
первой степени (при t = 0 →
I
= I0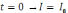 )
является функция
)
является функция 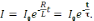 I
= I0e–tR/L
= I0e–t/τ.
I
= I0e–tR/L
= I0e–t/τ.
После
отключения источника ЭДС (t
= 0) сила тока в цепи не обращается
мгновенно в нуль, а убывает по
экспоненциальному закону. Скорость
убывания силы тока зависит от
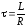
 – это время, в течение которого значение
тока размыкания уменьшается вe
раз (e
= 2,72). При замыкании цепи RLε
– это время, в течение которого значение
тока размыкания уменьшается вe
раз (e
= 2,72). При замыкании цепи RLε
 (ЭДС
ε, индуктивностьL
(ЭДС
ε, индуктивностьL ,
сопротивлениеR
,
сопротивлениеR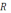 )
по закону Ома
)
по закону Ома
 .
Отсюда получаем неоднородное
дифференциальное уравнение
.
Отсюда получаем неоднородное
дифференциальное уравнение
 .
Значит, зависимость тока замыкания в
цепи с индуктивностью от времени
описывается формулойI
= I0(1
− e–tR/L)
= I0(1
− e–t/τ)
.
Значит, зависимость тока замыкания в
цепи с индуктивностью от времени
описывается формулойI
= I0(1
− e–tR/L)
= I0(1
− e–t/τ) ,
где
I
= 0 при t
= 0,
,
где
I
= 0 при t
= 0,
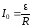
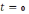 и
и
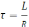 .
.
6.2. Расчетные формулы по теме «эм»
Ф = BS – магнитный поток, где B = const.
Rм
=
l
/
μ0μSN2 – магнитное сопротивление.
– магнитное сопротивление.
H
= B
/
μ0μ
 –
напряженность магнитного поля.
–
напряженность магнитного поля.
H ~ ФRм ~ IN – магнитное напряжение (Hl).
L
= ФN/I
– индуктивность (L
=  μ0μN2S
/l
).
μ0μN2S
/l
).
Диамагнетики:
–1
< x
< 0;
|x|
~
10–5;
B'
= μ0xH
 ~
0
→ B
=
μ0H,
~
0
→ B
=
μ0H,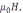 x
– магнитная
восприимчивость.
x
– магнитная
восприимчивость.
Парамагнетики:
0
< x
< 1;
x
~ 10–4;
B'
=
μ0xH
~ 0
→ B
= μ0H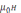 .
.
Ферромагнетики: μ ≈ 103–104; B' = μ0xH ≠ 0 → B = B0 + μ0J;
 μ0μH
=
μ0μH
=  μ0H
+
μ0xH
→
μ
μ0H
+
μ0xH
→
μ  =
1
+
x.
=
1
+
x.
W = ФI/2 = LI2/2 – энергия магнитного поля катушки.
ω
= W/V
= LI2/2V
=  μ0μH2/2
= BH/2
= B2/2μ0μ
μ0μH2/2
= BH/2
= B2/2μ0μ – плотность
энергии магнитного поля внутри катушки.
– плотность
энергии магнитного поля внутри катушки.
L = L1 + L2 – индуктивность двух индуктивно не связанных катушек.
L
= L1
+ L2
±

 – индуктивность индуктивно связанных
катушек.
– индуктивность индуктивно связанных
катушек.
1/L = 1/L1 + 1/L2 – параллельное соединение двух индуктивно не связанных катушек.
Трансформатор – устройство, преобразующее переменный ток одного напряжения в переменный ток другого напряжения. Потери Ф → 0. Примем
S1
=
S2,
μ1
=
μ 2,
Ф1
= Ф2,
B1
= B2,
H1
=
H2.
2,
Ф1
= Ф2,
B1
= B2,
H1
=
H2.
По закону полного тока Hl = I1N1; Hl = I2N2 → I1N1 = I2↑N2↓ – трансформатор понижающий (для сварки).
I1N1 = I2↓N2↑ – трансформатор для передачи энергии на расстояние.
Трансформатор на холостом ходу P = I1U1 = I2U2; U1N2 = U2N1.
εs = −dψ/dt = −d(LI)/dt – индукционная ЭДС, где εs – мгновенное значение индукционной ЭДС, ψ − потокосцепление, dψ/dt – производная потокосцепления по времени.
<εs>
= Δψ/Δt
–
среднее
значение индукционной ЭДС, где <ε
>
– среднее значение индукционной ЭДС,
Δψ
– изменение
потокосцепления,
 – промежуток времени, в течение которого
происходит потокосцепление.
– промежуток времени, в течение которого
происходит потокосцепление.
εs = −LdI/dt – ЭДС самоиндукции, где εs – мгновенное значение ЭДС самоиндукции, L – индуктивность, dI/dt – скорость изменения силы тока в контуре (производная силы тока по времени).
<εs> = LΔI/Δt – среднее значение ЭДС самоиндукции, где L – индуктивность контура, ΔI – изменение силы тока за промежуток времени Δt.
I = I0e–t/τ; I = I0(1 − e–t/τ) – токи при размыкании и при замыкании цепи, где τ = L/R – время релаксации (L – индуктивность, R – сопротивление), время, в течение которого значение тока уменьшается в e раз (e = 2,72).
