Тема 5.5. Уравнения плоскости. Взаимное расположение плоскостей

Литература: [1], гл.10, §1, 3, стр. 230–238; [3], гл 2, §2, стр. 46–54; [27], гл.7, §59-61, стр. 211-220.

Основные определения, теоремы и формулы

Уравнение плоскости, заданной точкой и некол- линеарными векторамиимеет вид

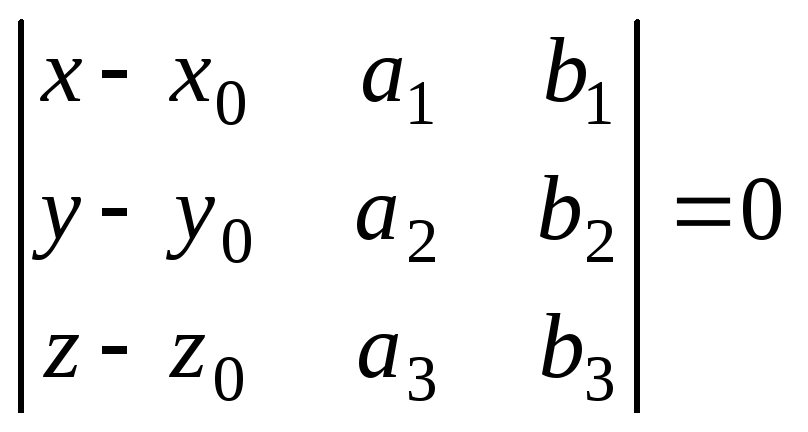или

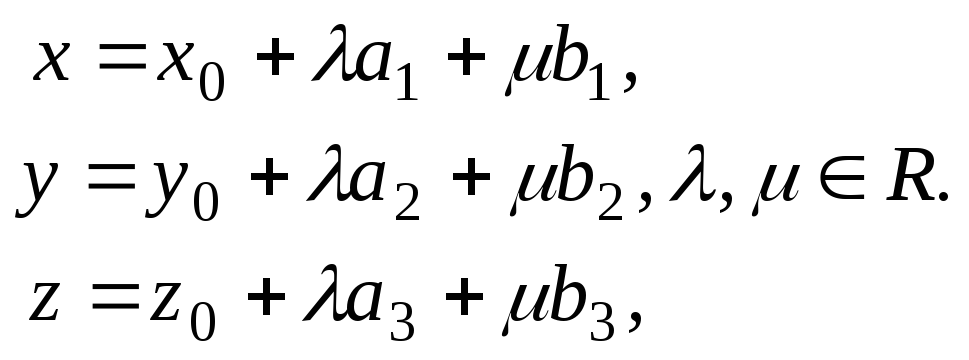
Последние уравнения называются параметрическими уравнениями.

Уравнение плоскости всегда можно привести к следующему виду:

где

которое называется общим уравнением плоскости.

Лемма.Векторпараллелен плоскости, заданной общим уравнениемтогда и только тогда, когда выполняется равенство

Пусть в аффинной системе координат даны две плоскости исвоими уравнениями:

Обозначим ,.

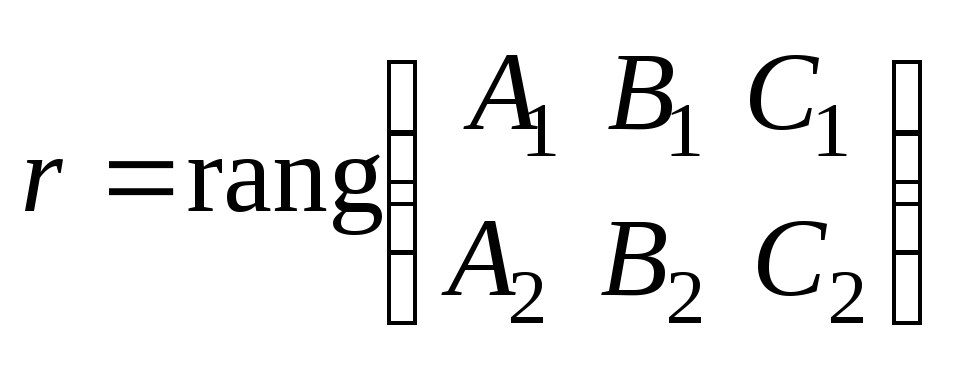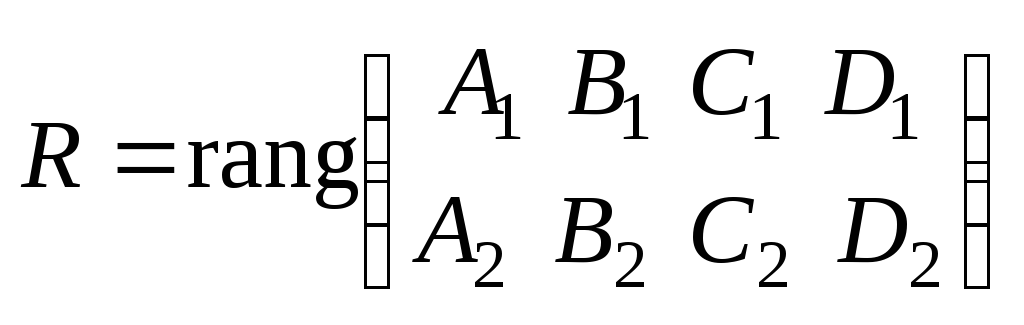Плоскости исовпадают тогда и только тогда, когда

Плоскости ипараллельны, но различны тогда и только тогда, когда

Плоскости ипересекаются по прямой тогда и только тогда, когда

Пример 1. Составить уравнение плоскости, проходящей через:

1) точку параллельно плоскости2) точкуи осьдве точкиипараллельно оси

Решение.1) Так как искомая плоскостьпараллельна плоскостито векторыи– направляющие векторы осейипараллельны ей. Поэтому плоскостьзадается точкойи векторамии:

или

2) Выберем на оси две точки, например,и. Так как осьпринадлежит плоскости, то и точкипринадлежат. Значит, плоскостьопределяется тремя точкамиили точкойи двумя векторамииЕе уравнение примет вид

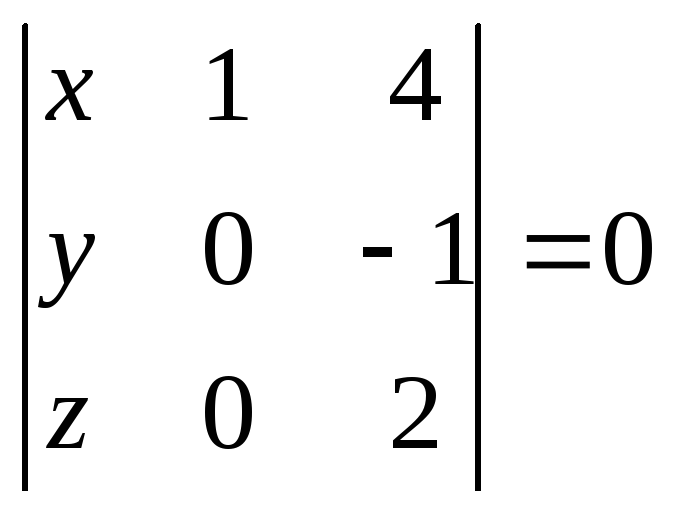или

Пример 2. Составить параметрические уравнения плоскости

Решение.1-й способ. Любые две из трех переменныхможно принять за независимые параметры. Положив, например,из уравнения плоскости найдемИскомые параметрические уравнения можно записать следующим образом:

2-й способ. Как известно, если плоскость задана общим уравнениемто векторы

принадлежат направляющему подпространству этой плоскости, и какие-либо два из них образуют базис этого пространства. Значит, векторы параллельны данной плоскости. Замечаем, что точкапринадлежит плоскости. Следовательно, плоскость можно задать точкойи векторамии:

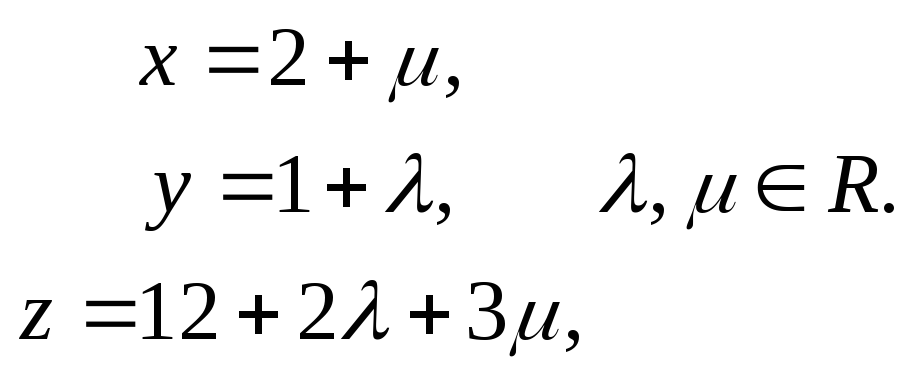
Вопросы для самоконтроля

1. Что называется направляющим подпространством плоскости?

2. Как записывается в векторном виде уравнение плоскости, заданной:

а) точкой и базисомнаправляющего подпространстваL,

б) тремя точками М₁, М₂, М₃, не лежащими на одной прямой,

в) точкой и прямойm, лежащими в этой плоскости

г) двумя пересекающимися прямыми аиb,

д) двумя параллельными прямыми аиb,

е) точкой и перпендикулярным вектором?

Предполагается, что в случаях в), г), д) прямые заданы точкой и направляющим вектором.

3. Как запишется уравнение плоскости в каждом из случаев а) – д) (см. вопрос 2), если в пространстве задана аффинная система координат О? Какой вид имеет уравнение плоскости в случае е (см. вопрос 2), если в пространстве задана прямоугольная декартова система координат?

4. Какой вид имеют векторное параметрическое уравнение и параметрические уравнения плоскости, заданной точкой и базисомнаправляющего подпространства?

5. Написать векторное и параметрические уравнения для каждой из координатных плоскостей системы координат О.

6. Что определяет в аффинной системе координат уравнение вида:

а) гдеA, B, C, D– вещественные числа,

б) гдеA, B, C, D – вещественные числа и

A² + B²+C² > 0?

7. Какое уравнение называется общим уравнением плоскости?

8. Как из параметрических уравнений плоскости получить её общее уравнение? Как решается обратная задача?

9. Как сформулировать критерий параллельности вектора (p₁,p₂,p₃) и плоскости, заданной уравнением?

10. Как расположен вектор (А, В, С) по отношению к плоскости, имеющей уравнениеесли система координат: а) аффинная, б) прямоугольная декартова? –

11. Плоскость в аффинной системе координат задана общим уравнением Как расположена плоскость по отношению к системе координат, если:

а) б)в)г)д)

12. Что определяется в аффинной системе координат каждым из следующих условий:

а) б)

в)

Здесь А, В, С, D– вещественные числа иА² + В² + С² > 0.

13. Как выяснить, имеет ли плоскость, заданная общим уравнением пересечение с внутренностью тетраэдраABCD, гдеА(а₁, а₂, а₃), В(b₁, b₂, b₃), C(c₁, c₂, c₃), D(d₁, d₂, d₃)?

14. Как выяснить взаимное расположение двух плоскостей, заданных своими общими уравнениями А₁x + B₁y + C₁z + D₁ = 0 и

А₂x + B₂y + C₂z + D₂ =0?

15. Какой вид имеет уравнение произвольной плоскости:

а) параллельной плоскости

б) проходящей через фиксированную точку

в) параллельной данному вектору

Задачи

1. Написать уравнение плоскости, которая:

а) параллельна координатной плоскости 0xzи проходит через точкуА(2, –5,3),

б) содержит ось аппликат и точку В(–3, 1, –2),

в) параллельна оси абсцисс и проходит через точки С(4, 0, –2) и

D(5, 1, 7).

2. Написать параметрические уравнения плоскости, которая проходит через точку А(2, –1, 3) параллельно плоскости, заданной уравнениемПерейти от полученных параметрических уравнений к общему уравнению плоскости. В какой системе координат решается задача?

3. В аффинной системе координат две плоскости заданы уравнениями и Записать систему неравенств, определяющую тот двугранный угол, образованный этими плоскостями, которому принадлежит:

а) начало координат, б) точка А(3, –4, 3).

4. При каких значениях параметров иплоскости, заданные в аффинной системе координат уравнениямии

а) параллельны, б) совпадают, в) пересекаются?

5. Через точку А(–5, 16, 12) проведены две плоскости, одна из которых содержит ось абсцисс, вторая – ось ординат. Найти косинус угла между этими плоскостями.

6. Написать уравнение плоскости, проходящей через начало координат и перпендикулярной к линии пересечения плоскостей, заданных уравнениями и

Домашнее задание

1. Написать параметрические уравнения плоскости, заданной в аффинной системе координат общим уравнением:

а)

б)

2. Найти координаты точки, принадлежащей плоскости, и координаты двух векторов, образующих базис направляющего подпространства этой плоскости.

3. Написать общее уравнение плоскости, заданной в аффинной системе координат параметрическими уравнениями:

а)

б)

4. Найти основание перпендикуляра, проведенного из точки Р(1, 3, 5) к прямой, по которой пересекаются плоскостии

5. Даны две точки А(1, 3, –2) иВ(7, –4, 4). Через точкуВ проведена плоскость, перпендикулярная прямойАВ. Написать ее уравнение.

6. Найти множество всех точек пространства, каждая из которых равноудалена от точек А(2, –1, 3) иВ(4, 5, –3).

Задачи повышенной трудности

1. Плоскость вместе с координатными плоскостями образует некоторый тетраэдр. Найти ребро куба, который можно поместить внутрь этого тетраэдра так, чтобы три грани его лежали на координатных плоскостях, а вершина, противоположная началу координат, лежала в данной плоскости.

2. Написать уравнение плоскости, перпендикулярной плоскости и пересекающей ее по прямой, лежащей в координатной плоскости