Загальна схема дослідження функції

 

Наведемо схему, за якою доцільно досліджувати графік функції.

1) Знайти область визначення, перевірити функцію на парність, непарність, періодичність.

2) Визначити область неперервності та точки розриву.

3) Знайти асимптоти графіка функції.

4) Знайти критичні точки першого роду, визначити проміжки зростання і спадання функції, знайти точки локального екстремуму.

5) Знайти точки перегину, проміжки опуклості і вгнутості.

6) Знайти точки перетину графіка з віссю ординат; точки перетину з віссю абсцис (якщо це можливо); інші контрольні точки.

7) За одержаними результатами побудувати  ескіз графіка функції.

 

3.8 Приклади розв’язування типових завдань з дослідження функцій, заданих явно

 

Приклад 3.40. Дослідити функцію 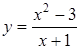та побудувати її графік.

Розв’язання.

1) Функція визначена для всіх . Функція загального виду, оскільки. Функція не є періодичною.

2) В точці функція має розрив.

Оскільки 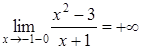,,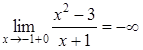 то точкає точкою розриву другого роду типу „нескінченний стрибок”.

3,а) Враховуючи дослідження пункту 2), робимо висновок, що пряма є вертикальною асимптотою.

3,б) Шукаємо похилі асимптоти у вигляді . Тут,  відповідають випадку , а,  - випадку . Знайдемо невідомі коефіцієнти,  за формулами (3.24), (3.25)

 

,

 

.

 

Отже, одна і та ж сама похила асимптота як при, так і при.

4) Для визначення інтервалів монотонності та локальних екстремумів обчислимо спочатку похідну

 

.

 

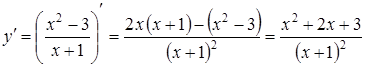Знайдемо проміжки знакосталості для .

Рівняння дійсних коренів не має, причому. Врахувавши те, що знаменник, робимо висновок, щона кожному з проміжків неперервності. Отже дана функція зростає приі при. Точок локального екстремуму немає.

5) Знайдемо проміжки опуклості (вгнутості).

Для цього обчислимо спочатку :

 

.

 

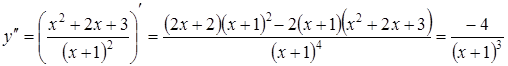Рис. 3.15

Знайдемо проміжки знакосталості для . За методом інтервалів отримуємо, щопри- тут графік функції вгнутий, тапри- тут графік функції опуклий. В самій точціфункція невизначена, тому точки перегину немає. 6) Знайдемо точки перетину графіка з координатними осями. Графік функції перетинає вісь абсцис, якщо , отже, маємо точки:. Графік перетинає вісь ординат, якщо, маємо точку.

 

7) У відповідності з проведеним дослідженням будуємо ескіз графіка даної функції (див. рис. 3.15).

Приклад 3.41. Дослідити функцію та побудувати її графік.

Розв’язання.

1) Функція визначена на всій числовій осі. Функція не є парною, оскільки ; не є непарною, оскільки. Функція не є періодичною.

2) Функція неперервна на всій числовій осі.

3,а) Оскільки функція є неперервною, вертикальних асимптот немає.

3,б) Шукаємо похилі асимптоти у вигляді . Тут,  відповідають випадку , а,  - випадку . Знайдемо невідомі коефіцієнти,  за формулами (3.24), (3.25).

.

 

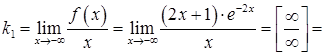
Отже, похилої асимптоти при (зліва) не існує.

,

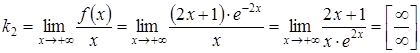за правилом Лопіталя:

;

 

,

 

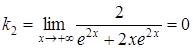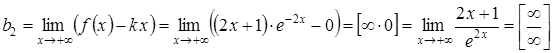за правилом Лопіталя:

.

 

Отже,  похила асимптота при (права горизонтальна асимптота).

4) Для визначення інтервалів монотонності та локальних екстремумів спочатку обчислимо похідну

.

Знайдемо проміжки знакосталості для .

Рівняння має єдиний корінь(єдина критична точка). За методом інтервалів отримуємо, щопри- на цьому інтервалі функція зростає іпри- тут функція спадає. Оскільки при переході через точкупохідна змінює знак з „+” на „”, то є точкою локального максимуму,.

5) Визначимо інтервали опуклості (вгнутості) і точки перегину.

Для цього обчислимо спочатку :

.

 

Знайдемо проміжки знакосталості для .

Рівняння має єдиний корінь. За методом інтервалів отримуємо, що при,- тому на цьому інтервалі графік функції опуклий; при,- графік угнутий.

Оскільки при переході через точку друга похідна змінює знак, тоє точкою перегину;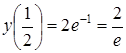. Перегин:.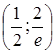

6) Знайдемо точки перетину графіка з координатними осями.

 

Рис. 3.16

Графік функції перетинає вісь абсцис, якщо ,  отже, маємо точку . Графік перетинає вісь ординат, якщо , маємо точку.

7) За результатами дослідження будуємо ескіз графіка даної функції (рис. 3.16).

Приклад 3.42. Дослідити функцію та побудувати її графік.

Розв’язання.

1) Функція визначена для всіх . Функція не є парною, оскільки; не є непарною, оскільки. Функція не є періодичною.

2) Функція неперервна на кожному з інтервалів ,. В точціфункція має розрив.

Оскільки

 

, ,

 

то точка є точкою розриву другого роду типу „нескінченний стрибок”.

3,а) Враховуючи пункт 2), робимо висновок, що пряма є вертикальною асимптотою.

3,б) Шукаємо похилі асимптоти у вигляді . Тут,  відповідають випадку , а,  - випадку . Знайдемо невідомі коефіцієнти,  за формулами (3.24), (3.25).

 

;

 

 

.

 

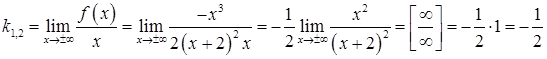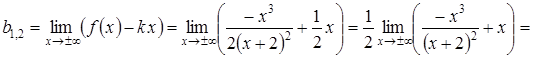
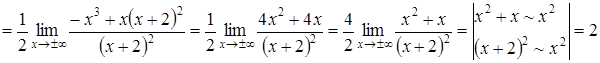Отже, пряма є похилою асимптотою як при, так і при.

Знайдемо точку перетину графіка (якщо це можливо) з похилою асимптотою:

, .

 

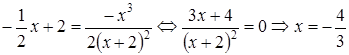Маємо точку перетину .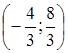

4) Визначимо інтервали монотонності та точки локального екстремуму. Спочатку обчислимо похідну

 

.

 

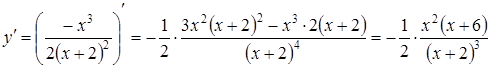Знайдемо проміжки знакосталості для за методом інтервалів.

Рівняння має кореніта(критичні точки першого роду). Похідна не існує в точці, але оскільки ця точка не належить області визначення, то вона не є критичною (у ній не може бути екстремуму).

За методом інтервалів складаємо таблицю зміни знаків похідної

 

x						0
		0	+	не існує		0	
y		min 6,75		не існує

 

У точці функція має локальний мінімум, оскільки при переході значень аргументу через неї похідна змінює знак з „” на „+”, .

У точці функція не має локального екстремуму.

5) Визначимо інтервали опуклості (вгнутості) і точки перегину.

Для цього обчислимо спочатку другу похідну :

 

 

.

 

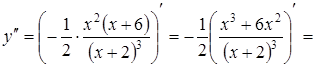
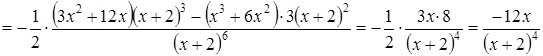Знайдемо проміжки знакосталості для .

Похідна дорівнює нулю при (критична точка другого роду) і не існує при(протене є критичною точкою, тому що функція в ній не існує).

За методом інтервалів складаємо таблицю зміни знаків похідної

 

x
	+	не існує	+	0	
y		не існує		перегин

 

При ,, тому на цих інтервалах графік функції вгнутий; приграфік опуклий.

Оскільки при переході значень аргументу через точку друга похідна змінює знак, тоє точкою перегину;. Отже, перегин.

6) Точка перетину графіка з віссю абсцис (ординат) вже знайдена.

7) За результатами дослідження будуємо ескіз графіка даної функції (рис. 3.17).

 

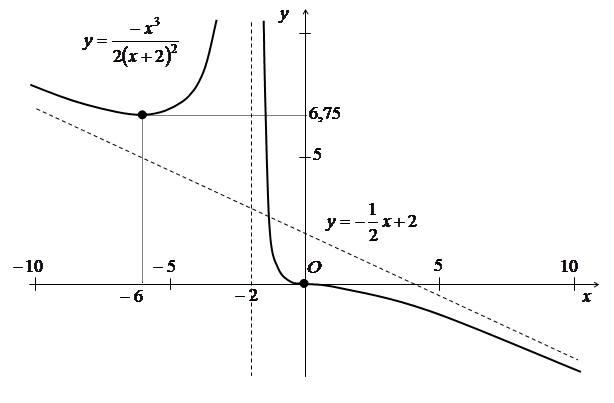
Рис. 3.17
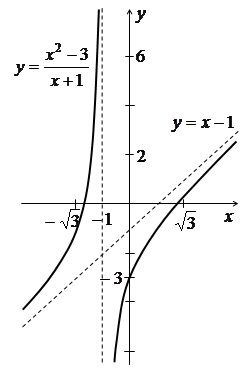