Практичне правило інтегрування раціональних дробів.

1. Якщо дріб неправильний, то виділяємо цілу частину шляхом ділення чисельника на знаменник. Тоді переходимо до суми інтегралів від многочлена і правильного раціонального дробу.

2. Знаменник правильного дробу розвиваємо на незвідні множники.

3. Правильний дріб подаємо у вигляді суми елементарних дробів із невизначеними коефіцієнтами з врахуванням кратності коренів його знаменника.

4. Звівши отримані дроби до спільного знаменника прирівнюємо спочатку чисельники, а потім і коефіцієнти при невідомих в однакових степенях. Одержуємо систему лінійних рівнянь для знаходження коефіцієнтів розвинення.

Приклад. Обчислити .

Розв’язування

Степінь знаменника підінтегрального дробу більший за степінь чисельника – даний дріб є правильним. Оскільки , то знаменник підінтегрального дробу має дійсний корінькратності два. Тому

.

Зводячи праву частину до спільного знаменника, маємо:

.

Оскільки найстарший степінь змінної у правій частині рівності перший, отримуємо систему:

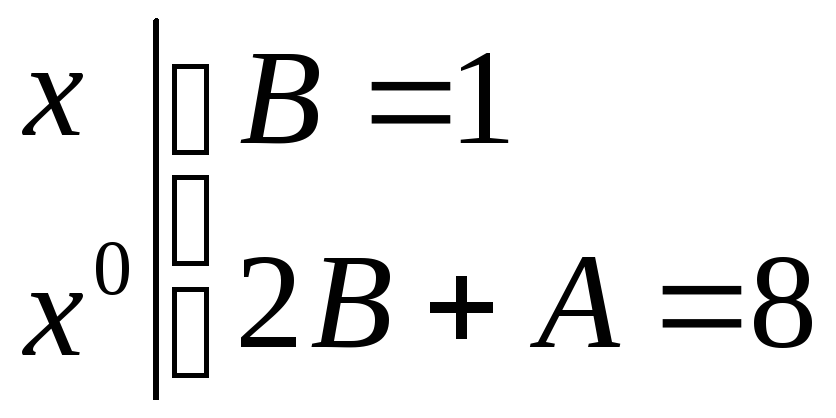
Отже .

Тому:

==

Приклад. Обчислити .

Розв’язування

Оскільки даний підінтегральний дріб правильний і знаменник має один простий дійсний корінь та один простий комплексний корінь, то:

.

Зводячи праву частину до спільного знаменника, маємо:

.

Оскільки найстарший степінь змінної у правій частині рівності другий, отримуємо систему:

.

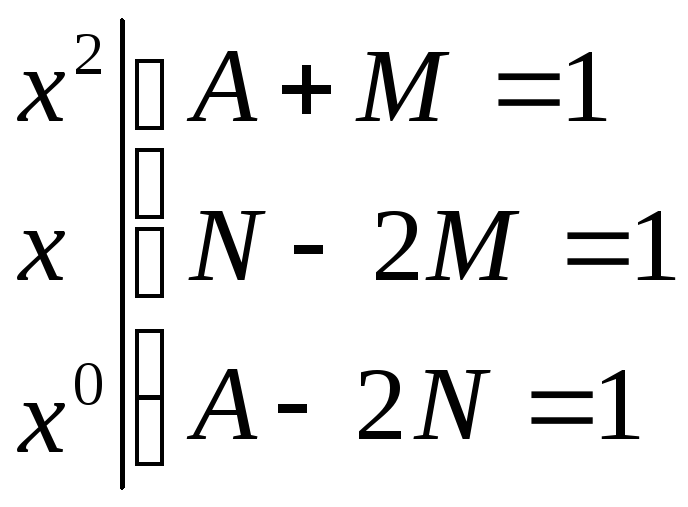
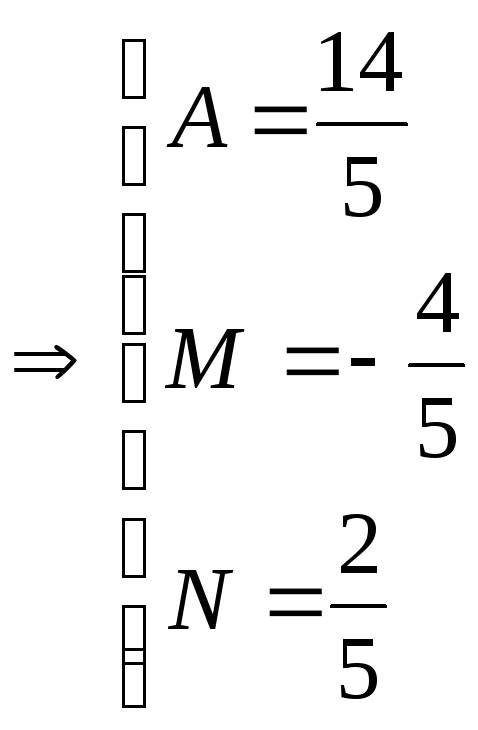Отже .

Тому:

=== =.

3. Інтегрування за допомогою підстановки

Нехай для функції важко підібрати первісну, але відомо, що вона існує.

Досить часто інтеграл можна спростити, ввівши нову зміннуі поклавши. Тоді має місце співвідношення:

Введенням нової змінної можна звести інтеграл до табличного.

Приклад. Обчислити .

Розв’язування

Введемо нову змінну , тоді,і===

Наведемо деякі найбільш уживані підстановки:

Підінтегральна функція	Підстановка
, де	, де - спільний знаменник дробів
, де	, де - спільний знаменник дробів
	а) якщо , то виділяють повний квадрат виду, тоді; або повний квадрат виду, тоді; б) якщо , то виділяють повний квадрат видуабо, тоді
	а) якщо , то, де- спільний знаменникта; б) якщо , то, де- знаменник дробу; в) якщо , то, де- знаменник дробу
	а) універсальна тригонометрична підстановка - ; б) якщо підінтегральна функція змінює свій знак при зміні знака , то; в) якщо підінтегральна функція змінює свій знак при зміні знака , то.

Приклад. Обчислити інтеграл .

Розв’язування

==== =

Приклад. Обчислити інтеграл .

Розв’язування

===== ==== ==

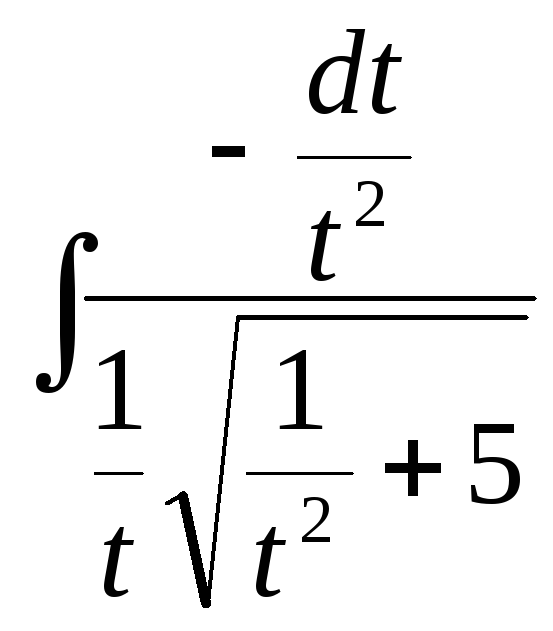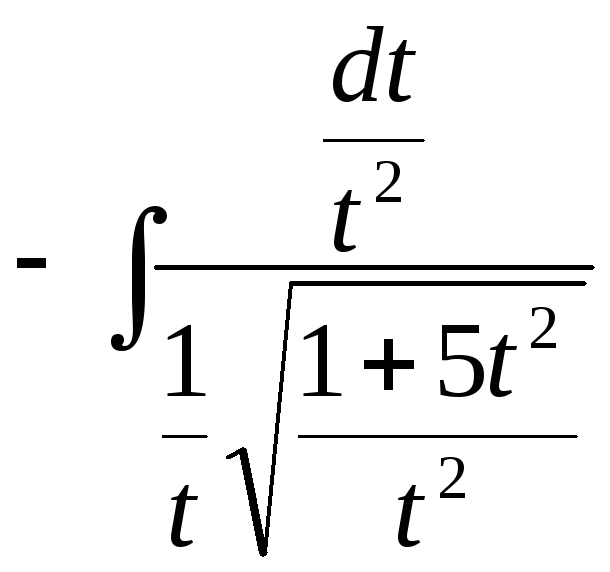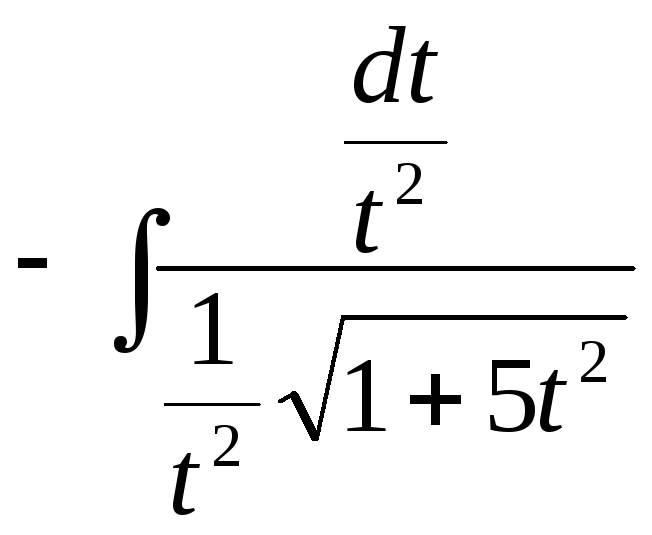ЕЛЕМЕНТИ ТЕОРІЇ ФУНКЦІЇ БАГАТЬОХ ЗМІННИХ

Змінна величина u називається функцією n змінних величин x, y, z, … , t (аргументів), якщо при заданих значеннях цих змінних величина u приймає єдине значення. Позначення: функція двох змінних: u=f(x, y), функція трьох змінних: u=F(x, y, z ), функція n змінних: u=φ(x, y, z, … , t). Графіком функції двох змінних u=f(x, y) є поверхня, яка задається рівнянням u-f(x, y) =0

Способи задання функції

1. Табличний спосіб

Значення аргументів розташовані по верхньому та лівому краях таблиці, а значення функції знаходиться на перетині відповідного рядка та стовпця.

Наприклад, таблиця функції F- розподілу Фішера (див. додаток В).

2. Аналітичний спосіб.

Функція багатьох змінних задається однією або декількома формулами. Наприклад,

u=xy²,

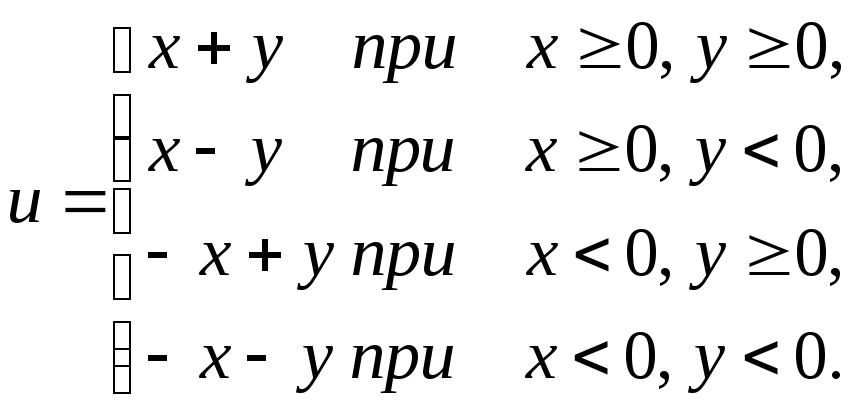
Причому, множину значень аргументів, при яких формула має зміст, називають областю існування функції.

Диференціювання функції багатьох змінних

Частинна похідна функції багатьох змінних u=f(x, y, z, … , t) за однією із змінних, наприклад за x (позначення ,,) визначається рівністю:

;

в цьому випадку приріст отримує лише одна із незалежних змінних, а решта змінних вважаються константами. Функція n змінних має n частинних похідних: .

Зауваження.

Частинна похідна знаходиться за правилами диференціювання функції однієї змінної.

Приклад. Знайти частинні похідні функції .

Приклад. Знайти частинні похідні функції

Знаходимо, ;.

Взагалі кажучи, частинні похідні є функціями від змінних x, y, z,…,t. Тому від них знову можна знаходити частинні похідні. Це означає, що частинних похідних другого порядку, наприклад від функції двох змінних , є чотири. Частинні похідні другого порядку позначаються так:

1) , тут функція u диференціюється послідовно два рази заx;

2) , в цьому випадку функція u диференціюється спочатку за змінною, а потім за змінноюy.

3) , тут функція диференціюється спочатку заy, а потім за x.

4) , в цьому випадку функція диференціюється двічі заy.

Частинні похідні (2) та (3) називаються мішаними частинними похідними.

Зауваження! Неперервні функції мають рівні мішані частинні похідні.

Частинні похідні другого порядку знову можна диференціювати як за x, так і за y. В результаті отримуємо похідні третього порядку. Очевидно, що їх буде вісім. Наприклад, . В даному випадку функція диференціюється послідовно двічі заx, а потім за y.

Приклад. Знайти частинні похідні другого порядку від функції .