Розв’язування

Середня вартість одиниці продукції визначається діленням загальної вартості на кількість вироблених одиниць:

Знайдемо першу похідну цієї функції і прирівняємо її до нуля. Маємо:

. Звідки .

Оскільки , а, то відповідний мінімум досягається в точці.

ЕЛЕМЕНТИ ІНТЕГРАЛЬНОГО ЧИСЛЕННЯ

Поняття первісної функції та невизначеного інтеграла

Функція називаєтьсяпервісною або примітивною для функції , якщодиференційовна і.

Якщо - первісна для функції, то всі первісні цієї функції відрізняються лише на константу.

Множину усіх первісних для функції називаютьневизначеним інтегралом і позначають .

Таблицю інтегралів від елементарних функцій наведено у додатку Б.

Властивості невизначеного інтеграла

1.

2.

3. , де

4.

5. , де

6. Якщо , то, де

7. Якщо , то, де.

8. Якщо , то

Приклад. Граничний дохід фірми описується функцією , де- кількість виробленої продукції. Якою буде функція сумарного доходу фірми, якщо нульовий випуск продукції дає нульовий дохід?

Розв’язування

За означенням граничного доходу маємо:

.

Враховуючи умову, що , обчислимо константу:

Отже, сумарний дохід фірми .

Приклад. Нехай гранична ціна за продану продукцію описується функцією , де- кількість проданої продукції. Якою буде загальна функція ціни за продану продукцію, якщо ціна 100 одиниць продукції дорівнює 40000 грн.?

Розв’язування

За означенням граничної ціни

.

З умови маємо:.

Отже, ціна продукції має вигляд: .

Основні прийоми інтегрування

1. Інтегрування частинами

Якщо функції тадиференційовні на деякому проміжку і на цьому проміжку існує, то існуєі має місце рівність:

.

Цей прийом застосовується у випадках, коли підінтегральна функція така:

а) ,,,,(тоді,і т.д.) ;

б) ,,,,(тоді,і т.д.).

в) ,,,,(тоді);

г) ,.

Приклад. Обчислити значення інтеграла.

Розв’язування

===

2. Інтегрування раціональних дробів

Функція, що має вигляд , де,, називається дробово-раціональною. Очевидно, що у випадку, коли, дріб є неправильним і з нього можна виділити цілу частину шляхом ділення чисельника даного дробу на знаменник. Тоді, де- многочлен степеня, а- многочлен меншого степеня, ніж.

Оскільки інтегрування многочленів є досить простим, то достатньо навчитись інтегрувати правильні дроби. Прийоми інтегрування правильних дробів зводяться до інтегрування чотирьох можливих елементарних дробів:

І. ,	ІІ. ,
ІІІ. ,	IV. ,

де рівняння не має дійсних коренів.

Дроби І та ІІ інтегруються за допомогою підстановки . Тому

І. ;

ІІ.

Для того, щоб проінтегрувати дріб ІІІ, виділимо у його знаменнику повний квадрат та обчислимо диференціал знаменника . Слід відмітити, що оскількирівняння не має дійсних коренів, то . Виділимо в чисельнику дробу ІІІ диференціал знаменника і скористаємося розвиненням останнього у повний квадрат. Маємо:

==

==

==

=.

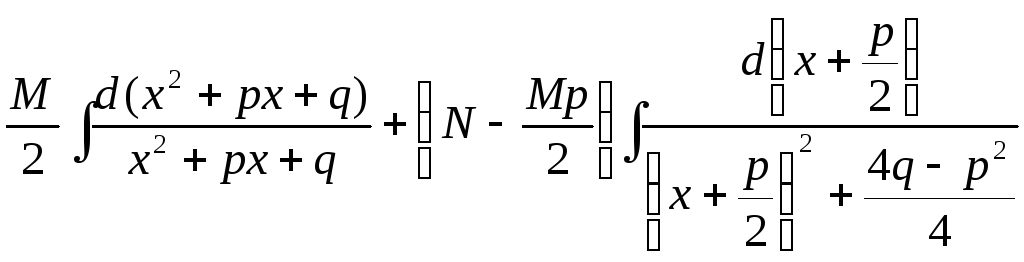Таким чином, =

Випадок інтеграла від елементарного дробу IV дещо складніший, але допускає інтегрування із застосуванням так званих рекурентних формул. Позначимо ,,. Тоді

==.

Перший інтеграл обчислюється за допомогою заміни

.

Для обчислення другого інтеграла виведемо рекурентну формулу, що дозволяє на кожному кроці понижувати степінь знаменника на одиницю. Введемо позначення .

Диференціюванням можна довести справедливість формули:

. (5)

Застосовуючи послідовно раз формулу (5), інтегралзводиться до табличного інтеграла.

Інтегрування правильного раціонального дробу зводиться до інтегрування елементарних дробівза допомогою таких теорем.

Якщо - правильний раціональний дріб і- дійсний корінь знаменника кратності, то

=, ()

де - дійсні числа, а.

Якщо - правильний раціональний дріб і- комплексний корінь знаменника кратності, то

=, (6)

де - дійсні числа,

Зауваження! 1. Число називається коренем многочлена, якщо.

2. Число називається простим коренем многочлена, якщо він ділиться наі не ділиться на.

3. Число називається коренем многочленакратності, якщо він ділиться наі не ділиться на.