Правила диференціювання

Нехай ми маємо дві диференційовні функції U(x) та V(x) (в скороченому записі U та V), тоді

1.

2.

3. , деV0.

4. Похідна складеної функції y=f((x)) обчислюється: .

Похідні елементарних функцій наведені в додатку А.

5. Нехай маємо функцію . Щоб знайти похідну цієї функції, потрібно її прологарифмувати та знайти похідну даного виразу, пам’ятаючи, щоє складеною функцією. Тобто,

. Тоді . Звідки маємо:

6. Нехай функція задана неявно:. Для того, щоб знайти похідну функції, потрібно спочатку визначити похідну виразу, пам’ятаючи, щоє функцією від змінної, а потім знайти саме значення.

Приклад. Знайти похідну складеної функції .

Розв’язування

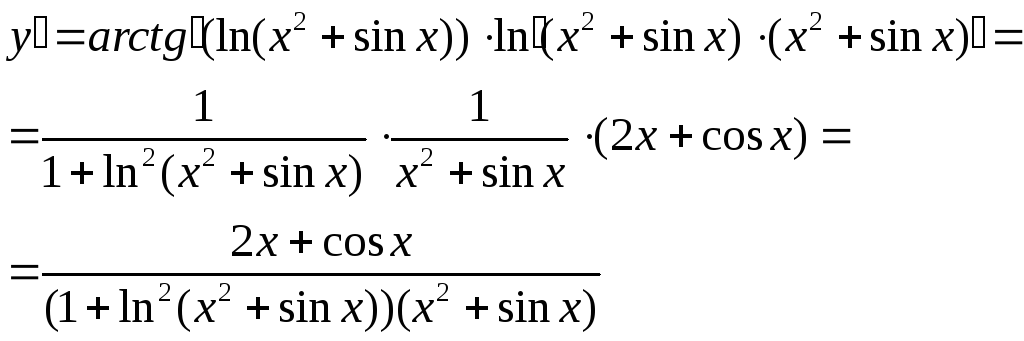
Приклад Знайти похідну складеної функції .

Розв’язування

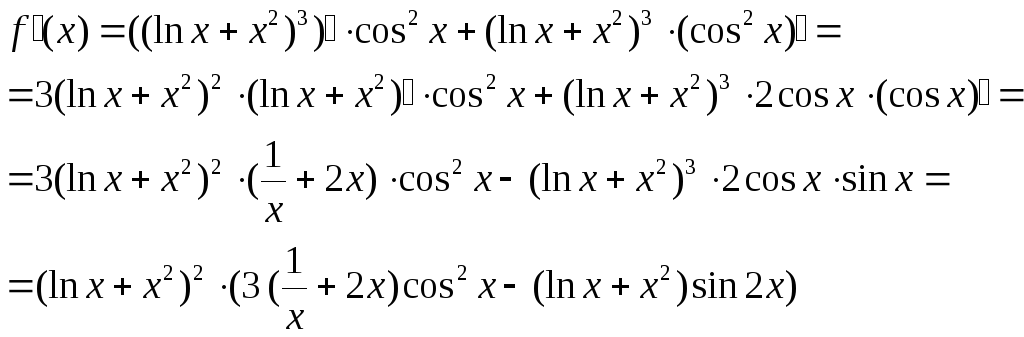
Приклад. Знайти похідну функції .

Розв’язування

. Звідки . Тому

Приклад. Знайти похідну функції заданої неявно .

Розв’язування

. Маємо . Звідки

Визначення характеру монотонності функції, знаходження

максимуму та мінімуму функції

Теорема. Для того, щоб диференційовна на проміжку (a, b) функція у=f(х) була незростаючою (неспадною) на цьому проміжку, необхідно і достатньо, щоб в усіх його точках похідна була б недодатною (невід’ємною). Тобто ().

У випадку, коли () функція буде спадною (зростаючою).

Нехай маємо функцію у=f(х), визначену на відрізку [a, b], та деякий окіл точки x₀, що належить вказаному відрізку. Тоді точка x₀ називається точкою максимуму (мінімуму) функції, якщо справедлива нерівність: (). Причому, x₀ буде точкою строгого максимуму (строгого мінімуму), якщо:(). Точки максимуму та мінімуму називаютьточками екстремуму або екстремальними точками, а відповідні значення функції в цих точках - екстремумами.

Теорема (необхідна умова екстремуму функції). Якщо точка x₀ є точкою екстремуму у=f(х), то похідна цієї функції в точці x₀ або не існує, або дорівнює нулю.

Теорема (достатня умова існування екстремуму). Нехай функція у=f(х) – неперервна і диференційовна на деякому проміжку. Якщо похідна функції змінює свій знак при переході через точкуx₀, то точка x₀ - точка екстремуму. Причому, якщо похідна змінює свій знак з мінуса на плюс (з плюса на мінус), то x₀ – точка мінімуму (максимуму).

Приклад . Знайти всі максимуми і мінімуми функції .

Розв’язування

1)Дана функція диференційовна на всій числовій осі і .

2) Знайдемо всі „підозрілі” на екстремум точки шляхом розв’язання рівняння виду , тобто. Це рівняння має єдиний корінь.

3) Відмітимо знайдений корінь на числовій осі:

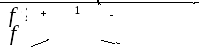
Вказаний корінь розбиває числову вісь на два проміжки та. Виберемо на проміжкудовільну точку, наприклад, х=0, і підставимо її значення у вираз похідної. Тобто,. Аналогічним чином виберемо довільну точку на проміжку. Нехай це буде х=2, підставивши вибране значення у похідну, маємо:. Це означає, що при переході через точку х=1 похідна функції змінює свій знак з плюса на мінус, тобто вказане значення дає максимум. Інших екстремумів у даної функції немає.

Приклад. Знайти всі максимуми та мінімуми функції .

Розв’язування

1) Дана функція диференційовна на всій числовій осі. Маємо:

2) Знайдемо всі критичні точки функції, розв’язавши рівняння . Оскільки добуток дорівнює нулю у випадку, коли хоча б один із множників дорівнює нулю, отримуємо три корені:,,.

3) Відмітимо знайдені корені на числовій осі:

Знайдені корені розбивають числову вісь на чотири проміжки: ,,,. На кожному із проміжків виберемо довільну точку, підставимо вибрані значення у вираз похідної та з’ясуємо знак похідної на цих проміжках, що відображається на схемі :,,

, .

Оскільки похідна функції при переході через точку змінює свій знак з плюса на мінус, то в даній точці маємо максимальне значення, яке дорівнює. При переході через точкупохідна змінює свій знак з мінуса на плюс, отже в цій точці маємо мінімальне значення, яке дорівнює.

Приклад. (Мінімізація середньої вартості одиниці продукції). Загальна вартість вироблених одиниць продукту А визначається функцією(у грн.). Скільки одиницьпродукції треба випускати, щоб мінімізувати середню вартість одиниці продукції?