29.Характеристика флуктуационной помехи.

Флуктуационная помеха (шум) - Вид помех, которые присутствуют практически во всех реальных каналах связи и представляют собой случайный процесс с нормальным распределением. Основным источником флуктационного шума является беспорядочное тепловое движение электронов в проводнике, вызывающее случайную разность потенциалов на его концах.

Для анализа шумовой помехи используется модель «белого шума» с неограниченным набором частот.

Модель основывается на нормальном законе распределения вероятности. Вычисление нормального закона может производиться с применением распределения.

дифференциальный вид.

P(Un) – Текущее значение амплитуды шумовой помехи

Ucp – Среднее значение амплитуды шумовой помехи

– Средне квадратичное отклонение, характеризующее амплитуду пе

ременной составляющей помехи

30.Характеристика импульсной помехи.

Импульсными помехами называют случайные кратковременные искажения амплитуды сигнала.

Импульсная помеха описывается формой линии и функциями распределения пиковой амплитуды и скважности. Скважность характеризует "плотность" импульсных помех в сигнале и определяется как отношение длительности импульсной помехи к средней величине длительности интервала между соседними помехами.

Импульсный шум представляет собой последовательность импульсов произвольной длительности и амплитуды, следующих друг за другом через случайные промежутки времени.

Он отличается от непрерывного шума тем, что длительность импульсов шума значительно меньше промежутков между ними, поэтому появление каждого импульса рассматривается как независимое событие.

Число независимо возникающих импульсов в течение любого промежутка времени подчиняется пуассоновскому распределению:

,

где Р(n) — вероятность появления n импульсов за время Т, а γ — среднее число импульсов в единицу времени.

Прохождение импульсного шума через полосовую цепь приводит к размыванию импульсов, т.е. к расширению импульсов и слиянию их в непрерывный шум.

При этом значение его пикового уровня пропорционально ширине полосы пропускания, а значение среднего уровня – корню квадратному из полосы частот.

31.Методика расчета величины кодового перехода/расстояния d.

Кодовое расстояние – кол-во разрядов, в которых одна комбинация отличается от другой. Форма кодового перехода связывает кодовое расстояние d корректирующей способностью. d=r+s+1; r-кол-во обнаруживаемых ошибок кода, s-кол-во исправленных ошибок кода.

Дано:

Tбк=10мс – время передачи информ. блока

fсп=0,1 1/c – частота следования случайной помехи

d - ?

i-ошибок

Вероятность правильного прохождения:

Рпр=Р(i=0)=e^(0,001*0,1)=0,999

Pош=1- Рпр=1-0,999=0,001

Вес ошибки: W=P(i)/Pош

W=ΣW(i)=P(i)/Pош=0,85

i 0 1 2 3

P ----- 0,001 5E-07 1,7E-10

W ----- 0,999 0,0005 1,7E-07

Основной вес у одиночной ошибки, поэтому код должен обнаружить одиночную ошибку.

1)d≠r+1=2

2)d=r+s+1=3

32.Процедура построения циклического кода (ЦК) d=3.

Цикл. коды строятся на базе цикл. свойств квадратных матриц или на основе образующего многочленов. Особенность: Р(х) обладает свойством простого числа . Исх. комбин. при кодировании умножается на Р(х) .Если на примнике код не делится на р(х),в коде ошибка. Все циклические коды относятся к блочным разделимым кодам – делятся на информационные и контрольные. Циклический код d=3(r=1,S=1) d=2S+1; блочный разделимый код: d=r+S+1; n=m+k; К.Хемминга, для ЦК ;- ЦК

n	1	3	7	15	31	63	127	255
k	0	1	4	11	26	57	120	247
m	1	2	3	4	5	6	7	8

Процедура построения : Представление циклического кода – представление циклического двоичного числа в виде многочлена фиктивной переменной х.

Позиции 1 2 3 4 5 6 7 8

G=1 0 1 0 1 1 0 1 g(x)-неизбыт.комб-ция , x – фиктивная переменная.

Степени 7 6 5 4 3 2 1 0

, для данного кода:

, Q-целая часть, -остаток

Существуют 2 способа построения ЦК:

1)F(x) Умножим левую и правую часть исходного уравнения на P(x)

- на практике

2)

Пример: закодировать кодовую комбинацию. g(x)=1011=

d=3 ; . Для k=4 (m=3, n=7).

Для этого кода соответствует образующий многочлен из таблицы:

. Этому коду соответствует многочлен:

(*)(по первому способу)

32.Процедура построения циклического кода (ЦК) d=3.(обр,сторона

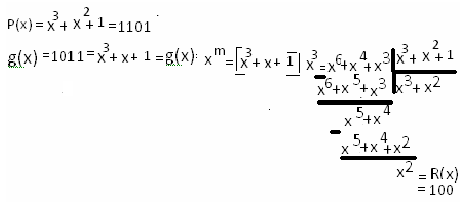
По (*),1011-g(x) 100-R(x)

Выполняют эти операции – микросхемы. Циклический код записывается в виде матрицы: единич инф. м-ца и транспон: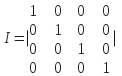

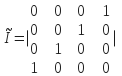
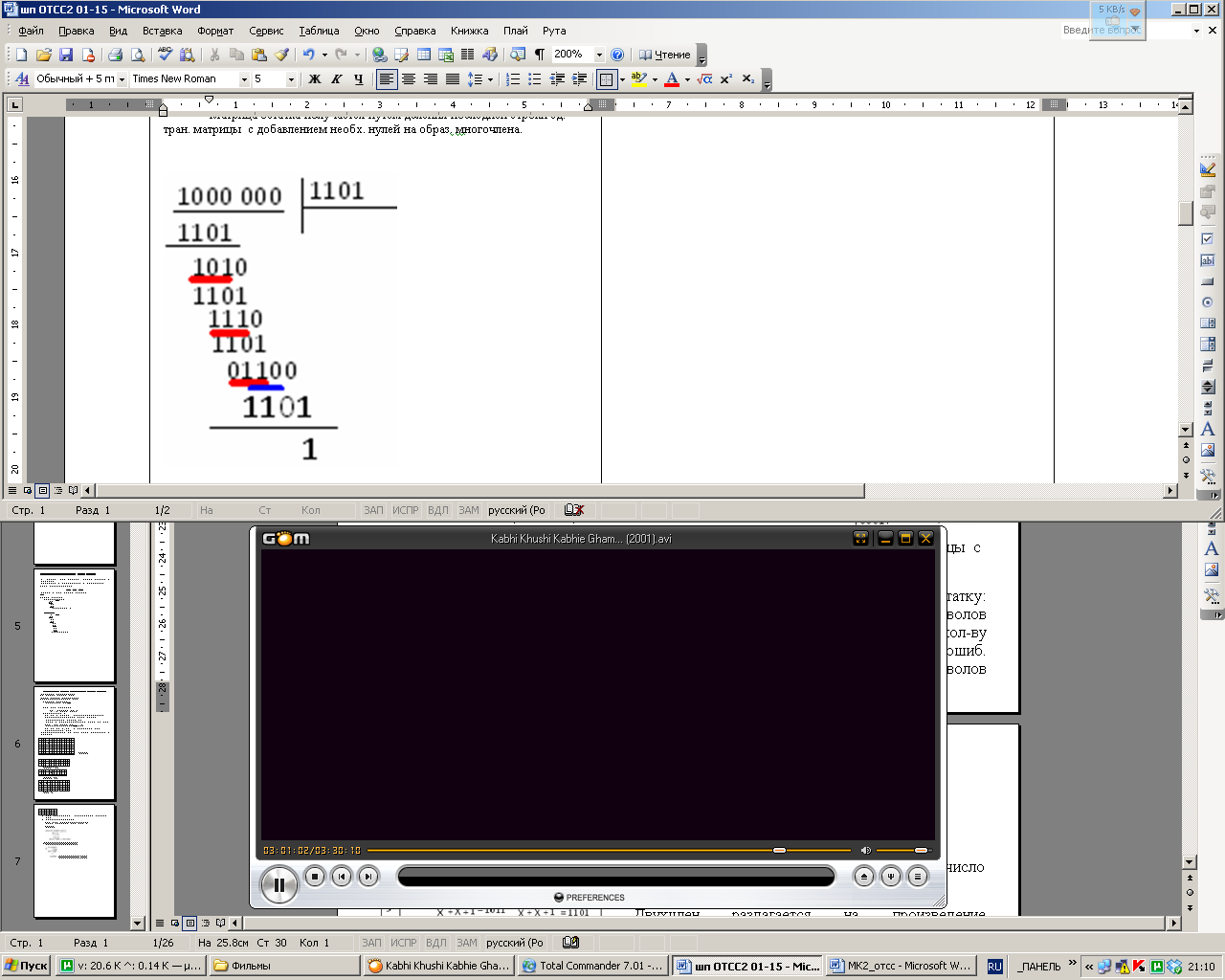
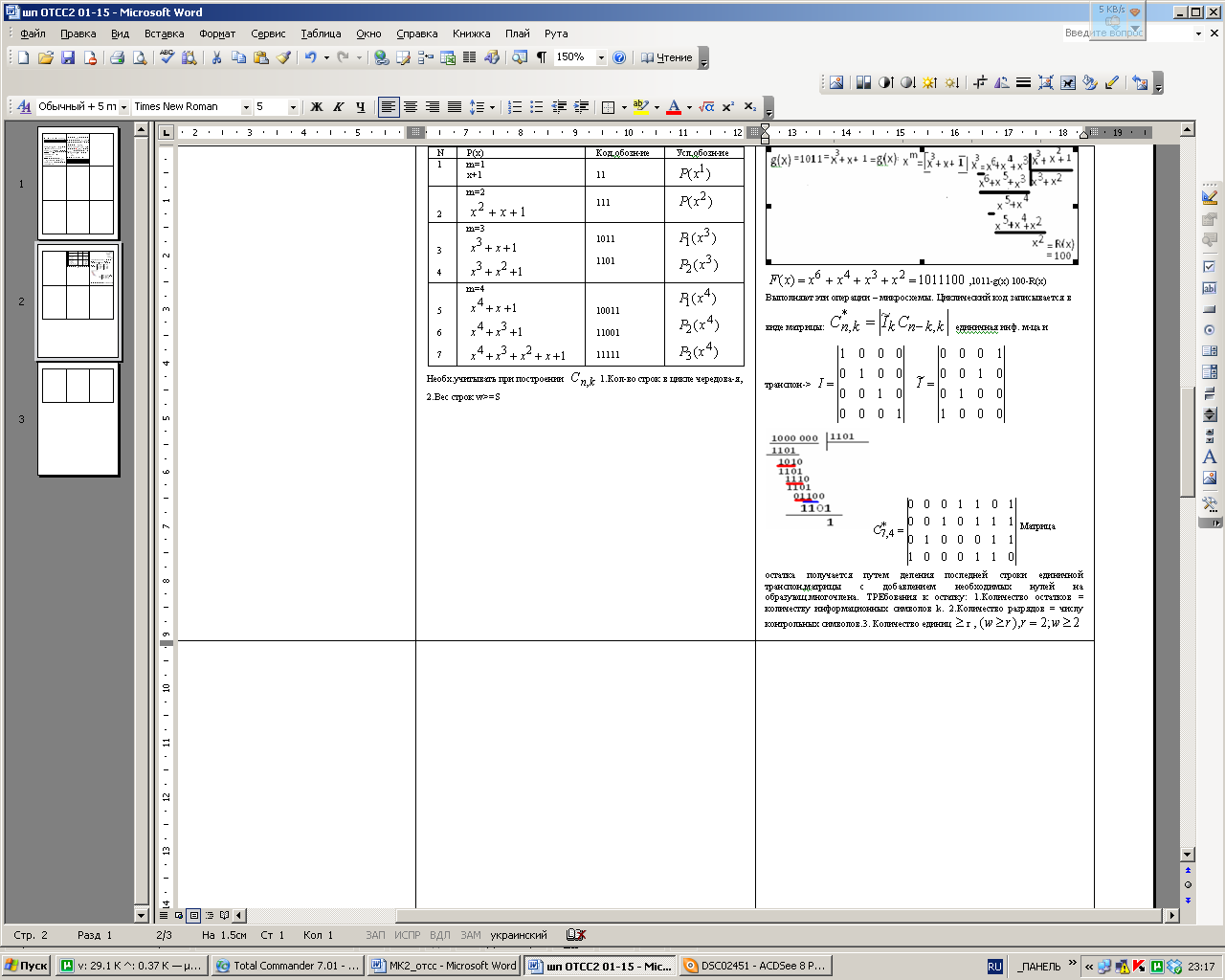
Матрица остатка получается путем деления последней строки единичной транспон.матрицы с добавлением необходимых нулей на образующ.многочлена. ТРЕбования к остатку: 1.Количество остатков = количеству информационных символов k. 2.Количество разрядов = числу контрольных символов.3. Количество единицr ,

33 Понятие образующего многочлена. Требования к выбору образующего полинома многочлена.

Образующий полином P(x) – многочлен фиктивной переменной х, используемый при кодировании ЦК.

P(x) должен удовлетворять условиям:

Если код предназначен для исправления независимых ошибок, то условие – обеспечение заданного кодового расстояния d.

Если код предназначен для исправления пакетов ошибок –обеспечение длины исправляемого(обнаруживаемого) пакета b. 10(0)01(1)1(0)1 b=6

ОП выбирают так, что его степень равна числу проверочных символов m, такжеОП должен входить в разложение двучлена

Доказано каждый двучлен раскладывается на произведение всех без исключения не приводимых двучленов( их степени – делители числа m0):

, напр.=4

Полиномов м.б. несколько. Для любых целых положит.чисел m,S существует циклический код значности. С кодовым расстоянием , при этом число проверочных символов m=n-k не превышает величины .Такой код гарантировано исправляет ошибки кратности S, и ли обнаруживает ошибки кратности2S. Длина пакетов . Число проверочных символов m м.б. определено по оценке границы Варшалова-Гильберта .Определ. с таблицы:

d	k
	1	2	3	4	5	6	7	8	9	10	11
3	2	3	3	3	4	4	4	4	4	4	4
4	2	5	5	6	6	7	7	7	7	8	8
5	4	7	8	8	9	9	10	10	10	11	11
6	5	9	10	11	11	12	12	13	13	14	14

Для различных значений m определены различные степени (неприводимые различные многочлены)