4.2.2 Розв’язання з допомогою рядів Тейлора

Цей метод теоретично годиться для розв’язання будь-яких диференціальних рівнянь, але на практиці не застосовується, оскільки вимагає обчислення частинних похідних, що не тільки незручно, але і почасти неможливо.

Розклад функції в ряд Тейлора в околі точкизаписується у вигляді

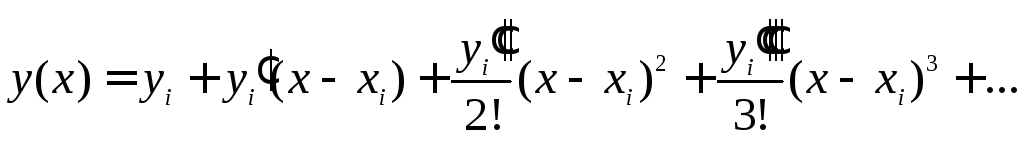(6.4)

Якщо вважати, що знайдені наближені розв’язки рівняння в точках розташованих на деякій відстаніодна від одної, то можна знайти наближений розв’язок для точки , підставивши у формулу (6.4) значення:

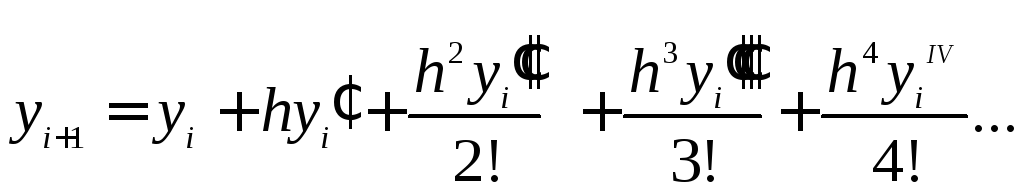. (6.5)

Чим більше членів ряду взято для обчислень, тим точніше буде наближення. З точки зору практичних обчислень метод незручний, оскільки вимагає знаходження різних похідних функції . Проте він надає деякий критерій оцінки різноманітних практично застосовуваних методів – наскільки вони узгоджуються з методом Тейлора. Наприклад, деякі методи узгоджуються до членів порядку, інші – аж до членіві т.д.

6.1.2 Методи Рунге-Кутта

Методи Рунге-Кутта в практиці чисельного розв’язання диференціальних рівнянь застосовуються найбільш часто. Вони володіють такими відрізняючими властивостями:

1) одноступеневі, тобто для знаходження потрібна інформація тільки про попередню точку ();

2) узгоджуються з рядом Тейлора аж до членів порядку , де степіньр різна для різних методів і визначає порядок методу, тобто його точність;

3) не потребує обчислення похідних від .

Відкинемо в (6.5) члени ряду, що містять і т.д., тоді. Оскільки, то отримаємо формулу Ейлера (Рунге-Кутта першого порядку):

. (6.6)

Метод Ейлера (Рунге-Кутта першого порядку) пояснюється рис. 6.1.

Рисунок 6.1 – Геометрична інтерпретація методу Ейлера

На рис.6.1 крива уявляє собою точне, але, звичайно, невідоме рішення рівняння. Припустимо тільки, що нам відоме розташування точки () на цієї кривої. Через дану точку проводими пряму L з тангенсом кута нахилу . Рівняння цієї прямої можна записати у вигляді:

.

Наступною точкою рішення можна вважати ту, в якій пряма перетне пряму L:

,

або

. (6.7)

Формула (6.7), як бачимо, повторює (6.6), тобто є формулою Ейлера. Помилка методу Ейлера зображена на рис.6.1 і зумовлена обмеженням ряду Тейлора (6.5), починаючи з члена другого порядку, тобто:

,

де k – коефіцієнт пропорціональності.

Очевидно, описаний на рис.6.1 процес можна розповсюдити на знаходження і т. д. точок, послідовність яких дасть наближене рішення рівняння. Схема алгоритма рішення диференціального рівняння методом Рунге-Кутта першого порядку наведена на рис. 6.2.

Рисунок 6.2 – Схема алгоритма рішення диференціального рівняння методом Ейлера

Модифікований метод Ейлера (метод Рунге-Кутта другого порядку). Відкинемо в (14.4) члени ряду, що містять і т.д., тоді. (6.8)

Щоб зберегти член ряду, що містить , треба визначити другу похіднуy"(x_i). Її можна апроксимувати розділеною різницею 2-го порядку

Підставляючи цей вираз в ((4.17)), отримаємо

 

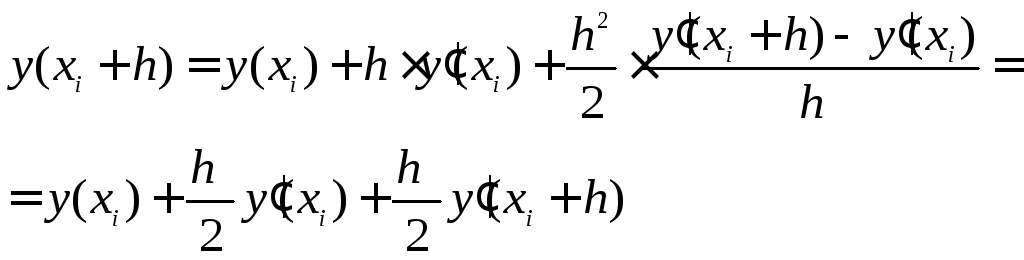
Остаточно, модифікована або уточнена формула Ейлера має вигляд:

. (6.9)

Як видно, для визначення функції y(x) в точці i+1 необхідно знати значення правої частини диференціального рівняння в цій точці, для визначення якої необхідно знати попереднє значення.

Для визначення попереднього значення скористаємося формулою Ейлера. Тоді всі обчислення на кожному кроці за модифікованою або уточненою формулою Ейлера будемо виконувати в два етапи:

На першому етапі обчислюємо попереднє значення за формулою Ейлера

(6.10)

 

На другому етапі уточнюємо значення за модифікованою або уточненою формулою Ейлера

, (6.11)

або

(6.12)

 Остаточно для рішення диференціального рівняння методом Рунге-Кутта другого порядку використовуються формула (6.11) або (6.12). При використанні формули (6.11) алгоритм обчислення чергової точки рішення реалізують в два етапи: спочатку за формулою (6.10) обчислюють прогнозне значення точки , а потім за формулою (6.11) обчислюють остаточне знаближене значення функції в точці. Формула (6.12) дає можливість обчислити значення чергової ординати за один крок.

Точність методу визначається відкинутими членами ряду Тейлора (6.5), тобто .

Розглянемо геометричний зміст модифікованого методу Ейлера (рис.6.3).

 

Рисунок 6.3 – Геометрична інтерпретація методу Рунге-Кутта другого порядку

Оскільки ,, то модифіковану формулу Ейлера можна подати у вигляді

,

де -тангенс кута нахилу дотичної до шуканої функції у(х) в початковій точці кожного кроку, -тангенс кута нахилу дотичної до шуканої функції у(х) в кінцевій точці кожного кроку.

На рисунку 6.3 використані такі позначення:

P₁ - накопичена помилка в (i+1)-й точці за методом Ейлера,

P₂ - накопичена помилка в (i+1)-й точці за модифікованим методом Ейлера.

Як видно з рис.6.3, в першій половині кожного кроку, тобто на ділянці, шукана функціяy(x) апроксимується прямою, яка виходить з точки під кутом, тангенс якого

У другій половині цього ж кроку, тобто на ділянці , шукана функція y(x) апроксимується прямою, яка виходить з точки з координатами під кутом, тангенс якого

У результаті в модифікованому методі Ейлера функція у(х) на кожному кроці апроксимується не однією прямою, а двома.

Схема алгоритма розв’язання диференціального рівняння методом Рунге-Кутта другого порядку наведена на рис. 6.4. В алгоритмі використовуються такі позначення:

права частина конкретного диференціального рівняння ;

початкові умови;

інтервал зміни незалежної величини х;

n – число кроків в розв’язанні;

k – лічильник кількості кроків.

Методи Рунге-Кутта третього і четвертого порядків можна вивести аналогічно методам першого і другого порядків. Але їх графічні інтерпретації не мають такої наглядності, як в попередніх двох випадках, тому наведемо кінцеві співвідношення, що описують дані методи.

Метод Рунге-Кутта третього порядку узгоджується з розкладом в ряд Тейлора аж до членів і описується системою чотирьох співвідношень:

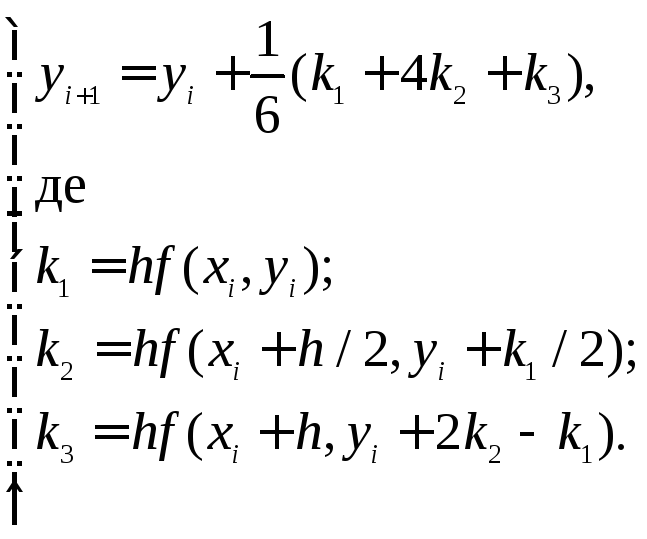(6.13)

Рисунок 6.4 - Схема алгоритма Рунге-Кутта другого порядку

Метод Рунге-Кутта четвертого порядку описується системою п’яти співвідношень:

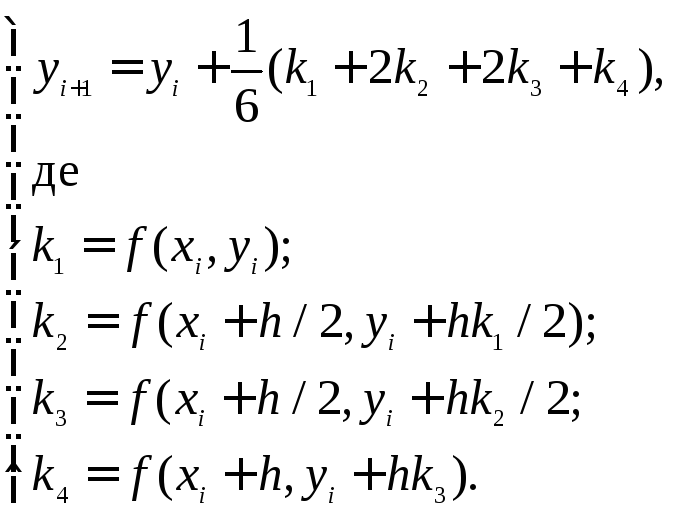(6.14)