7.3. Метод Рунге – Ромберга

Пусть для вычисления величины используется приближенная формула

. (7.3.1)

Здесь  приближенное значение функции , зависящее от некоторого параметраh. И пусть приближенная формула (7.3.1) имеет p-й порядок точности, то есть наблюдается асимптотическое разложение

. (7.3.2)

Введем величину . Заменойполучим из формулы (7.3.2) формулу

. (7.3.3)

При этом учтено, что .

Вычтем из равенства (7.3.2) равенство (7.3.3) почленно:

. (7.3.4)

Здесь учтено, что .

Из формулы (7.3.4) получим

. (7.3.5)

Отсюда получается первую формулу Рунге

. (7.3.6)

При ее выводе учтено, что .

Первая формула Рунге позволяет получить асимптотическую оценку абсолютной погрешности приближенного значения

. (7.3.7)

Эту формулу используют для получения приближенного значения с погрешностью, не превышающей заданного положительного числа. Это делается с использованием метода повторного счета (правила Рунге). Суть его заключается в том, что задается последовательность значений параметраh, которая представляет собой убывающую геометрическую прогрессию

, ,,, … (7.3.8)

Здесь r  некоторое фиксированное число из интервала. Чаще всего значениеr выбирается равным . Очевидно, следовательно,. Далее вычисляются последовательно приближенные значенияприи для каждого значенияn проверяется выполнение неравенства

(7.3.9)

Рано или поздно при достаточно большом значении n это неравенство выполнится и мы получим приближенное значение , которое будет иметь погрешность

,

приближенно не превышающую заданного числа . Следует обратить внимание на то, что для применения метода повторного счета (правила Рунге) достаточно знать только порядок точности приближенной формулыp.

Подставим в лемму (7.3.2) первую формулу Рунге и получим вторую формулу Рунге

. (7.3.10)

Выберем новое приближенное значение по формуле

. (7.3.11)

Из формулы (7.3.10) следует, что

. (7.3.12)

Это означает, что приближенная формула будет иметь порядок точности, больший p. Если асимптотическое разложение (7.3.2) можно продолжить, то есть наблюдается более длинное разложение

, (7.3.13)

то вместо разложения (7.3.12) получим разложение

, (7.3.14)

откуда следует, что новая приближенная формула будет иметь порядок точности, равный .

Итак, вторая формула Рунге позволяет на основе известной приближенной формулы с известным порядком точности получить новую приближенную формулу более высокого порядка точности.

Следует заметить, что формулу (7.3.11) можно применять многократно. Например, на основе полученной приближенной формулы, , имеющей -й порядок точности, можно получить формулус новой правой частью

.

Если асимптотическое разложение (7.3.2) можно продолжать и далее, то новая приближенная формула будет иметь порядок точности, равный.

Пример

Требуется на основе формулы (7.1.14)

,

имеющей первый порядок точности, с помощью метода Рунге–Ромберга получить формулу второго порядка точности.

В

Рис.7.1

ведем пять равноотстоящих узлов:,,,,(рис. 7.1). Расстояние между узламии, а также междуиобозначим черезh. Таким образом, расстояние между соседними узлами равно .

Вычислим вторую производную в точке по формуле (7.1.14) дважды. Первый раз мы используем узлы,,:

.

Выберем и вычислим еще раз вторую производную в точкепо формуле(7.1.14), использовав узлы,,:

.

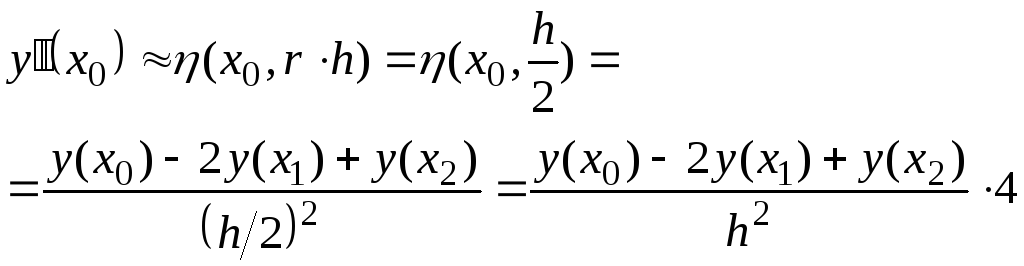А теперь, использовав формулу (7.3.11), получим новую приближенную формулу

В полученной формуле в качестве шага сетки использовано . Поэтому для того чтобы записать полученную формулу при стандартном обозначении шага сетки (h), сделаем замену :

. (7.3.15)

Формула (7.3.15) имеет второй порядок точности. Эту формулу можно обобщить, если в качестве узлов ,,,,использовать,,,,:

. (7.3.16)