Задача № 8

Изобразить на чертеже области, задаваемые системой неравенств.

№ п/п	Система неравенств	№ п/п	Система неравенств
1		16
2		17
3		18
4		19
5		20
6		21
7		22
№ п/п	Система неравенств	№ п/п	Система неравенств
8		23
9		24
10		25
11		26
12		27
13		28
14		29
15		30

Задача № 9

Привести к каноническому виду уравнение поверхности второго порядка с помощью теории квадратичных форм. Сделать чертеж поверхности в канонической системе координат.

Вариант	Уравнение	Вариант	Уравнение
1	х2+4ху+у2+z2=0	16	2х2+4у2+2z2+2xz-12=0
2	х2+4ху+у2+2z2-6=0	17	2х2-3у2+2z2+2xz=0
3	х2+4ху+у2-2z2=0	18	2х2-3у2+2z2-2xz-12=0
4	х2+4ху+у2-3z2+12=0	19	2х2-3у2+2z2-6xz+36=0
5	2х2-6ху+2у2+z2=0	20	2х2+2у2+2z2+2yz-1=0
6	2х2-6ху+2у2+2z2-25=0	21	2х2-2у2-2yz -2z2+1=0
7	3х2+4ху+3у2+2z2-50=0	22	2х2-2у2-6yz- 2z2-1=0
8	3х2+4ху+3у2-2z2=0	23	х2-у2-yz-z2=0
9	3х2+4ху+3у2-z2-100=0	24	х2-3у2-2yz-3z2-1=0
10	2хz-3y2=0	25	х2+3у2+2yz+3z2+1=0
Вариант	Уравнение	Вариант	Уравнение
11	х2+4ху+у2-4z2-12=0	26	3х2-3у2-2yz-3z2=0
12	2ху-3z2=0	27	2х2-3у2-2yz-3z2-1=0
13	х2+4хz+5у2+z2=0	28	х2+2у2+6yz+2z2+10=0
14	3x2-2yz=0	29	3х2+2у2-6yz+2z2-10=0
15	х2+6хz+5у2+z2-15=0	30	х2+у2-6yz+z2=0

Указания к выполнению и примеры решения задач расчетно-графической работы

Задача 1

Чтобы найти длины диагоналей параллелограмма и острый угол между ними, необходимо выразить диагонали параллелограмма через векторы ииспользуя операции над векторами.

Чтобы решить задачу, потребуются формулы:

–длина вектора,

–острый угол между векторами ,

S_парал.=– площадь параллелограмма, построенного на векторах.

Задача 2

Чтобы решить задачу, потребуются формулы:

1. А(х₁,у₁,z₁), В(х₂,у₂,z₂), – координаты вектора;

2. ; – длина вектора;

3. , ;

- острый угол между векторами ;

4. S_=– площадь треугольника, построенного на векторах;

5. V_пир-да=– объем пирамиды, построенной на векторах,;.

Задача 3

Рассмотрим примеры решения задач.

Построить кривую , заданную уравнением в полярной системе координат.

Решение. Составим таблицу значений функции

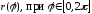с шагом .

;

;

;

;

;

;

;

;

;

;

;

;

;

;

;

.

Таким образом, получим таблицу значений функции .

Таблица 1

	0
r	3	5,1	6	5,1	3	0,9	0	0,9	3	5,1	6	5,1	3	0,9	0	0,9	3

Построим заданную кривую.

Задача 4

Решить графически систему линейных неравенств

Решение

1. Построим прямые (рис.1):

1. ; 2) ; 3).

х1	0	2		х1	0	2		х1	0	-3
х2	6	0		х2	1	0		х2	2	0

2. Для каждой прямой определим полуплоскость, которая задается неравенством. Для этого возьмем произвольную точку, не лежащую на прямой, и подставим ее координаты в неравенство. Если неравенство будет верным, то полуплоскость, содержащая выбранную точку, и является решением исходного неравенства. Если неравенство будет неверным, то решением неравенства будет полуплоскость по другую сторону прямой.

1. Возьмем, например, точку О(0;0): 30+06 (верно), значит решением неравенства будет полуплоскость, содержащая эту точку.

2. Возьмем точку О(0;0) и подставим ее координаты во второе неравенство: 0+01 (неверно). Значит, решением неравенства является полуплоскость, не содержащая точку О.

3. Выберем, например, точку О(0;0) и подставим ее координаты в третье неравенство: -20+306 (верно). Значит, решением неравенства является полуплоскость, содержащая точку О.

3. Решением системы неравенств будет область пересечения всех полуплоскостей, являющихся решением каждого из неравенств системы. В данном примере решением системы является область АВСDEFG. Так как по условию х₁>0 и x₂>0, то области АВС и EFG исключаются из решения. Таким образом, получаем область АСDEG, в которой координаты всех точек, кроме D известны. Найдем координаты точки D. Необходимо решить систему уравнений:

ее решением будет т..

Ответ: АСDEG – область решений системы.

Задача 5

Будьте внимательны: условия примера не совпадают с условиями задания!

Даны координаты вершин треугольника :,,. Найти: 1) длину стороны; 2) уравнения сторонии их угловые коэффициенты; 3) внутренний уголв радианах с точностью до; 4) уравнение высотыи ее длину, не используя координаты точки; 5) уравнение медианы; 6) точку пересечения высот треугольника. Сделать чертеж.

Решение: Сделаем чертеж (рис.3).

Рис. 3

1. Расстояние между точками инаходится по формуле.

В данном случае .

2. Уравнение прямой, проходящей через две заданные точки плоскости иимеет вид.

Следовательно, для прямой имеем– общее уравнение прямой.

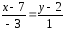
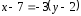
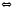
Аналогично, для прямой имеем– общее уравнение прямой.

Найдем угловые коэффициенты прямых и. Для этого перейдем от общего уравнения прямой к уравнению прямой с угловым коэффициентом.

Для прямой имеем, то есть– угловой коэффициент прямой. Для прямой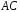получим, значит– угловой коэффициент прямой.

3. Учитывая, что угол острый, воспользуемся формулой.

Имеем , откуда

4. Для нахождения уравнения высоты воспользуемся формулой уравнения прямой, проходящей через данную точкус заданным угловым коэффициентом:.

В данном случае ;(координаты точки). Так как прямыеиперпендикулярны, то их угловые коэффициенты связаны соотношением, откуда. Значит, уравнение высотыбудет иметь вид:или.

Для нахождения длины высоты воспользуемся формулой расстоянияот заданной точкидо прямой: .

В данном случае ,(координаты точки);;;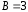(коэффициенты из общего уравнения прямой). Следовательно,.

5. Уравнение медианы составим, используя уравнение прямой, проходящей через две заданные точки.

Так как – медиана, то координаты точкинайдем как координаты середины отрезка:;, то есть. Тогда уравнение медианыбудет иметь вид:или.

6. Для нахождения координат точки пересечения высот треугольниканайдем уравнение высоты.

Уравнение высоты находим по формуле. По условию,. Так как прямыеиперпендикулярны, то;. Значит, уравнение высотыбудет иметь видили.

Составляем и решаем систему уравнений: Значит,.

Задача 6

Для нахождения канонических уравнений прямых А₁А₂ и А₁А₄ могут быть использованы формулы:

- уравнение прямой по двум точкам (х₁,y_1, z₁) и (х₂,y_2,z₂);

- каноническое уравнение прямой, где

(х₀,y_0, z₀) – координаты точки, принадлежащей прямой, {m,n,p} – координаты направляющего вектора прямой.

Для нахождения угла между прямыми следует воспользоваться формулой:

, где – направляющие векторы прямых.

Для составления уравнения плоскости можно пользоваться формулами:

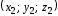, где ,,- координаты точек, принадлежащих плоскости, или А()+В()+С()=0, где- координаты точки, принадлежащей плоскости, {A,B,C} – координаты вектора нормали для плоскости.

Угол между прямой и плоскостью находится по формуле:

,

где – направляющий вектор прямой,{A,B,C} – вектор нормали к плоскости.

Для составления уравнения высоты, опущенной из вершины А₄ на грань А₁А₂А₃ следует воспользоваться условием перпендикулярности прямой и плоскости: || и каноническим уравнением прямой.

Для нахождения расстояния от точки А₄ до грани А₁А₂А₃ следует воспользоваться формулой:

где Ах+Ву+Сz+D=0 – уравнение плоскости; - координаты точки.

Задача 7

Найти координаты точки М₁, симметричной точке М(5;-2;-1) относительно плоскости : 4х+10у-8z-53=0 и точки М₂, симметричной точке М относительно прямой l:

Решение. Найдем точку М₁. Эта точка симметрична точки М относительно заданной плоскости , лежит на прямой М₁М перпендикулярной плоскости . При этом точка пересечения прямой М₁М и плоскости  (обозначим ее О) делит отрезок М₁М пополам (рис.4)

М

О



М₁

Рис.4

Составим уравнение прямой М₁М. Поскольку прямая М₁М перпендикулярна плоскости , то вектор нормали плоскости  будет являться направляющим вектором прямой М₁М, т.е. Воспользуемся каноническим уравнением прямой, где (х₀,у₀,z₀) – координаты точки, принадлежащей прямой, {m,n,p} – координаты направляющего вектора прямой. В нашем случае (х₀,у₀,z₀) – это координаты точки М; {m,n,p}={4;10;-8}. Значит уравнение прямой М₁М имеет вид:

Запишем уравнение прямой М₁М в параметрическом виде

Найдем координаты точки О – точки пересечения прямой М₁М и плоскости . Для этого решим систему уравнений:

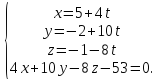
Подставляя x,y,z из первых трех уравнений в четвертое, получим

4(5+4t)+10(-2+10t)-8(-1-8t)-53=0 или 180t-45=0, откуда t=1/4.

Определим координаты точки О:

х=5+4(1/4)=6; у=-2+10(1/4)=1/2; z=-1-8(1/4)=-3.

О(6;1/2;-3).

Найдем координаты точки М₁, воспользовавшись формулами деления отрезка пополам. В нашем случае О – это середина отрезка М₁М, поэтому эти формулы запишутся в виде

Следовательно, М₁(7;3;-5).

Найдем координаты точки М₂. Эта точка симметричная точке М относительно заданной прямой l, лежит на прямой М₂М, перпендикулярной прямой l. При этом точка пересечения прямых О делит отрезок М₂М пополам (рис.5).



М

l

О

М₂

Рис.5

Составим уравнение плоскости , проходящей через точку М, перпендикулярно заданной прямой l. Поскольку прямая l перпендикулярна плоскости , то направляющий вектор прямой l будет являться вектором нормали для плоскости . Поэтому можно воспользоваться формулой А(х-х₀)+В(у-у₀)+С(z-z₀)=0, где (х₀,у₀,z₀) – координаты точки, принадлежащей плоскости, {А,В,С} – координаты вектора нормали плоскости. В нашем случае (х₀,у₀,z₀) – это координаты точки М, а {А,В,С}=. Следовательно,

2(х-5)-1(у+2)+2(z+1)=0 или 2х-у+2z-10=0 – уравнение плоскости , содержащей прямую ММ₂.

Запишем уравнение заданной прямой l в параметрическом виде

Найдем координаты точки О – точки пересечения заданной прямой l и плоскости . Для этого решим систему уравнений

Подставим x,y,z из первых трех уравнений в четвертое, получим

2(5+2t)-(1-t)+2(-4+2t)-10=0 или 9t-9=0, откуда t=1. Определим координаты точки О: х=5+21=7; у=1-1=0; z=-4+21=-2. Следовательно, О(7;0;-2). Найдем координаты точки М₂, воспользовавшись формулами деления отрезка пополам. В нашем случае О – середина отрезка ММ₂, поэтому эти формулы запишутся в виде:

Следовательно, М₂(9;2;-3).

Задача 8

Изобразить на чертеже области, задаваемые системой неравенств .

Решим графически первое неравенство, для этого необходимо построить график функции, заданной в неравенстве, и определить область, которая соответствует неравенству.

Приведем уравнение кривой, заданной в неравенстве, к каноническому виду, а затем построим ее.

1. Определим угол поворота осей координат. Для этого используются формулы:

где А и С коэффициенты при х² и у² соответственно, 2В – коэффициент при ху.

В нашем случае А=2; 2В=-2, С=2, тогда Отсюда, следовательно,).

2. Используя формулы преобразования координат, выразим старые переменные через новые.

x=x'cos-y'sin=x'cos45-y'sin45=(x'-y');

у=x'sin+y'cos- =x'sin45+y'co 45=(x'+y').

Полученные выражения для х и у подготовим в уравнение кривой.

2((x'-y'))²-2(x'-y')(x'+y')+2((x'-y'))²+6(x'-y')- 6(x'+y')-6=0.

После преобразования получаем x'²+3y'²-6y'-6=0.

3. Выполним параллельный перенос системы координат. Для этого выделим полный квадрат, в данном случае, по переменной у, чтобы определить новый центр координат.

x'²+3(y'²-2y'+²)- 3² -6=0,

x'²+3(y'-) ²=12.

Сделаем замену переменных:

х"=x'

y"=y'-. Следовательно, О'(0;) – новый центр координат.

Замечание 1

После подстановки выражений для х и у в уравнение кривой могут получиться уравнения вида

1. ax'²+bx'+cy'²+dy'+f=0. В этом случае полные квадраты следует выделять по переменным x' и y';

2. ax'²+dy'+f=0 или cy'²+bx'+f=0. В этом случае уравнения следует записывать в виде

ax'²+d(y'+)=0 илису'²+b(x'+)=0 и сделать замену переменных следующим образом:

x"=x' или x"=x'+;

y"=y'+y"=y';

3. ax'²+bx'+dy'+f=0 или cy'²+dy'+bx'+ f=0. В этом случае сначала необходимо выделить полные квадраты (в первом уравнении по переменной х', во втором – по у'), потом линейную часть уравнения представить так, как описано в пункте 2 этого замечания, а затем ввести замену переменных.

Таким образом, получим

x"²+3y"²=12 или – уравнение эллипса.

1. Построим систему координат Оху (рис.2).

2. Построим систему координат Ох'y'. Для этого повернем оси на угол =45 против часовой стрелки.

3. В системе координат Ох'y' отметим точку О'(0;).

4. Построим систему координат О'x"y". Для этого через точку О' параллельно осям х' и y' проведем оси х" и y".

5. В системе координат О'x"y" построим эллипс .

6. Определяем область решения первого неравенства. Построенный эллипс разбил плоскость на две области: внутреннюю и внешнюю. В системе координат Оху выберем произвольную точку, не лежащую на кривой, например, т.О(0;0) и подставим ее координаты в исходное равенство. 20²-200+20²+60-60-60, -60 – верно.

Значит, множеством решений первого неравенства будет область, которой принадлежит выбранная точка О, т.е. внутренняя часть эллипса.

Замечание 2

Если бы после подстановки выбранной точки в исходное неравенство получилось бы неверное числовое неравенство, то множеством решений неравенства являлась бы область, которой выбранная точка не принадлежит.

Решим графически второе неравенство. Для этого построим прямую 2х+у=2.

х	0	1
у	2	0

Определяем область решения второго неравенства. Построенная прямая разбила плоскость на две области: верхнюю и нижнюю. В системе координат Оху выберем произвольную точку, не лежащую на кривой, например, т.О(0;0) и подставим ее координаты в исходное равенство. 20+02, 02 – неверно.

Значит, множеством решений второго неравенства будет область, которой не принадлежит выбранная точка О, т.е. верхняя полуплоскость.

Таким образом, исходная система неравенств, задает область, изображенную на рис. 5.

Задача 9

Привести к каноническому виду уравнение поверхности второго порядка 3х²+3у²-2yz+3z²-1=0 с помощью теории квадратичных форм. Сделать чертеж поверхности в канонической системе координат.

Решение. Поскольку для квадратичной формы а₁₁х²+а₂₂у²+а₃₃z²+2a₁₂xy+2a₁₃xz+2a₂₃yz матрица имеет вид

то в нашем примере матрица старших членов уравнения поверхности имеет вид

Найдем собственные значения этой матрицы. Для этого составим и решим характеристическое уравнение

которое приводится к виду (3-)³-(3-)=0 или (3-)(²-6+8)=0. Отсюда находим ₁=3, ₂=2, ₃=4. Найдем собственные векторы для каждого собственного значения.

Пусть – собственный вектор. Координаты собственных векторов являются решениями системы (А-Е). В нашем случае эта система имеет вид

При ₁=3 получаем систему

Следовательно, в системе 2 главные неизвестные, 1 свободная. Пусть х₁- свободная неизвестная, придадим ей значение 1, т.е. х₁=1. Тогда получаем собственный вектор для собственного значения₁=3.

При ₂=2 получаем систему

Следовательно, в системе две главные неизвестные, одна свободная. Пусть х₃ – свободная неизвестная, придадим ей значение 1, т.е. х₃=1. Тогда получаем систему

Значит, собственный вектор для собственного значения₂=2.

При ₃=4 получаем систему

Следовательно, в системе две главные неизвестные, одна свободная. Пусть х₃ – свободная неизвестная, придадим ей значение 1, т.е. х₃=1. Тогда получаем систему

Значит, собственный вектор для собственного значения₃=4.

Пронормируем собственные векторы.

следовательно,

следовательно,

следовательно,

Запишем матрицу преобразования координат

Отсюда получаем формулы преобразования координат x=x'; y=y'-z'

z=

Значения х,у,z подставим в исходное уравнение поверхности

или 3x'²+2y'²+4z'²-1=0.

Заметим, что коэффициенты x'², у'², z'², как и должно было быть, являются соответственно собственными значениями ₁, ₂, ₃.

Таким образом, получили уравнение поверхности 3x'²+2y'²+4z'²=1 или эллипсоид (рис.8).

Рис. 8