1.4. Третий канал возмущения

- построение переходной функции

Так как запаздывание только сдвигает переходную функцию на время t, то вывод переходной функции будем делать для аналогичного звена без запаздывания, а «t» - учтем в окончательной формуле. Таким образом, передаточная функция объекта имеет вид:

W_в3(p)=W_в3⁰(p)×е^-pt

Х_вх(t)=1(t)– входной сигнал.

Изображение выходного сигнала имеет вид:

Рассмотрим характеристическое уравнение .

Найдем дискриминант: D = b₁² - 4×b₂ = 75² - 4×2500 =-4375

Следовательно, корни характеристического уравнения комплексные и имеют вид:

,обозначимp₁ = p₂ = a ± jw .

Определяем коэффициенты А, В, С:

A×p²×b₂ + A×b₁×p+A+B×p² + C×p = K×p×a + K

при р²: A×b₂ + B =0

при р¹: A×b₁ + C = K×a

при р⁰: A = K

A =K

B =-K× b₂

C = K× (a - b₁)

Находим оригинал:

Учтем явление транспортного запаздывания, то есть при t³tпереходная функция имеет вид:

(1.27)

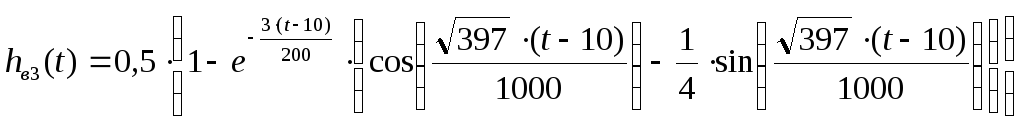
(1.28)

При t<th(t) = 0.

Расчетные данные для построения переходного процесса:

t	0	10	40	70	100	130	160	190	220	250	280
h(t)	0	0	0,281	0,473	0,560	0,575	0,554	0,527	0,506	0,496	0,493

t	310	340	370	400	430	460	490	520	550	580	610
h(t)	0,494	0,497	0,499	0,500	0,501	0,501	0,500	0,500	0,500	0,500	0,500

Рис.1.23 Переходная функция по каналу возмущения 3.

Переходный процесс объекта по каналу возмущения 3 имеет запаздывание =10. Так как передаточная функция объекта по каналу регулирования имеет в свеем составе передаточную функцию колебательного звена, то переходный процесс объекта по каналу регулирования имеет колебательный характер и по окончании переходного процесса выходная величина выходит на установившееся значение К=0,5.

- построение амплитудно-частотной характеристики

(1.29)

(1.30)

Определяем резонансную частоту:

Расчетные данные для построения АЧХ:

w	0	0,01	0,02	0,0287	0,03	0,04	0,05	0,06	0,07	0,08	0,09	0,1
А(w)	0,50	0,56	0,69	0,74	0,74	0,67	0,57	0,48	0,41	0,36	0,32	0,29

w	0,11	0,12	0,13	0,14	0,15	0,16	0,17	0,18	0,19	0,2	0,21
А(w)	0,26	0,24	0,22	0,20	0,19	0,18	0,17	0,16	0,15	0,14	0,13

Рис. 1.24 Амплитудно-частотная характеристика по каналу возмущения 3.

Так как объект по каналу возмущения 3 имеет колебательную составляющую, то по этому каналу объект является фильтром низких частот и при этом если частота гармонического входного сигнала близка к частоте собственных колебаний звена , то отношение амплитуды выходного сигнала к амплитуде входного больше передаточного коэффициента К=0,5 (т.е. наблюдается резонанс).

- построение фазо-частотной характеристики

При w = Ö1/b₂ = Ö1/900 = 0,033 и

Следовательно, при w ≤ 0,033

(1.31)

, (1.32)

а при w>0,033

(1.33)

(1.34)

Расчетные данные для построения ФЧХ:

w	0,05	0,055	0,06	0,065	0,07	0,075	0,08	0,085	0,09	0,095	0,01	0,105
j(w)	-1,91	-1,98	-2,04	-2,11	-2,17	-2,22	-2,28	-2,34	-2,39	-2,45	-2,50	-2,55

w	0	0,005	0,01	0,015	0,017	0,02	0,025	0,03	0,035	0,04	0,045
j(w)	0,00	0,10	-0,07	-0,53	-0,71	-1,02	-1,33	-1,52	-1,65	-1,75	-1,83

Рис.1.25 Фазо-частотная характеристика по каналу возмущения 3

В режиме гармонических колебаний присутствуют отрицательные фазовые сдвиги из-за составляющей колебательного звена и звена транспортного запаздывания. А так как еще есть и составляющая пропорционально-дифференциального звена, то могут быть положительные фазовые сдвиги, но они не проявились из-за того, что коэффициенты пропорционально-дифференциального звена небольшие, т.е. его влияние слабее влияния колебательного звена и звена транспортного запаздывания.

-построение амплитудно-фазовой характеристики

(1.35)

(1.36)

Расчетные данные для построения АФХ:

w	0	0,01	0,02	0,03	0,04	0,05	0,06	0,07	0,08	0,09	0,1
Re(w)	0,50	0,56	0,66	0,55	0,29	0,07	-0,05	-0,12	-0,16	-0,18	-0,19
Im(w)	0,00	-0,12	-0,89	-2,12	-2,65	-2,51	-2,18	-1,85	-1,58	-1,35	-1,16

w	0,15	0,2	0,25	0,3	0,4	0,5	0,6	0,7	0,8	0,9	1
Re(w)	-0,18	-0,13	-0,08	-0,02	0,05	0,05	0,01	-0,03	-0,03	-0,01	0,01
Im(w)	-0,54	-0,21	-0,02	0,07	0,10	0,03	-0,04	-0,05	-0,01	0,02	0,03

Рис.1.26 Амплитудно-фазовая характеристика по каналу возмущения 3