
DM_1 / Деталі машин КЛ [Стадник В. А
.].pdf
|
|
|
|
|
|
|
he |
= hae + h fe = 2 ,2me ; |
|
|
|
|
|
|||||||||||||||||||||||
радіальний зазор |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
C = C* me |
= 0 ,2me . |
|
|
|
|
|
|
|
|
||||||||||||||||||
Розміри вінців конічних шестірні та колеса: |
|
|
|
|
||||||||||||||||||||||||||||||||
зовнішні ділильні діаметри |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
d |
e1 |
= m |
e |
Z |
1 |
; d |
|
|
= m |
e |
Z |
2 |
; |
|
|
|
(10.35) |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e2 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
зовнішні діаметри вершин зубців |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
dae1 |
= de1 |
|
+ 2hae cos δ 1 = de1 |
|
+ 2me cos δ 1 ; |
(10.36) |
||||||||||||||||||||||||||||||
dae 2 |
= de 2 |
+ 2hae cos δ |
|
|
= de 2 + |
2me cos δ 2 ; |
||||||||||||||||||||||||||||||
2 |
|
|
||||||||||||||||||||||||||||||||||
зовнішні діаметри западин |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
d fe1 |
= de1 |
− 2h fe cos δ 1 |
= de1 |
− 2 ,4me cos δ 1 ; |
(10.37) |
|||||||||||||||||||||||||||||||
d fe1 |
= de 2 |
− 2h fe cos δ 2 = de2 |
− 2 ,4me cos δ |
2 ; |
||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||
зовнішня конусна відстань |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
d |
|
|
|
|
2 |
d |
|
|
|
2 |
|
|
|
m |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
e 1 |
|
e 2 |
|
|
|
|
e |
|
|
|
|
|
|
2 |
|
2 |
|
|
|||||||||||||||
Re |
= |
|
|
|
|
|
|
+ |
|
|
|
|
|
= |
|
|
|
|
|
|
|
Z1 |
+ |
Z 2 |
; |
(10.38) |
||||||||||
|
2 |
|
|
|
2 |
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
коефіцієнт ширини |
|
зубчастого |
|
вінця |
|
|
|
ψ |
|
|
|
= b |
= 0,2…0,30; ширина |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
bRe |
|
Re |
|
|
||||||||||||||||||||||||
зубчастого вінця b =ψ bRe × Re , але за умови, що b ≤10 me ; |
|
|||||||||||||||||||||||||||||||||||
середня конусна відстань |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
Rm = Rb − 0 ,5b ; |
|
|
|
|
|
|
|
|
(10.39) |
|||||||||||||||||
середній коловий модуль зубців |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
mm = |
me Rm |
Re |
; |
|
|
|
|
|
|
|
|
|
|
(10.40) |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
середні ділильні діаметри шестірні та колеса |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
dm1 |
|
= mm Z1 ; |
|
|
|
|
|
|
dm 2 |
|
= mm Z2 ; |
|
|
(10.41) |
||||||||||||||||||||
кути головки θa та ніжки θ f |
зубця |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
220 |
|
|
|
|
|
|
|
|
|||||

tgθa |
h |
|
|
; tgθ f = |
hfe |
|
; |
(10.42) |
|||||
= |
ae |
|
|
Re |
|||||||||
|
|
|
|
Re |
|
|
|
|
|
|
|||
кути конуса вершин зубців шестірні та колеса |
|
|
|
||||||||||
δ |
a1 |
= δ |
1 |
+ θ |
a |
; δ |
a |
= δ |
2 |
+ θ |
a |
; |
(10.43) |
|
|
|
|
2 |
|
|
|
||||||
кути конуса западин шестірні та колеса |
|
|
|
|
|
||||||||
δ |
f 1 |
= δ |
1 |
− θ |
f |
; δ |
f |
= δ |
2 |
− θ |
f |
. |
(10.44) |
|
|
|
|
1 |
|
|
|
||||||
Передатне число. Кути ділильних (початкових) конусів δ 1 |
і δ 2 зв'язані |
||||||||||||
з передатним числом так же, як і в конічних фрикційних передачах. Аналогічно конічній фрикційній передачі при Σ =90˚ передатне число
u = ω1 ω2 = n1 n2 = de2 |
|
de1 |
= tgδ 2 = ctgδ 1 |
(10.45) |
||||||
звідки |
δ |
1 |
= arcctgδ |
1 |
і |
δ |
2 |
= arctgδ |
2 . |
(10.46) |
|
|
|
|
|
||||||
Для конічної прямозубої передачі рекомендується u =2; 2,5; 3,15; 4.
Додаткові співвідношення між розмірами елементів конічної
зубчастої передачі, які будуть використані у подальших теоретичних викладках:
передатне число конічної зубчастої передачі
|
u = ω1 ω2 |
= de 2 de1 |
= dm 2 dm1 |
= Z2 |
Z1 |
; |
|
|
|
(10.47) |
|||||||||||||||||||
кути при вершинах початкових конусів шестірні та колеса |
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
tgδ |
= 1 |
u |
; tgδ |
2 |
= u ; |
|
|
|
|
|
|
|
|
|
(10.48) |
|||||||||
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
зовнішня конусна відстань |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d |
|
|
|
2 |
d |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Re |
= |
|
|
|
|
|
|
|
= 0 ,5de1 |
|
1 + u |
2 |
|
; |
(10.49) |
||||||||||||||
|
|
e1 |
|
|
+ |
e 2 |
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
2 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
ділильні діаметри, виражені через R та u , |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
d |
e1 |
= |
2 Re |
|
|
|
|
; |
d |
e2 |
= |
|
2 Re u |
|
|
|
|
; |
|
|
(10.50) |
||||||||
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
1 + u2 |
|
|
|
|
|
|
|
+ u2 |
|
|
|
|
|||||||||||
221
dm1 = |
2 Rm |
; dm 2 |
= |
2 Rm u |
; |
||
|
1 + u2 |
|
1 + u2 |
||||
середня конусна відстань, середній коловий модуль та середні ділильні діаметри
Rm
mm
dm1
= Re |
− 0 ,5b = Re (1 − 0 ,5ψ bRe ); |
|
||
= me |
(1 − 0 ,5ψ bRe |
); |
(1 − 0 ,5ψ bRe |
(10.51) |
= de1 (1 − 0 ,5ψ bRe |
); dm2 = de2 |
). |
||
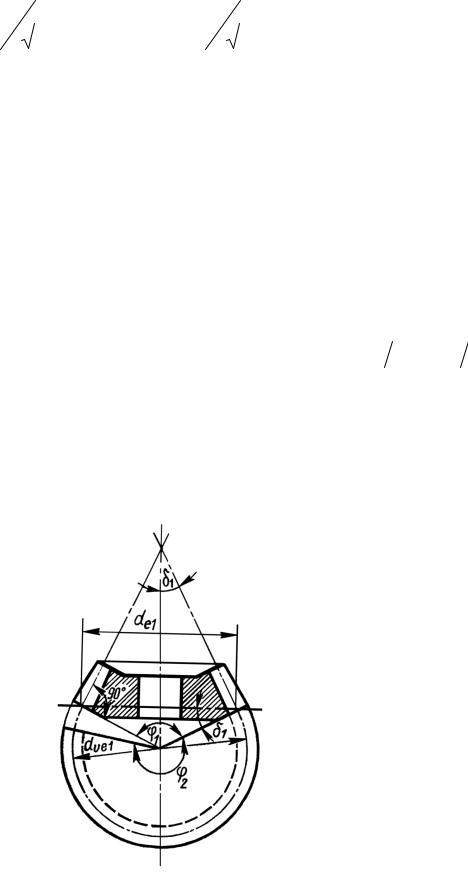
Зведення прямозубого конічного колеса до еквівалентного прямозубого
|
циліндричного колеса. |
|
Дійсні |
профілі зубців конічних коліс дуже близькі |
до профілів |
циліндричних прямозубих коліс, початкові (ділильні) радіуси de1 |
2 і de2 2 |
|
(рис. 10.9) яких рівні довжинам твірних додаткових конусів. Такі циліндричні прямозубі колеса називають еквівалентними. Еквівалентне циліндричне колесо одержуємо як розгортку додаткового конуса, яка обмежена кутом ϕ2 (рис. 10.11)
Рис. 10.11. До визначення еквівалентного числа зубців
ZV конічного колеса
222
Діаметри еквівалентних коліс
d |
|
= |
de |
1 |
= |
|
m |
e |
Z |
1 |
|
= m |
|
Z |
; |
|||
1 |
|
|
|
|
|
|
|
|
|
|||||||||
Ve |
|
cos |
δ1 |
|
|
cos δ1 |
|
e V1 |
|
|||||||||
|
|
|
|
|
|
|
|
(10.52) |
||||||||||
|
|
|
de |
|
|
|
|
m |
|
Z |
|
|
|
|
|
|||
d |
|
= |
2 |
|
= |
|
e |
2 |
|
= m |
Z |
, |
||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|||||||
Ve |
|
cos |
δ2 |
|
|
|
cosδ2 |
|
|
e V2 |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|||||||||
звідки еквівалентне число зубців |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
ZV1 |
= |
Z1 |
|
; ZV2 = |
Z2 |
|
. |
(10.53) |
|
cosδ |
1 |
cos δ |
2 |
||||||
|
|
|
|
|
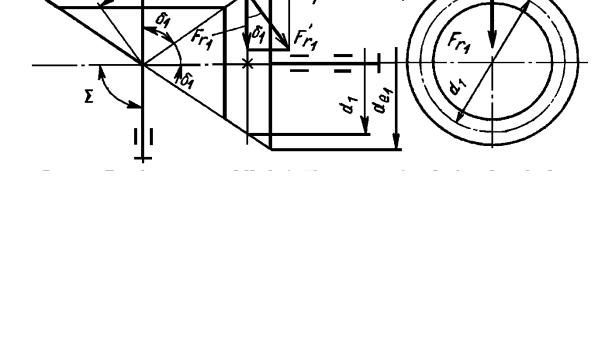
Сили в зачепленні прямозубої конічної передачі.
Сили в зачепленні (рис. 10.12) визначають за розмірами в середньому перерізі зуба шестірні.
Рис. 10.12. Сили в зачепленні прямозубої конічної передачі.
Сила Fn1 діє перпендикулярно поверхні зуба під кутом α до твірної ділильного конуса. Спочатку її розкладають на дві сили Ft1 і Fr1 ′. В свою чергу сила Fr1 ′ = Ft1 × tgα розкладається на дві сили Fr1 і Fa1 . Таким чином,
на шестірню конічної прямозубої передачі діють три сили:
223
колова |
|
|
|
|
|
|
|
|
|
|
F |
= |
2T1 |
; |
|
(10.54) |
|
|
|
|
|
|||||
|
|
t1 |
|
d1 |
|
|
|
|
|
|
|
|
|
|
|
||
радіальна |
|
|
|
|
|
|
|
|
Fr |
= Fr′ cos δ1 |
= Ft |
1 |
× tgα × cosδ1 ; |
(10.55) |
|||
1 |
|
|
|
|
|
|
|
|
осьова |
|
|
|
|
|
|
|
|
Fa1 |
= Fr′ sinδ1 = Ft1 |
× tgα × sinδ1 . |
(10.56) |
|||||
Для колеса напрям сил протилежний, при цьому: |
|
|||||||
F |
= F ; |
F |
= F |
|
; F |
= F . |
(10.57) |
|
t 2 |
t1 |
r2 |
|
a1 |
a2 |
r1 |
|
|
Визначення розрахункового навантаження при розрахунку
на згин і контактну міцність зубців
прямозубих конічних передач
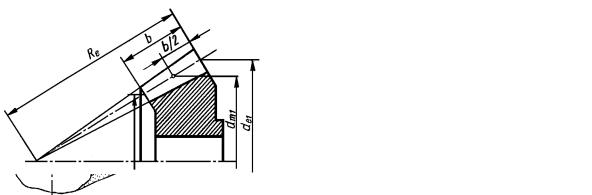
Площі поперечних перерізів, модуль зубців конічного зубчастого колеса і величина питомого навантаження q на зуб пропорціональні відстаням від
вершини початкового (ділильного) конуса. Навантаження розподіляється за законом трикутника від qmin до qmax (рис. 10.13. б), вершина якого співпадає з вершиною початкового (ділильного) конусу (рис. 10.13 а), а тому напруження
згину однакові по всій довжині зуба. |
|
a) |
б) |
Рис. 10.13. Розподіл навантаження по довжині зуба в конічній прямозубій передачі: а – осьовий переріз зуба; б – схема розподілу питомого навантаження q .
224

А тому розрахунок на згин можна виконувати за будь-яким перерізом. На практиці за розрахунковий переріз прийнято середній переріз зуба з ділильним діаметром dm , для якого розрахункове навантаження у розрахунках на згин
визначиться за формулою
F |
= F × K |
F |
= |
2T2 × K Fβ × K FV |
, |
(10.58) |
|
|
|||||||
t p |
t |
|
dm2 |
|
|||
|
|
|
|
|
|
||
де K F = K Fβ × K FV - коефіцієнт навантаження. |
|
||||||
Коефіцієнт |
K Fβ |
- приймають за графіком (рис. 4.2 в,г) методичного |
|||||
посібника [15] або за рис. 8.33 [5]. |
|
||||||
Коефіцієнт |
K FV |
- приймають за табл. 3.9 [15] або за табл. 8.3 [5] з |
|||||
пониженням точності на один ступінь проти фактичного. |
|
||||||
Зведений радіус |
ρзв |
кривини в різних перерізах |
прямозубих зубців |
||||
конічного колеса пропорційний початковим (ділильним) діаметрам цих перерізів або відстані від вершини початкового (ділильного) конуса (формула для визначення ρзв не приведена, див. [1] або [5]).
Оскільки питоме навантаження q також пропорційне цим параметрам, то відношення q ρзв постійне для всіх перерізів зубців. При цьому постійними
залишаються і контактні напруження σ H по всій довжині зуба, що дозволяє виконувати розрахунок за будь-яким перерізом (у даному випадку, за середнім перерізом).
Тоді питоме розрахункове навантаження для розрахунку на контактну
міцність
|
q |
max |
+ q |
min |
|
F |
× K |
H |
|
2T2 |
× |
K H |
× K HV |
|
|
q = |
|
|
= |
t |
|
= |
|
|
β |
|
, |
(10.59) |
|||
|
|
2 |
|
b × cosα |
dm2 × b cosα |
||||||||||
|
|
|
|
|
|
|
|
||||||||
де K H = K Hβ × K HV - коефіцієнт навантаження.
225

Коефіцієнт K Hβ приймають за графіком (рис. 4.2 а, б) методичного посібника [15] або за рис. 8.33 [5].
Коефіцієнт K HV - за табл. 3.7 посібника [15] або за табл. 8.3 [5] з пониженням точності на один ступінь проти фактичного.
Розрахунок зубців конічних зубчастих передач
на втому і міцність при згині
Як було показано раніше, профіль зуба конічного колеса в середньому перерізі відповідає профілю зуба еквівалентного прямозубого колеса.
На цій підставі конічні зубчасті колеса на практиці звичайно розраховують на міцність зуба згину за середнім перерізом, аналогічно розрахунку прямозубих циліндричних коліс з урахуванням вищерозглянутих особливостей геометрії конічних передач.
|
Перевірний розрахунок на згин виконують за формулою: |
|
||||||||||||
|
σ |
|
= |
|
Ft × K Fβ × K FV × K Fα |
Y |
×Y |
£ [σ ] , |
|
(10.60) |
||||
|
|
|
|
|
||||||||||
|
|
F |
|
|
υF × b × mm |
|
|
|
F |
β |
F |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
де колову силу |
Ft на ділильному колі в середньому перерізі визначають за |
|||||||||||||
формулою: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ft = |
2T2 |
|
|
; |
|
|
|
(10.61) |
|
|
|
|
|
|
mm × |
|
|
|
|
|
||||
|
|
|
|
|
|
Z2 |
|
|
|
|
||||
для |
конічних |
передач з прямими |
|
зубцями |
беруть коефіцієнти: υF =0,85; |
|||||||||
K Fα =1; Yβ =1; за графіком (рис. 4.3) методичний посібник [15] залежно від |
||||||||||||||
еквівалентних |
чисел зубців шестірні і колеса, визначених за формулою |
|||||||||||||
Z |
= Z |
|
визначають коефіцієнти форми зубців Y |
і Y |
для шестірні і |
|||||||||
V |
cos δ |
|
|
|
|
|
|
|
|
|
F 1 |
F 2 |
|
|
колеса. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Проектний розрахунок. Аналогічно розрахунку циліндричної |
|||||||||||||
прямозубої передачі [див. формулу (10.3)] середній |
модуль |
mm зубців |
||||||||||||
визначається за формулою: |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
226 |
|
|
|
|||

|
|
|
10 |
3 T K |
Fβ |
Y |
F |
|
|
|
mm = K m |
υ × u |
2 |
|
, |
(10.62) |
|||||
× Z 2 ×ψ |
|
|
[σ ] |
|||||||
|
3 |
F |
|
1 |
|
bd |
F |
|
||
|
|
|
|
|
|
|||||
де Km - допоміжний коефіцієнт, для сталевих прямозубих конічних коліс
приймають Km =1,45;
ψ bd |
= |
b |
- коефіцієнт ширини вінця шестірні по відношенню до середнього |
|||||
|
|
d1 |
|
|
|
|
|
|
ділильного |
діаметра, приймають |
ψ bd =0,3…0,6 |
при |
виконанні |
умови |
|||
ψ bR |
= |
b |
≤0,3 і b >10 me ; T2 - |
крутний момент на |
колесі, Нм; |
υF - |
||
e |
|
Re |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
дослідний коефіцієнт, для прямозубих коліс υF =0,85. |
|
|
|
|
||||
|
Розрахунок ведуть по меншому із відношень |
[σ ]F |
Y |
для шестірні і |
||||
|
|
|||||||
|
|
|
|
|
|
F |
|
|
колеса. |
|
|
|
|
|
|
|
|
Перевірний розрахунок на міцність при перевантаженнях виконується аналогічно, як і для прямозубих передач [див. формулу (10.5)].
Розрахунок зубців конічних зубчастих передач на
контактну втому і міцність
В основу розрахунку береться формула Герца для стиснутих циліндрів. Якщо в неї підставити радіуси кривини евольвентних поверхонь зубців у полюсі зачеплення в середньому перерізі у вигляді функції, наприклад, від середнього діаметра dm , одержимо формулу перевірного розрахунку на
контактну міцність:
|
|
2T K |
Hα |
× K |
Hβ |
× K |
HV |
u2 + 1 |
£ [σ ]H |
|
|||
|
2 |
|
|
|
|
|
|
|
|||||
σ H = ZM × ZH × Zε |
|
|
|
|
|
|
|
|
|
|
(10.63) |
||
|
|
|
υH × b |
|
2 |
|
|
|
|||||
|
|
|
|
|
× dm2 |
|
|
|
|
|
|||
де T2 - |
крутний момент на колесі, |
Н·мм; |
K Hα |
- |
коефіцієнт, |
що враховує |
|||||||
розподіл |
навантаження |
між |
зубцями; K HV |
- |
|
коефіцієнт |
динамічного |
||||||
навантаження; υH - дослідний коефіцієнт, |
що враховує зменшення несучої |
||||||||||||
|
|
|
|
|
|
|
|
227 |
|
|
|
|
|

здатності конічної передачі порівняно з еквівалентною передачею, для прямозубої передачі υH =0,85; b - ширина колеса, мм; dm2 - середній діаметр колеса, мм; u - передатне число.
Коефіцієнти ZM і Z H вибирають аналогічно, |
як при |
розрахунку |
||||||||||||||
циліндричних прямозубих передач [15]. |
|
|
|
|
|
|
|
|
||||||||
Коефіцієнт Zε розраховують за |
формулою |
(3.49) |
[15], де |
коефіцієнт |
||||||||||||
перекриття конічної прямозубої передачі визначають за формулою |
|
|||||||||||||||
|
|
|
|
|
|
|
1 |
|
1 |
|
|
|
|
|
|
|
|
|
ε |
α |
= 1,88 - 3,2 |
|
|
+ |
|
|
|
|
|
|
(10.64) |
||
|
|
Z |
|
Z |
|
|
|
|
||||||||
|
|
|
|
|
|
V1 |
|
|
, |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
V2 |
|
|
|
|
|
|
|
де ZV |
і ZV |
- |
еквівалентні |
числа |
зубців |
|
відповідно |
шестірні і колеса, |
||||||||
1 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
визначені за формулою Z |
= Z |
cosδ |
. |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
V |
|
|
|
|
|
|
|
|
|
|
||
Для прямозубої передачі |
K Hα =1; K Hβ |
|
- уточнюють за графіком (див. |
|||||||||||||
рис. 4.2) [15] після уточнення параметра |
ψbR |
u |
|
|
; коефіцієнт K HV |
|||||||||||
|
e |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
(2 |
-ψbR |
) |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e |
|
|
визначають за табл. 3.1 за ступенем точності, на одиницю грубшим, ніж прийнятий за табл. 3.6 [15]. Для прямозубих конічних передач υH =0,85.
Примітка. Спрощений перевірний розрахунок при середніх величинах
коефіцієнтів ZM , Z H і Zε виконують за формулою:
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
σ H = |
335 T K |
× K |
|
(u |
2 + 1)3 |
|
|
£ σ |
H , |
|
||||
|
|
|
2 Hα |
|
HV |
|
2 |
|
|
|
|
|||
|
|
|
|
|
|
|
|
[ |
] |
(10.65) |
||||
|
Rm |
υH × b × u |
|
|
||||||||||
|
|
|
|
|
|
|
|
|||||||
де T2 - крутний момент, Н·мм; Rm - середня конусна відстань, мм; b - ширина колеса, мм.
228
|
Проектний розрахунок на контактну міцність |
|
|||||
Замінивши |
у формулі (10.63) |
значення dm 2 |
= de 2 (1 −0 ,5ψbR |
), |
|||
|
|
|
|
|
|
|
e |
|
|
|
|
|
|
|
|
|
0 ,5de 2 |
|
1 + u2 |
|
|
|
|
b = Re ×ψbdR = |
|
|
|
ψbdR |
і розв'язавши |
одержаний вираз |
|
|
u |
|
|||||
e |
|
|
e |
|
|
|
|
|
|
|
|
|
|
||
відносно de 2 , одержимо формулу для проектного розрахунку конічних
зубчастих передач:
|
|
|
|
|
|
|
|
|
||
de2 = Kd 3 |
|
T2 |
× K Hβ × u |
|
|
|
|
|||
([σ] |
)2 |
× |
(1 -ψ |
bR |
)×ψ |
, |
(10.66) |
|||
|
|
H |
|
|
|
|
bR |
|
||
|
|
|
|
|
|
e |
|
e |
|
|
де Kd - допоміжний коефіцієнт; |
T2 - крутний момент на колесі, Н·м; K Hβ - |
|||||||||
коефіцієнт, що враховує нерівномірність розподілу навантаження по ширині
вінця; u - попереднє значення передатного числа; |
[σ]H - попереднє значення |
||||
допустимого контактного |
напруження, |
МПа; ψbR |
- коефіцієнт ширини |
||
|
|
|
|
e |
|
зубчастого вінця. |
|
|
|
|
|
Для прямозубих передач Kd =1000; для передач з круговими зубцями |
|||||
Kd =890. |
|
|
|
|
|
Коефіцієнт ψbR |
= b |
=0,2…0,3, |
де Re - |
зовнішня конусна відстань. |
|
e |
|
Re |
|
|
|
|
|
|
|
|
|
Більші значення ψbR |
беруть при u ≤3. За рекомендацією ДСТУ ISO 10300 – |
||||
e |
|
|
|
|
|
1,2: 2001 для попереднього розрахунку ψbR =0,285. |
|
|
|||
|
|
|
e |
|
|
Коефіцієнт K Hβ |
обирають залежно від параметру ψbRe × u (2 -ψbR ) за |
||||
|
|
|
|
|
e |
графіком (рис. 4.2) [15].
Перевірний розрахунок на контактну міцність для попередження пластичних деформацій або крихкого руйнування поверхонь зубців виконується аналогічно, як і для прямозубих циліндричних передач [див. формулу (3.30)] у посібнику [15].
229
