Свойства скалярного произведения.

1) Коммутативность: .

Действительно, (т.к. , т.е. четная функция, то ) .

2) Скалярное произведение двух векторов равно длине одного вектора умноженной на проекцию другого на направление первого.

Действительно, .

Отсюда видно, что если , то .

Следовательно, проекция вектора на ось равна скалярному произведению этого вектора на направляющий вектор оси.

3) .

Действительно,

.

4) .

Действительно, .

5) Для того, что бы два ненулевых вектора были перпендикулярны, необходимо и достаточно, чтобы их скалярное произведение было равно нулю.

Пусть     .

Пусть  , т.к. ,    .

6) Пусть  , т.е.  скалярный квадрат вектора равен квадрату длины вектора  .

Тогда

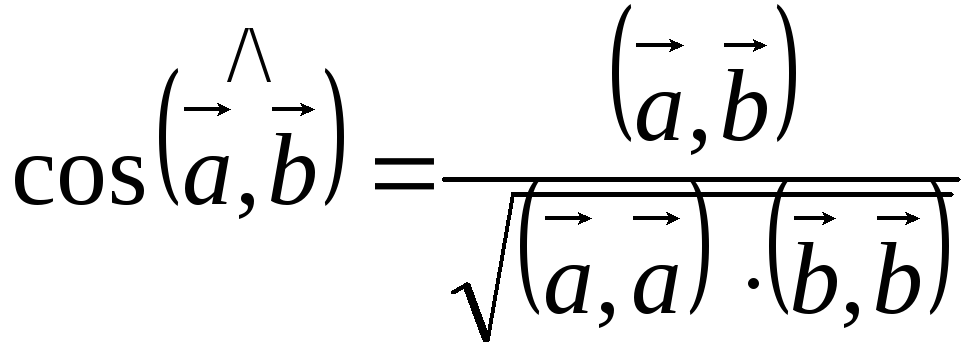
Вычисление скалярного произведения в прямоугольных координатах.

Пусть , .

(, ).

В прямоугольной декартовой системе координат скалярное произведение векторов равно сумме произведений соответствующих координат.

Некоторые метрические формулы.

1)  

2) ,   .

3. Если , то , , .

Т.о., прямоугольные координаты вектора есть его ортогональные проекции на оси прямоугольной системы координат.

4) Пусть ,  .

Таким образом,   .

Из формулы косинуса угла между векторами легко найти углы , , , которые вектор образует с осями координат. Эти углы называются направляющими углами.

Имеем:

, , .

, , называются направляющими косинусами вектора . Они связаны соотношением

.

Следовательно, вектор есть координаты вектора , т.е. вектора и .

.

5^о. Векторное произведение векторов

Пусть даны два неколлинеарных и не нулевых вектора и .

Определение 1. Векторным произведением векторов и называется вектор , удовлетворяющий свойствам:

1. .

2.  и .

3. тройка векторов , , – правая.

Если один из векторов нулевой, или вектора коллинеарны, то их векторное произведение равно нулю.

Построение вектора векторного произведения.

Пусть необходимо построить вектор . Для этого выберем в пространстве точку и отложим из нее вектора и .

1. Через точку проведем плоскость .

2. Спроецируем на П точку . Получим вектор .

3. Далее повернем вектор по часовой стрелке на угол /2 (если смотреть из конца вектора ) и получим вектор .

4. Умножив его на длину, получим , который равен .

Докажем это:

1. .

2. Очевидно, что и .

3. Легко видеть, что тройка , , – правая.

Свойства векторного произведения.

1. Векторное произведение двух не нулевых векторов равно нулю  вектора–сомножители коллинеарны.

Доказательство:

Пусть и   т.к. ,   , т.е. ||.

Пусть ||, тогда   .

2. Длина векторного произведения численно равна площади параллелограмма, построенного на перемножаемых векторах.

Доказательство:

Пусть и . На отрезках [OA] и [OB] построим параллелограмм.

.

3. Векторное произведение антикоммутативно, т.е. .

Доказательство:

Легко видеть, что , т.к. вектора , , образуют правую тройку, то тройка , , – левая  т.е. вектора и – противоположно направлены. Следовательно, .

4. .

Докажем первое равенство.

1. В начале покажем равенство модулей.

т.к. , то .

.

1. Так как ||, то .

1. Покажем, что . Рассмотрим случай и .

Отсюда вытекает доказываемое свойство.

6. – дистрибутивность.

Если один из векторов нулевой – очевидно. Пусть , , – не нулевые. Для доказательства воспользуемся описанным ранее методом построения векторного произведения.

Выберем произвольную точку и отложим из нее вектора и . Из конца вектора построим вектор . Т.о., , , , .

1. Построим плоскость П.

2. Спроецируем на плоскость П: получим .

3. Повернем по часовой стрелке на угол .

4. Умножим отрезки сторон на , получим треугольник подобный .

По построению, , ,  т.к. ), то .