Коэффициент ранговой корреляции Спирмена.

Рассмотрим задачу о силе связи двух различных оценок. Эти 2 оценки были получены вследствие оценивания одного и того же множества объектов по двум различным признакам (критериям). Например, яблоки могут быть оценены по вкусу и по цвету. Или, например, при сертификации учителей начальной школы по уровню квалификации. Их оценка может проводиться по двум признакам:

1) по формальным тестам;

2) по мнению руководства школы.

Обозначим соответственно первый признак как , а второй как.

Тогда результаты оценивания можно представить в виде таблицы:

, где - значение ранга, присвоенного объекту с номером по признаку , гдепринимает значение 1 и 2.

Требуется определить силу связи этих двух оценок. Необходимо ввести меру, значения которой лежали бы в отрезке , и которая была бы равна:

1. "1", если связь сильная положительная,

2. "-1", если связь сильная отрицательная,

3. "0", в случае отсутствия связи.

Связь будет идеально положительной, если значение для, и, идеально отрицательной, если(т.е., если при упорядочивании таблицы по первой строке, вторая строка будет упорядочена в обратном порядке). В качестве такой меры выступаеткоэффициентом ранговой корреляции Спирмена. Обозначается: .

Коэффициент корреляции Спирмена - это аналог коэффициента корреляции Пирсона, но подсчитанный для ранговых переменных, вычисляется он по следующей формуле: , которая получается путем алгебраических преобразований формулы для подсчета коэффициента Пирсона.

Из данной формулы видно, что коэффициент корреляции Спирмена полностью удовлетворяет требованиям к мере оценки, сформулированным выше. В отличие от коэффициента корреляции Пирсона, в значении коэффициента корреляции Спирмена значимыми являются только 3 знака после запятой.

Определенная выше формула коэффициента корреляции Спирмена справедлива, в случае, когда нет распределенных рангов. Если же они есть, то формула усложняется.

Коэффициент "" Кендалла

Снова рассмотрим оценивание одного и того же множества объектов по

д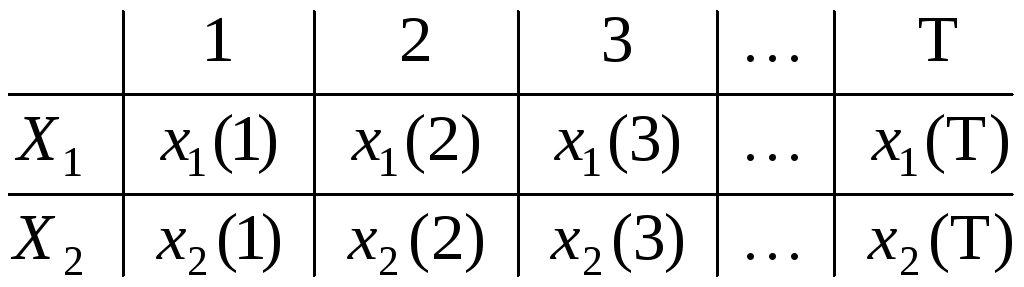вум признакам: и.Задача: определить силу связи между оценками. Использование коэффициента корреляции Спирмена было бы правильным решением данной задачи, однако, оно имеет недостаток. При вычислении мы должны были находить разность между значениями рангов, но в ряде случаев эта операция бессмысленна (например, разность между 1-м и 2-м местами на соревнованиях не соответствует разности между 16-м и 17-м местами).

Этого недостатка лишен коэффициент ранговой корреляции Кендалла ("" Кендалла). Он отвечает всем свойствам меры связи двух оценок, сформулированных выше для коэффициента корреляции Спирмена, и опирается на идею согласованных и несогласованных пар.

Два объекта называются:

• согласованными, если

• несогласованными, если

.

Здесь и далее мы считаем, что в наших ранжированных рядах оценок нет распределенных рангов.

Если между иесть идеальная положительная связь, то все пары согласованны. Соответственно, если междуиесть идеально отрицательная связь, то все пары несогласованны.

Если связи нет, то количество согласованных и несогласованных пар должно быть одинаково. На этой идее построена статистика Кендалла. Для ее вычисления используются индикаторы:

Тогда получим следующие эквивалентные варианты вычислений.

1). Для .

- это точное значение,

т.е. доля согласованных пар минус доля несогласованных. Оценка:

Если все пары согласованы, то . Если же все пары несогласованны, то.

2). Для .- точное значение.

Оценка: .

3). Для .- точное значение.

Оценка: .

i=1,2

m_i –число групп

число элементов в группе

При анализе силы связи мы двигаемся от простых ситуаций (числовых данных) к сложным (когда данные не имеют числовых значений). В этом разделе мы сталкиваемся с категориальными (номинальными) переменными, для которых выполняются:

1) они имеют конечное число значений; 2) для их значений не определено отношение порядка.

Задача 1. Пусть у нас имеется лекарство, и мы хотим проверить, есть ли связь между приемом этого лекарства и состоянием больного (ухудшение или улучшение состояния). Больных случайным образом делят на две неравные группы. Первую группу лечат новым препаратом, а вторую группу лечат традиционными методами. Таким образом, мы получаем два показателя:

1.Проходил ли больной курс лечения новым лекарством.()

A – давали лекарство

–не давали лекарство.

2.Результат лечения ().

В – состояние улучшилось

–состояние ухудшилось.

	В
А
			N

n₁₁ – число пациентов, принимавших лекарство, чье состояние улучшилось,

n₁₂ – число пациентов, принимавших лекарство, чье состояние ухудшилось,

n₂₁ – число пациентов, не принимавших лекарство, чье состояние улучшилось,

n₁₁ - число пациентов, не принимавших лекарство, чье состояние ухудшилось.

По четырем приведенным числам необходимо сказать, связан ли результат лечения с приемом лекарства и как именно связан.

Если между инет никакой связи, тогда доля принимавших лекарства среди больных, чье состояние улучшилось должна быть равна доле принимавших лекарство, среди тех, кому стало хуже, и равна доле принимавших лекарство среди всех больных.

Верно, следовательно, доля принимавших лекарство, среди тех, чье состояние улучшилось:

Доля принимавших лекарство, чье состояние ухудшилось:

Доля тех, кто принимал лекарства, среди всех, участвовавших в эксперименте:

- признак отсутствия связи.

На равенстве долей построена мера связи. В основу меры силы связи можно положить разность вида:

- но у этой величины значения могут быть больше или меньше единицы по модулю, следовательно, необходимо ее модифицировать, чтобы сделать похожей на коэффициент корреляции.

- Коэффициент Юла

Будем говорить, что между признаком и существует максимальная положительная связь, если из наличия будет обязательно следовать(не лечат, следовательно, стало хуже).

Таким образом, таблица имеет вид:

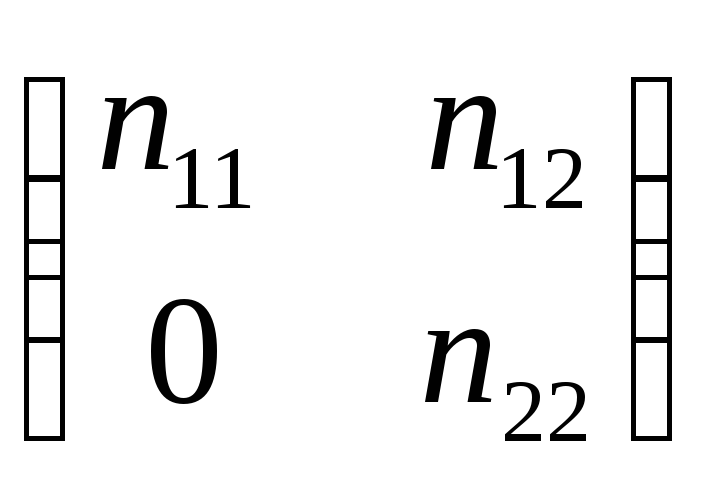то есть признаком максимальной положительной связи является n₂₁=0.

Между признаками существует максимальная отрицательная связь, когда из следует(если не лечили, то обязательно стало лучше).

таким образом n₂₂=0.

При максимальной положительной связи D = 1

При максимальной отрицательной связи D = -1

Все остальные ситуации дают значение в промежутке [-1, 1]. Таким образом, коэффициент D является аналогом коэффициента корреляции.

Наши наблюдения могут рассматриваться, как реализации случайных величин. Значит, значение коэффициента Юла может рассматриваться тоже как реализация случайной величины, и существует возможность оценить значимость этого значения, например, с помощью "стандартной ошибки".

Стандартная ошибка:. Используя свойство асимптотической нормальности, мы можем проверить равенство нулю истинного значения коэффициента Юла.

Однако проверка значимости силы связи чаще осуществляется по-другому.